钢轨断缝可按式（3-16）检算。

式中 λ—— 钢轨断缝（mm）；

ΔTdmax —— 最大降温幅度（ °C），ΔTdmax=Tu -Tmin ；

r —— 线路纵向阻力[kN/（m·轨）]；

[]λ—— 钢轨断缝容许值（mm），取70 mm。根据式（3-16），分别计算钢轨降温40 °C、50 °C、60 °C和70 °C条件下的断缝值，并将理论计算结果与本书计算结果进行对比，如表3-23所示。(www.daowen.com)

表3-23　钢轨断缝值计算结果

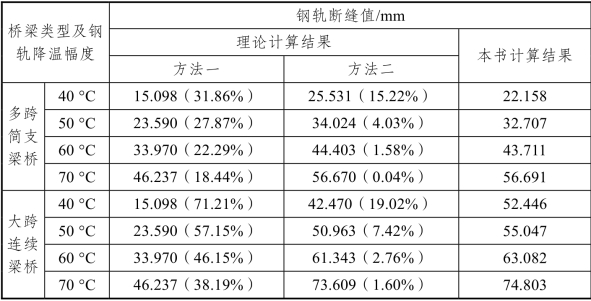
注：1. 表中，“（）”内百分比为理论计算结果与本书计算结果的相对误差。
2. 结合本书 3.1 节计算结果，多跨简支梁桥和大跨连续梁桥上钢轨最大伸缩力分别为214.40 kN和620.94 kN，方法一不考虑桥上无缝线路伸缩力的影响，线路阻力取无载条件下扣件纵向阻力最大值；方法二考虑桥上无缝线路伸缩力的影响，线路阻力取无载条件下扣件纵向阻力，并考虑其纵向阻力非线性的变化。

由表3-23可知，钢轨在降温60 °C条件下发生断轨时，采用理论公式（方法一）计算得多跨简支梁桥和大跨连续梁桥上钢轨断缝值平均值都是34.0 mm，分别仅为本书有限元模型计算结果的77.7%和53.9%，这是由于公式法未考虑伸缩附加力的影响，从而大大低估了断缝扩展程度。在充分考虑桥上无缝线路伸缩力的影响及扣件纵向阻力的非线性变化后（方法二），钢轨断缝值的计算结果与本书计算结果更为接近。就本书所建立的模型而言，多跨简支梁桥上钢轨断缝值未超出限值，且有很大的安全冗余，大跨连续梁桥上钢轨断缝值在钢轨降温幅度小于或等于60 °C范围内未超出安全限值。

对于桥上CRTSⅢ型板式无砟轨道无缝线路，采用理论公式法计算钢轨断缝值会大大低估断缝的扩展程度，无法满足工程需求，因此，需要充分考虑桥上无缝线路伸缩力的影响，并建议考虑扣件纵向阻力的非线性变化，采用梁-板-轨相互作用法建立的空间耦合模型进行精确计算。