钢轨强度允许温降按式（3-6）计算。

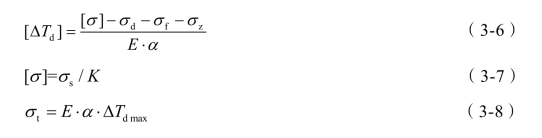
式中 [σ]—— 钢轨容许应力（MPa）；

σd—— 钢轨动弯应力（MPa）；

σf—— 钢轨最大附加应力（MPa）；

σz—— 钢轨牵引（制动）应力（MPa）；

E—— 钢轨钢弹性模量，取2.058×105 MPa；

α—— 钢轨钢线膨胀系数，取1.18×10-5/°C；

σs—— 钢轨钢屈服强度（MPa），CHN60（U71Mnk）钢轨屈服强度为457 MPa；

K—— 安全系数，取1.3；

σt—— 钢轨最大温度应力（MPa）；

ΔTd max—— 无缝线路最大降温幅度（ °C）；

Pf— — 桥上无缝线路钢轨附加纵向力（N）；

F—— 钢轨断面面积（mm2），CHN60钢轨断面面积为77.45 cm2。根据式（3-6）～式（3-9），钢轨强度应满足式（3-10）。

钢轨基础弹性模量（表示单位长度钢轨基础的弹性特征），按式（3-11）计算。

式中 u—— 钢轨基础弹性模量；

D —— 钢轨支点刚度，对于无砟轨道主要取决于轨下胶垫刚度，计算时可取轨下垫板刚度，WJ-8型扣件轨下垫板刚度取35 kN/mm；

a —— 扣件节点间距，取0.63 m。

在静轮系作用下，钢轨静弯矩M0按式（3-12）计算。

式中 M0—— 钢轨静弯矩；

k —— 钢轨基础与钢轨的刚比系数；(www.daowen.com)

EIx—— 钢轨钢的弹性模量（取2.058×105 MPa）和钢轨截面对其水平中性轴的惯性矩（CHN60钢轨取32 170 000 mm4）的乘积，则k=0.001 204（mm-1）；

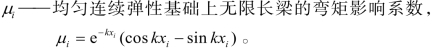
以CRH2型动车组为例，最大轴重为14 t，单个转向架固定轴距为2 500 mm，选取单个转向架一侧车轮最为计算轮系，计算得钢轨静弯矩为

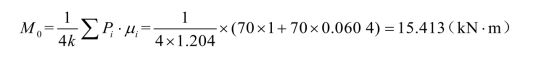
钢轨动弯矩Md按式（3-13）计算。

式中 Md—— 钢轨动弯矩（kN·m）；

α—— 速度系数，速度大于160 km/h时取1.0；

β—— 偏载系数，直线段取0。

钢轨边缘的最大动弯应力和按式（3-14）和式（3-15）计算。

式中 σ头d，σ底d—— 轨头外缘最大动压应力和轨底外缘最大动拉应力（MPa）；

W头，W底—— 钢轨头部和底部对其水平中和轴的截面系数（mm3），CHN60钢轨的W头，W底分别为339 400 mm3和396 000 mm3；

f —— 轨道横向水平力系数，直线段取1.25。

根据上式，计算得轨头压应力和轨底拉应力分别为113.53 MPa和97.30 MPa。根据本章3.1节～3.3节计算结果，桥上CRTSⅢ型板式无砟轨道无缝线路最大纵向力如表3-20所示。

表3-20　钢轨纵向力最大值

由表3-20可知：相比于伸缩力与制动力，钢轨附加挠曲力很小，因此，在检算过程中可不考虑钢轨挠曲力；钢轨伸缩力和钢轨制动力分别是在升温荷载和全桥列车朝向活动端制动荷载条件下计算的，且降温荷载与升温荷载作用下的钢轨最大纵向力大小相等、方向相反，全桥列车朝向活动端和朝向固定端制动荷载作用下的钢轨最大纵向力也是大小相等、方向相反。因此，在检算时钢轨伸缩力与制动力的大小可分别取绝对最大值，即多跨简支梁桥上钢轨最大附加（伸缩+制动）压力/拉力均为451.79 kN，大跨连续梁桥上钢轨最大附加（伸缩+制动）压力/拉力均为872.37 kN。

因为无砟轨道横向阻力较大，横向稳定性较好，所以无砟轨道无缝线路钢轨强度检算一般以抗拉强度作为检算标准。将上述计算结果分别依次代入式（3-6）～式（3-10）可知：全桥采用WJ-8型常阻力扣件的铺设方案条件下依据钢轨强度所确定的轨温变化允许值如表3-21所示；钢轨降温幅度分别为30 °C、40 °C、50 °C和60 °C条件下，依据钢轨强度所确定的钢轨最大伸缩力和制动力之和的允许值如表3-22所示。

表3-21　轨温变化允许值

表3-22　钢轨（伸缩+制动）力允许值

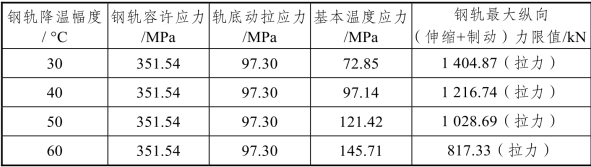
由表3-21和表3-22可知，对于桥上CRTSⅢ型板式无砟轨道无缝线路，混凝土梁年温差为20 °C条件下，就本书所建立的模型而言，多跨简支梁桥和大跨连续梁桥上全桥采用WJ-8型常阻力扣件的铺设方案分别适用于钢轨降温幅度小于80.67 °C和58.31 °C的地区；在轨温降温幅度分别为30 °C、40 °C、50 °C和60 °C的地区，钢轨最大（伸缩+制动）力绝对值分别不得高于1 404.87 kN、1 216.74 kN、1 028.69 kN和817.33 kN，并应以该值作为控制指标来选取无缝线路最优铺设方案。