1．静力计算结果对比

现阶段关于桥上CRTSⅢ型板式无砟轨道的研究成果还较少，又由于桥上CRTSⅠ型板式无砟轨道所采用的WJ-7型扣件和桥上CRTSⅢ型板式无砟轨道所采用的WJ-8型扣件阻力大小一致，且两种板式无砟轨道的扣件间距分别为0.629 m和0.630 m，这两种单元板式无砟轨道应用于桥上时其梁-板-轨相互作用机理具有相似性，钢轨纵向力、位移分布规律及其峰值也基本一致。文献[154]中通过建立空间耦合模型，分析了伸缩力工况下桥上CRTSⅠ型板式无砟轨道无缝线路纵向力分布，本书建立了与文献[154]相同桥跨的空间耦合模型，如图2-14所示。扣件纵向阻力分别考虑15 kN/组和4 kN/组两种工况，相同温度荷载作用下的钢轨纵向力与位移对比分别如图2-15和图2-16所示，钢轨纵向力、纵向位移及梁体纵向位移最大值对比如表2-5所示。

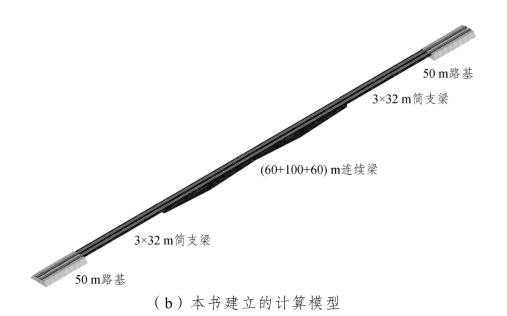
图2-14　空间耦合模型对比

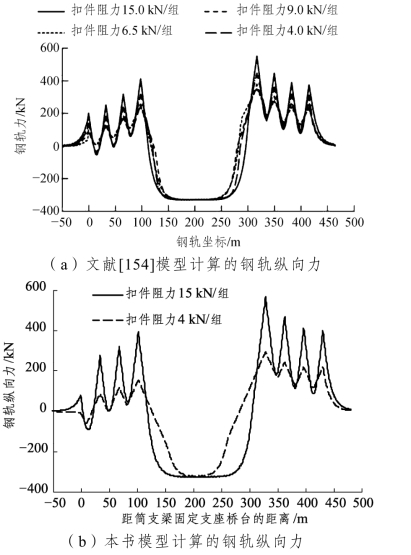
图2-15　钢轨纵向力计算结果对比

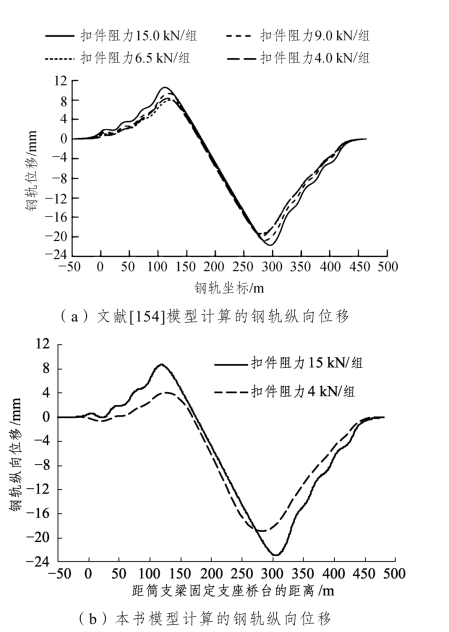
图2-16　钢轨纵向位移计算结果对比

表2-5　结构纵向力与位移计算结果对比

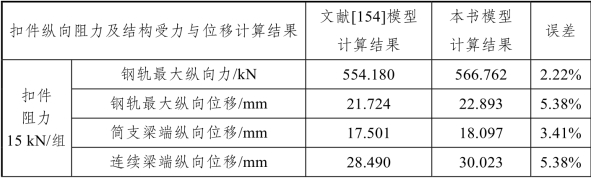
续表(www.daowen.com)

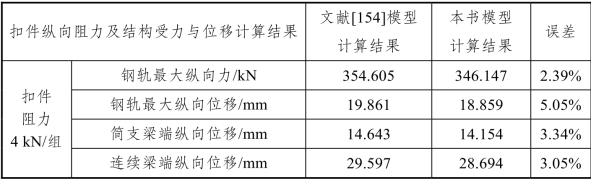
从图2-15、图2-16及表2-5可以看出：相同工况下，文献[154]中的钢轨纵向力、纵向位移分布规律与本书模型的计算结果均一致，且钢轨纵向力、纵向位移、简支梁及连续梁端纵向位移最大值基本相同，最大误差仅为5.38%。考虑到CRTSⅠ型和CRTSⅢ型板式无砟轨道结构尺寸及力学特性上存在一定差异，误差在可接受范围内。

2. 动力计算结果对比

西南交通大学翟婉明院士在其专著《列车-轨道-桥梁动力相互作用理论与工程应用》[155]中，建立了双线10×32 m简支梁桥有限元模型，分析了高速列车以速度250 km/h通过第5跨时该跨轨道及桥梁结构的动力响应特征。本书建立了相同桥跨的计算模型，在相同工况下与其对比钢轨、桥梁梁体及墩顶位移响应，并定义结构竖向位移以向上为正方向，其计算结果分别如图2-17和图2-18所示。

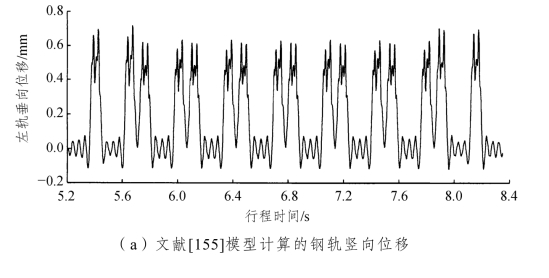
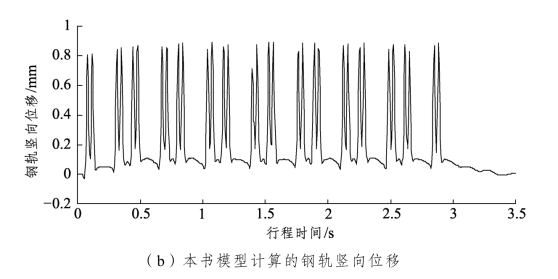
图2-17　钢轨竖向位移计算结果对比

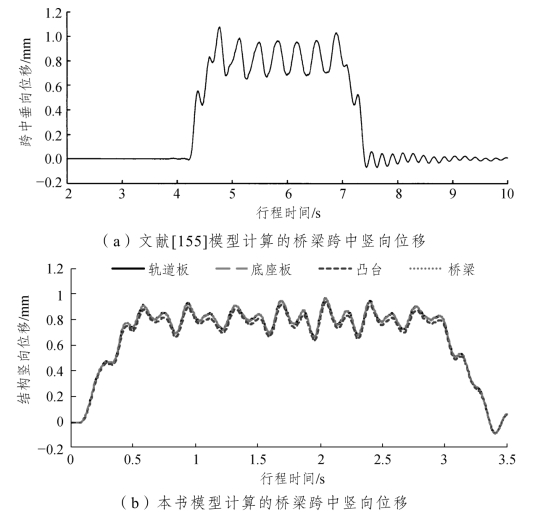
图2-18　桥梁跨中竖向位移对比

从图2-17和图2-18可以看出：相同工况下，文献[155]中的钢轨和桥梁跨中竖向位移响应规律及其峰值与本书模型的计算结果基本一致。

通过本书与已有文献的静力、动力计算结果对比，验证了本书所编制的桥上CRTSⅢ型板式无砟轨道无缝线路纵向力计算程序及其建立的空间耦合模型的通用性和可靠性。故本程序可用于桥上CRTSⅢ型板式无砟轨道无缝线路纵向静力和动力分析。