根据CRTSⅢ型板式无砟轨道结构组成及其在桥上分块铺设的施工方式，桥上CRTSⅢ型板式无砟轨道无缝线路纵向力传递是建立在梁-板-轨相互作用基础之上的，如图2-1所示。其中，梁、板、轨之间的纵向相互作用力包括：梁体发生伸缩和挠曲变形受到上部结构约束而产生的伸缩附加力和挠曲附加力；列车制动荷载引起的制动附加力；钢轨在低温下折断形成的断轨力。

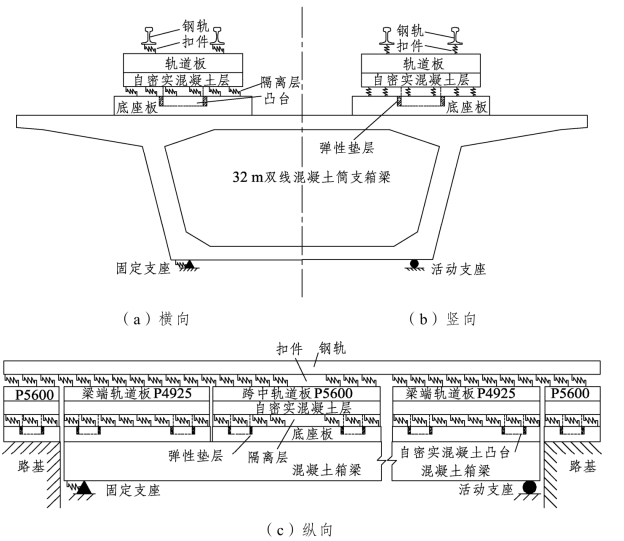
图2-1　桥上CRTSⅢ型板式无砟轨道无缝线路梁-板-轨相互作用示意图

对于轨道层间的纵向约束，桥梁和底座板通过施工前桥面板凿毛处理和预埋钢筋使两者固结，可不考虑底座板与桥梁之间的相对位移；底座板与自密实混凝土层间约束包括隔离层的摩阻力作用，以及底座板凹槽和自密实混凝土层凸台的咬合作用；轨道板下预留的门形筋与灌注的自密实混凝土固结，可不考虑轨道板与自密实混凝土层间的相对位移；钢轨与轨道板间纵向阻力即为使两者联结的扣件纵向阻力。

桥梁梁体由于温度变化发生伸缩变形，或在列车竖向荷载作用下发生挠曲变形，都会自下而上地通过轨道层间阻力对上部钢轨产生附加伸缩力和附加挠曲力；与之不同的是，当列车在桥上制动时，纵向轮轨力则是通过轨道层间阻力自上而下地依次传递至下部轨道及桥梁结构。低温条件下发生断轨，折断的钢轨在断口处急剧收缩，该处钢轨温度力瞬间得到释放并通过层间阻力自上而下地传递至下部轨道及桥梁结构，并对固定支座墩/台顶产生断轨力。最终，桥上CRTSⅢ型板式无砟轨道无缝线路在轨道层间约束、墩/台顶固定支座约束和路基段约束的共同作用下，形成一个新的力学平衡体系。

梁-轨相互作用微分方程推导如下：

任意取dx长的微段钢轨分析其受力平衡的条件，如图2-2所示。假设钢轨受拉为正，x坐标向右为正，钢轨位移y与梁体位移Δ均向右为正，则梁-轨相对位移u为

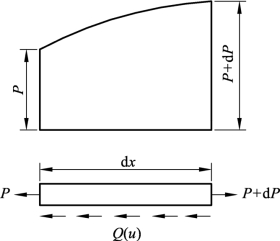
图2-2　钢轨受力示意

图2-2中Q(u)为作用在梁体与钢轨间的纵向分布阻力荷载（也称线路阻力），当u为正值时，Q(u)也为正值，但方向向左。因此，由钢轨受力的平衡条件，可得

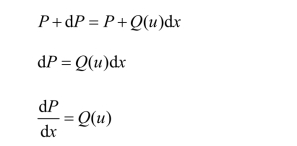
在dx微段范围内，其变形量为(www.daowen.com)

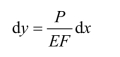
于是可得

即

式中 E—— 钢轨钢弹性模量；

F—— 钢轨断面面积。

由式（2-1）可得

将式（2-2）带入式（2-3），可得