我国桥上无缝线路纵向静力计算方法的发展可分为以下几个阶段[12]。

1. 常阻力迭代求解法

假定桥上长钢轨位于无缝线路固定区，桥梁因伸缩或挠曲变形导致桥上长钢轨产生伸缩或挠曲附加力，再通过假定钢轨发生纵向位移范围为未知量，可对应得到钢轨附加拉压面积之和，用迭代法即可求得拉压面积之和为零时所对应的钢轨发生纵向位移范围。1987年，卢耀荣等[74]假定梁轨相对位移为未知量，建立了相应的非齐次微分方程，并采用龙格-库塔（Runge-Kutta）法进行求解，但由于该方法需先用有限单元法求解梁的位移曲线，在计算长大桥梁时易造成误差积累，所得数据精度较低，一般只用于简化计算。

2. 非线性阻力的微分方程数值解法

20世纪80年代起，我国研究人员开始求微分方程的非线性解，其中包括指数型非线性阻力及分段线性阻力的微分方程数值解法，通常采用欧拉法或四阶龙格-库塔法进行数值积分[75,76]。1990年，杨少宏详细探讨了采用微分方程解法计算挠曲力的思想[77]，并通过对线路纵向阻力分段线性化，将原有的非线性微分方程简化为线性微分方程进行求解。

3. 基于广义变分原理的解析求解法

从梁、轨体系的能量观点出发，基于广义变分原理，将边界条件转变为变分问题，求解梁轨相互作用的平衡方程[78,79]；不过该方法需要预先得知钢轨纵向力的大致分布形状，并假定出合理的形函数，故通用性不强。

4. 有限元数值求解法

有限元法以变分原理为基础，其中包括最小势能原理、最小余能原理和混合变分原理。该方法计算精度高、通用性强，且能适应各种复杂荷载及结构。随着计算机硬件和软件的飞速发展，有限元法得到了广泛的应用，我国桥上无缝线路有限元模型可分为以下几类：

（1）单层阻力模型。

采用带刚臂的刚架模拟桥梁的挠曲变形和纵向位移，采用抗弯杆件、抗拉压杆件或弹簧模拟线路纵向阻力，如图1-9所示。

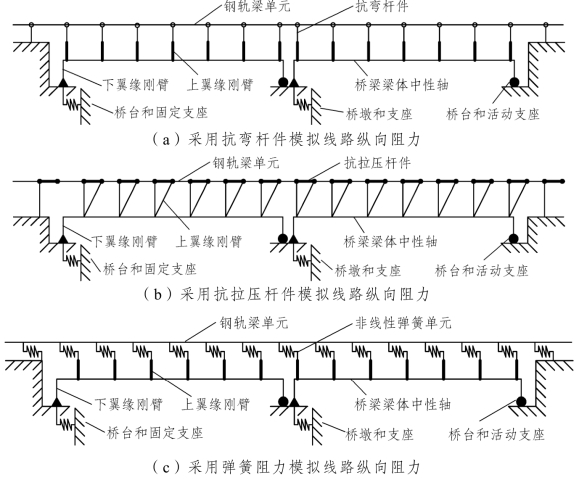
图1-9　单层阻力模型

中南大学闫斌等[80]以哈齐高速铁路上某一（77+3×156.8+77）m系杆拱连续梁桥为例，根据拱肋、横向支撑、吊杆、梁、桥墩及轨道位置之间的相互作用，建立了考虑大跨度系杆拱连续梁桥与多股轨道相互作用的模型，采用钢-混凝土组合截面梁单元模拟钢管混凝土（CFST）拱肋，对该桥上无缝线路的铺设进行了探讨，分析了长钢轨纵向力、墩顶纵向力和不平衡负载情况下的扭矩。

铁道第四勘察设计院（铁四院）李秋义等[81]和李阳春[82]根据梁轨相互作用原理，建立了多跨简支梁桥轨-梁-墩有限元模型，采用单位荷载法计算桥墩温差引起的桥上无缝线路钢轨附加力，探究其分布规律及影响因素，指出桥墩温差引起的钢轨附加力随着桥墩高度和墩顶纵向水平线刚度的增加而增大，而桥梁跨度对桥墩温差引起的钢轨附加力影响较小。

西南交通大学张迅[83]在其硕士学位论文中基于连续梁桥上无缝线路线-桥-墩-基础一体化计算模型，利用APDL语言实现了对ANSYS的二次开发，编制了桥上无缝线路纵向附加力计算程序ALFCWR，分析了桥墩温差荷载引起的连续梁桥上无缝线路纵向力特性[84]。

王平、谢铠泽等提出了简化的连续刚构桥上无缝线路计算模型与方法[85]，分析了刚构桥及相邻简支梁桥桥墩纵向水平刚度匹配关系对制动荷载下梁-轨快速相对位移的影响[86]，结果表明简化的连续刚构桥上无缝线路模型适用于伸缩、断轨及制动工况下的计算，而挠曲工况下的计算必须依据桥梁实际尺寸建立整体变截面梁模型。

蔡敦锦等[87]分析了伸缩力的作用规律及桥梁跨数、支座、墩台纵向水平刚度、桥梁跨度对伸缩力的影响，建议在计算桥上无缝线路伸缩力时，可将多跨简支梁桥简化为10跨，多联连续梁桥两侧简支梁简化为5跨。

徐金辉等[88]分析了某一大跨度双线中承式钢-混凝土结合桁架拱桥上的无缝线路纵向力，指出在对中承式拱桥桥上无缝线路进行检算时，应当考虑拱肋的日温差及挠曲力对拱肋的影响，并建议中承式拱桥的拱肋采用钢管混凝土或钢-混凝土结合桁架结构，以保证拱肋有一定的抗拉强度。

刘婷林等[89]基于梁-轨相互作用原理，采用有限元法建立线-桥-墩一体化模型，计算了纵向、横向温度梯度下桥墩位移对梁轨相互作用的影响，指出在设计桥上无缝线路时需要考虑桥墩纵向温度梯度和梁体整体温差的叠加。

魏贤奎等[90]建立了上承式拱桥上无缝线路断缝计算力学模型，分析了桥梁结构、墩台刚度及股道数等因素对钢轨断缝的影响，指出断缝与拱肋温差近似呈线性关系，且采用公式法会低估钢轨断缝。

中南大学戴公连、闫斌等[91,92]建立了桥塔-缆索-轨道-梁体-桥墩-桩基的斜拉桥有限元模型，探究了斜拉桥上无缝线路纵向力分布规律，并采用非线性弹簧单元模拟轨道和桥梁之间的纵向阻力来建立连续梁桥上轨道-桥梁-桥墩-基础系统一体化有限元模型，比较并研究了分别采用常阻力扣件和小阻力扣件时各工况下桥上无缝线路的纵向力。结果表明：在计算斜拉桥上附加伸缩力和挠曲力时需考虑相邻桥梁的影响，计算时可将相邻简支梁跨简化为6跨；小阻力扣件可有效降低桥上无砟轨道和无缝线路之间的附加力，减少钢轨伸缩调节器的使用。

兰州交通大学孙伟龙等[93]对高寒地区某一钢-混结合梁桥梁轨相互作用规律进行了分析，对在高寒地区钢-混凝土结合梁桥上铺设无缝线路提出了合理化建议。

（2）双层阻力模型。

采用双层非线性弹簧单元分别模拟桥上有砟轨道无缝线路的扣件纵向阻力和道床纵向阻力，如图1-10所示，也可分别模拟CRTSⅠ型板式无砟轨道的扣件纵向阻力和轨道板与CA砂浆层间的摩阻力。

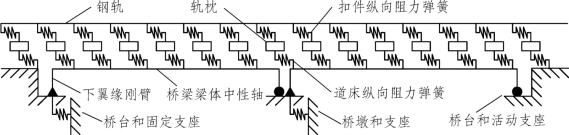
图1-10　双层弹簧阻力模型

西南交通大学陈杨[94]在其硕士学位论文中对简支梁桥上CRTSⅠ型板式无砟轨道纵向静力进行了分析，对比分析了有无凸型挡台对梁-板-轨相互作用的影响，结果表明凸型挡台在一定程度上可以阻止轨道板纵向位移，降低钢轨纵向力，凸台内部纵向受力从台顶往下逐渐减小。

邢梦婷、王平[95]建立了桥上纵连板式无砟轨道无缝线路的线-板-桥-墩一体化计算模型，研究了挠曲力作用下荷载参数变化对梁轨相互作用的影响。

谢铠泽等[96,97]针对刚构桥和连续梁桥上CRTSⅠ型板式无砟轨道，分别建立了两种线-板-桥-墩一体化计算模型，分析了刚构桥梁端轨下垫板窜出、凸台裂缝及凸台周围填充树脂离缝等病害产生的原因。

为探究桥墩在工后沉降及温度梯度荷载作用下所引起的高墩大跨桥上无缝线路梁轨相互作用规律，以新建铁路长沙至昆明客运专线玉屏至昆明段内某一高墩（89+168+89）m连续刚构桥梁+（33+56+33）m连续梁桥为例，基于所建立的线-桥-墩一体化有限元模型，胡志鹏等[98]分析了桥墩不均匀沉降和均匀沉降对钢轨纵向力、线路高低不平顺及墩台受力的影响；张亚爽等[99]分析了高桥墩在纵向、横向温差作用下对桥上长钢轨纵向力的影响，指出在设计高墩大跨桥上无缝线路时需考虑高墩在纵横向温差作用下对桥上无缝线路的影响。

罗华朋等[100,101]以高墩大跨连续刚构桥上CRTSⅠ型板式无砟轨道为研究对象，分别分析了高墩大跨桥墩在整体升温和纵向温度梯度条件下，桥上无砟轨道无缝线路的受力及其平顺性，建议在设计高墩大跨桥上无缝线路时，考虑桥墩升温这种特殊荷载对桥上无缝线路所引起的竖向不平顺，且应考虑梁体升温和桥墩温度梯度最不利的组合来检算墩台刚度。

（3）三层阻力模型。(www.daowen.com)

三层阻力模型多用于桥上CRTSⅡ型板式无砟轨道这种特殊结构，它的层间纵向阻力由上至下分别为钢轨与轨道板之间的扣件、轨道板与底座板之间的CA砂浆层、底座板与梁跨之间的“两布一膜”滑动层，这3层约束均采用非线性弹簧模拟，桥梁采用梁单元或平面单元模拟，如图1-11所示。

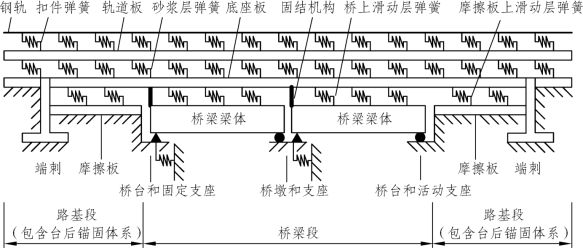
图1-11　三层弹簧阻力模型

针对桥上CRTSⅡ型板式无砟轨道这种特殊结构，朱乾坤等[102]和方利等[103]等采用三层弹簧阻力模型，分析了列车制动荷载作用下的纵向力传递规律及其影响因素，指出在检算时应考虑多种制动荷载位置的影响，“两布一膜”滑动层和固定支座梁端的固结机构在一定程度上可隔离梁-板-轨的相互作用。

西南交通大学吴青松等[104]探究了CRTSⅡ型板式无砟轨道在桥上应用时所能适应的最大温度跨度。

陈嵘等[105]针对简支梁和连续梁桥上CRTSⅡ型板式无砟轨道无缝线路的结构特点，对其梁-轨作用规律进行了较为全面的分析，表明了滑动层摩擦系数对于该种轨道结构的重要性。

刘成等[106]分析了桥上纵连板式无砟轨道墩/台位移引起的作用力，指出在设计中需考虑该因素的影响，且应考虑墩顶位移和梁体伸缩两种荷载的耦合作用。

中南大学戴公连等[107]对桥上无砟轨道的非线性温度模式进行了长期监测，并基于此分析了桥上长钢轨纵向力及纵连的轨道层间的相对位移，建议改进固结机构的作用，指出连续梁固定支座墩顶处的轨道板也需与固结机构相连，在考虑实测温度工况及制挠力耦合作用的基础上，对比了纵连板和单元板式无砟轨道应用于桥上无缝线路时的受力规律及桥梁理论最大温度跨度，并比较制动墩墩顶刚度、扣件阻力等参数对无缝线路受力及最大温度跨度的影响[108]。

（4）空间整体刚臂模型。

考虑两根钢轨与桥梁间的纵向相互作用，钢轨视为杆单元，线路阻力采用杆单元模拟，桥梁采用带多向刚臂的构架模型，桥梁及基础均采用杆单元模拟，如图1-12所示[109,110]。

中南大学戴公连、刘文硕等[111]针对高速铁路提篮拱桥这种复杂的大跨结构，建立了钢轨-纵梁-横梁-吊杆-基础耦合系统的力学模型，研究了提篮拱桥上无缝线路的传递规律，对比分析了纵向阻力模型、纵向约束条件及拱肋内倾斜度等一些敏感因素对纵向力的影响。

闫斌等[112]指出与连续梁相邻的简支梁刚性墩所受的伸缩力非常大，需要特别考虑其刚度设置和支座的选择，减小纵向阻力在使得连续梁上钢轨内部应力减小的同时会使得梁-轨相对位移迅速增大，提出了增大简支梁刚性墩刚度的建议。

徐庆元[113]在其博士学位论文中基于有限元法建立了梁-轨相互作用空间刚臂模型，研究了秦沈客运专线上某多跨简支箱梁桥上有砟轨道长钢轨的纵向受力，进一步考虑了挠曲力计算时的动力效应。

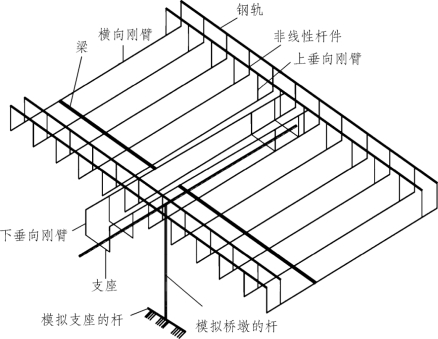
图1-12　空间整体刚臂模型

华东交通大学孔文斌[114]在其硕士学位论文中结合了京沪高铁工程实际，根据某长大无砟轨道桥上无缝线路的梁-轨相互作用原理，对比了桥梁跨数、刚性墩刚度、线路阻力等因素对长钢轨纵向受力的影响。

西南交通大学段翔远等[115,116]建立了考虑桥梁-墩台-基础相互作用的一体化计算模型，研究了高墩大跨连续刚构桥在温度荷载、风荷载等作用下产生的竖向变形、横向变形、纵向变形对无砟轨道的影响，分析了静风荷载对桥梁纵向位移、横向位移的影响，以及不同桥型对静风荷载抵抗能力的影响。研究结果表明，温度变化会使得高墩大跨桥梁产生梁端转角，进而影响该处扣件系统纵连式无砟轨道的受力，由静风荷载产生的桥梁横向位移不会影响无缝线路稳定性，但由于静风荷载而产生的梁体及桥墩纵向位移将会影响梁-轨相互作用；作者通过进一步对比不同桥型对静风荷载的抵抗能力，指出采用刚构桥梁较连续梁桥更有利于控制风荷载对桥梁变形的影响。

5. 空间整体实体模型

随着计算技术的发展，部分学者直接将钢轨、轨枕、桥梁、墩台采用实体单元（或部分为梁单元）来模拟，如图1-13所示。

图1-13　空间整体实体模型

北京交通大学陈鹏[117]在其博士学位论文中采用ANSYS建立了用于无砟轨道设计计算的有限元分析模型，并运用ABAQUS分析了中高速条件下车辆、无砟轨道、路基及桥梁系统的动力响应，对路基及桥梁上无砟轨道系统的动力响应水平进行了较为全面的评价。

北京交通大学曲村[14]在其博士学位论文中考虑高速车辆、无缝线路、无砟轨道和长大桥梁之间的相互作用机理，采用理论和试验相结合的研究方法，分别针对长大桥上CRTSⅠ型、CRTSⅡ型板式和双块式无砟轨道，对其纵向静力特性以及横向、垂向动力特性展开研究，从设计检算的角度对各结构的参数取值提出了合理化的建议[118]。

北京交通大学乔神路[119]在其博士学位论文中自主建立了高速铁路桥上无砟道岔的精细化空间耦合模型，采用以静为主、静动结合的分析方法，对高速铁路桥上无砟道岔的参数影响规律及典型设计难题进行了系统研究[120]，设计、开展了高速铁路桥上无砟道岔的现场综合试验，并对高速铁路桥上无砟道岔典型工点进行了系统检算评估。

北京交通大学赵磊[121]在其博士学位论文中从无砟轨道设计理念出发，通过设计及检算方法的创新，用细部参数现场试验等手段，提出了无砟轨道精细化分析模型，主要由无砟轨道空间设计模型、预应力配筋检算模型及精细化层间病害分析模型构成，并将其应用于无砟轨道设计、检算及病害分析过程中。

北京交通大学梁淑娟[122]在其硕士学位论文中以断板条件下长大桥梁上CRTSⅡ型板式无砟轨道为研究对象，分析了断板对轨道-桥梁系统受力特性的影响，并基于结构可靠度理论提出了一种病害条件下无砟轨道-桥梁系统可靠性评估方法。

蔡小培等[123]针对CRTSⅡ型板式无砟轨道，分析了轨道层间阻力大小及道床板伸缩刚度等因素对桥上无砟轨道无缝线路长钢轨纵向力与位移的影响，根据桥上无缝线路受力特点及其变形规律，基于光纤光栅测试技术，在渭河特大桥上布设了多个监测点并对其进行长期监测，通过监测数据和理论计算设计出了一套用于渭河特大桥上的伸缩调节器布设方案，且该方案能满足铺设无缝线路的需要和操作要求[124]。

北京交通大学王冠通[125]在其硕士学位论文中建立了桥上板式无砟轨道三维实体有限元模型，探讨了桥上CRTSⅠ型和CRTSⅡ型板式无砟轨道在地震动作用下的受力特性。

北京交通大学安彦坤[126]等对比分析了箱型梁在整体温差荷载和温度梯度荷载作用下的桥上无缝线路伸缩力，结果表明采用温度梯度荷载的计算结果偏小，但考虑到这种荷载更符合现场实际情况，故需对梁体的温度场进行深入的试验性研究[127]。

北京交通大学刘克旭[128]在其硕士学位论文中以CRTSⅠ型板式无砟轨道为例，分析了多种复杂温度荷载和轨道病害条件下的桥上无缝线路纵向力学行为。

为研究不同类型的单元式无砟轨道在大跨桥上的适应性，中国铁道科学研究院王继军等[129]以CRTSⅠ型和CRTSⅢ型板式无砟轨道为例，对温度荷载作用下轨道各层结构纵向受力与变形、层间错动位移、限位结构受力进行了对比分析，结果表明CRTSⅢ型板式无砟轨道更有利于控制无砟轨道-桥梁相对位移及大跨梁端限位结构受力。

华东交通大学张鹏飞、桂昊等分别根据CRTSⅠ型[130-132]、CRTSⅡ型[133-135]和CRTSⅢ型[136-138]板式无砟轨道在我国高速铁路多跨简支梁桥和大跨连续梁桥上的应用情况，充分考虑各轨道结构、桥梁结构的空间力学特性及纵横垂向的相互作用关系，建立了精细化的有限元模型，研究了温度荷载、列车荷载及列车制动荷载作用下桥上轨道结构的受力与变形特性，并分析了荷载、轨道、桥梁参数等对轨道结构受力与变形的影响规律，对桥上扣件纵向阻力、固定支座墩（台）顶纵向刚度及滑动层摩擦系数的取值提出了合理的建议。