国外桥上无缝线路纵向力计算理论以日本及欧洲的国际铁路联盟（International Union of Railways，简称UIC，UIC是法文全称的缩写）的研究最具代表性，两者均在高速铁路的建设中得到了极大的发展。

1. 日本

20世纪60年代初，日本在新干线上铺设了大量的无缝线路，提出了在计算桥上无缝线路伸缩力时采用梁轨相互作用法[51]，如图1-6所示；1979年，佐藤裕等在其专著《日本东海道新干线轨道研究》[52]中介绍了新干线的轨道设计方法，推导了桥上铺设长钢轨时梁轨相互作用力；2007年，日本铁道科技研究所的松本信行等[53]以本四联络线上的南（北）备赞-濑户大桥为例，介绍了桥上无缝线路的设计原则及扣件阻力控制等情况。

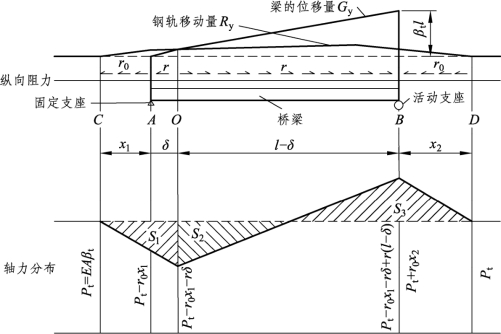
图1-6　日本桥上无缝线路伸缩力计算原理

2. 欧洲

（1）捷克的梁轨相互作用分析模型。

1974年，捷克学者Frÿba提出了“准静态分析理论”[54-57]，即假定钢轨和桥梁为抗弯刚度无穷大的等截面弹性轴力杆，将线路纵向阻力假定为线弹性变化，视制动力和牵引力为静力荷载，将集中力用数学形式表示为均布荷载，列出轴向平衡微分方程并采用拉普拉斯变换法求解微分方程组；但该方法并未考虑梁体弯曲、墩顶位移、桥梁下部结构刚度和纵向阻力非线性的影响。

（2）德国双线性阻力计算模型。

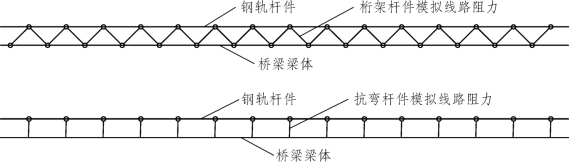
1964年，德国学者Siekmeier[58]采用试验的方法对线路纵向阻力-纵向位移关系进行了研究，但受加载设备能力的限制，线路的纵向位移不足1 mm。在此基础上，1980年，Seraphim[59]截取了10 m长的线路进行加载，使线路纵向滑移10 cm以上，测定了纵向滑移阻力规律，结果表明轨排中的道床在线路与路基相对位移超过4 mm后开始发生松动。Talker[60]于1978年对另一段线路的滑移试验也得出了类似的结果。德国学者提出的梁-轨联结模型假定钢轨与梁体的连接为纯拉压或纯抗弯杆件，钢轨与道床的连接可采用桁架或抗弯杆件两种方式，如图 1-7 所示。Moelter[61]分析了桥梁发生挠曲变形时梁体与桥台间以及相邻桥梁间上拔力的产生机理，介绍了梁体之间闭合装置与开放装置的适用条件。2006年至2009年间，德国累斯顿工业大学P.Ruge和C.Birk教授等[62-64]指出欧洲规范在计算纵向附加力时采用先单独计算后线性相加进行检算的方法存在不足，提出了考虑前期加载历程的桥上无缝线路纵向附加力计算方法，并对比了该方法与传统线性叠加法之间的差异。

(www.daowen.com)

图1-7　德国梁轨联结模型

（3）UIC标准中的计算模型。

20世纪60年代开始，UIC试验研究所针对列车制动/起动条件下无缝线路与下部桥梁结构的相互作用关系进行了研究，并在2001年对其进行了完善[65]，提出采用梁单元模拟桥梁和长钢轨，采用线性弹簧单元模拟墩台顶刚度，而线路纵向阻力则需要采用非线性弹簧来模拟，为减小边界条件的影响，并规定路基段钢轨计算长度至少取100 m，如图1-8所示。

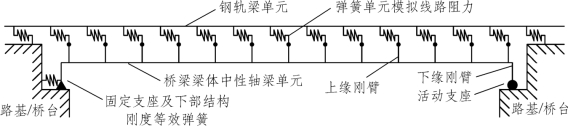
图1-8　UIC梁轨相互作用模型

（4）其他非线性阻力模型。

1964年，鲍列耶夫柯[66]推导了一种解析算法，用于计算桥上长钢轨纵向力，但该方法未考虑梁体弯曲的影响；1989年，荷兰代尔夫特理工大学的Coenraad Esveld[67]阐述了采用有限元法计算桥上无缝线路纵向力的思想，并对几种应用较为广泛的纵向阻力模型进行了总结；2003年，英国的Place和Davis等[68]在考虑线路纵向阻力非线性变化的基础上，分别采用线性反应谱法和非线性时程法分析了地震作用下桥上无缝线路纵向力特性。

3. 其他国家

1982年，印度学者A.S.Arya和S.R.Agrawal[69]提出了用于分析梁轨相互作用的传递矩阵法，该方法考虑了梁体竖向位移和墩顶纵向位移，但并未考虑轨道的竖向位移，且其解析能力有限，不适宜用于分析未知数较多的长大跨度桥梁；2009年，Rui Calcada[70]总结了国际上对于梁轨相互作用的多种方法和成果，P. Ramondenc等[71]详细阐述了梁轨相互作用机理，详细介绍了无缝线路纵向附加力的形成机理，提出“桥梁必须适应线路而非线路必须适应桥梁”的设计理念；2011年，Roman Okelo和Afisu Olabimtan[72]提出采用有限元法建立三维模型，可更好地完善对梁轨相互作用关系的空间描述；2013年，H. Sedarat等[73]建立了精细化的有限元模型，对比分析了支座布置对浮桥上梁轨相互作用的影响。