（一）地震的能量

地震是地球内部缓慢积累的能量突然释放而引起的地球表层的振动现象。火山爆发和地震都是地球内部能量释放到地表上来的一种能量过程。在地震发生后，要发生各种能量转换，特别是地壳中的应变能向地震波动的动能转换，这是一种重要的现象。地震最大为8.9级，一次于1906年发生在哥伦比亚与厄瓜多尔边境，一次于1923年发生在日本，另一次于1960年5月22日发生在智利。如果把最大地震所释放的能量换算成电能，约相当于一座100万kW的发电厂在25年里发出的总电量。

地表的升降是地基重力位能变化的表现，断层面的生成可认为是应变能变化的结果。要估算波动能以外的能量变化一般是困难的。这是因为，我们对于地球内部能量转换的情况还很不了解。发生海底大地震时，产生海啸动能。地震最直接的表征是地基的振动，这就是动能，它是从震源发出的一种波动。这种能量是根据地表或其附近的地面震动来计算的，但是由于地震波在传播路程中有衰减，所以计算是很麻烦的。

（二）地震的震级与烈度

地震学上用地震震级和地震烈度两个不同概念来衡量地震的大小。地震震级反映地震释放的能量大小，有时也叫地震强度，是用来说明某次地震本身大小的，只跟地震释放的能量多少有关。地震能量越大，震级就越大。震级标准，它是用“级”来表示，最先是由美国地震学家里克特提出来的，所以又称“里氏震级”。它是根据地震仪器记录推算得到的。地震越强，震级越大。震级每相差1级，能量相差约32倍；每相差2级，能量相差约1 000倍。也就是说，一个6级地震相当于32个5级地震，而1个7级地震则相当于1 000个5级地震。在地震学上震级常用于研究与地震活动性有关的问题，而人们通常关心的是某次地震对具体地点的实际影响程度，也就是所谓的地震烈度。在地震学里，“烈度”已被用作说明地震影响的专门名词。

1.地震震级或强度

震级是表征地震强弱的量度，通常用字母M表示。以地震过程中释放出来的总能量来衡量该地震本身的大小，是比较合理的途径。但是，很大一部分能量在地下深处震源地方消耗于地层的错动和摩擦，转化为位能和热能。人们所能观测到的主要是以弹性波形式传到地表的地震波能量。一般就是根据这部分能量来推算地震震级或强度的。地震按震级大小可分为：弱震，即M＜3级的地震，如果震源不是很浅，这种地震人们一般不易觉察；有感地震，即3≤M≤4.5级的地震，这种地震人们能够感觉到，但一般不会造成破坏；中强震，即4.5≤M≤6级的地震，属于可造成破坏的地震，但破坏轻重还与震源深度、震中距等多种因素有关；强震，即M≥6级的地震，其中M≥8级的地震称为巨大地震。地震学上把发震时刻、震级、震中统称为“地震三要素”。

破坏性地震是指造成人员伤亡和财产损失的地震灾害。一般M≥5级时，就会造成不同程度的地震灾害，通常称为破坏性地震。地震记录上振幅的大小，除与震级有关外，还受距离、传播介质、地震台址土质、震源深度和错动的方向性，以及地震仪的特性等因素的影响。从大量观测数据中，可以确定各地震台的土质和所用仪器等因素的影响，求得各台的校正值。重要地震的震级，常取不同距离、各个方位上的地震台测定震级的平均值，以消除由于传播介质和震源机制等原因引起的差异。在地震学中，通常使用以下三种震级标度：

（1）地方震级（ML）。它采用里克特测定美国南加州地震震级的原始定义，结合当地情况，修订起算函数。我国主要地震区多已根据统计资料制定了本地区的震级标度。

（2）面波震级（ME）。1945年，古登堡给出了以周期接近20 s的面波振幅的最大水平向量和为依据的面波震级公式。苏联和东欧地震学者于1966年提出了以振幅与周期之比代替振幅的公式。近年来国内外一些工作证明，用竖直向面波最大振幅与用水平向振幅最大向量和求得的震级值相近，因而简化了测定工作。

（3）体波定级（MB）。体波波型比较单纯，容易测量振幅。以前通用古登堡和里克特于1956年提出的以中周期地震仪所记最大体波振幅为依据的公式。高灵敏度短周期地震仪推广以后，国际地震中心的报告中改用P波前三个周期中的最大振幅计算体波震级，用MB表示。

全国性的地震台网通常用基本台的记录计算面波震级。地区性的台网从区域台的记录计算地方震震级，有时还换算成面波震级。从中等强度的浅源地震的体波震级和面波震级可以统计出它们之间的经验关系，并据以进行换算。由于体波震级随地震强度的增加而趋于“饱和”，大地震的体波震级一般偏低，不符合以地震波能量为基础测定地震大小的概念。因此，通常用面波震级来研究正常深度地层的活动性。但是，深源地震的面波不发育，其地震图与浅源地震很不相同。能量相同的深源地震的面波震级远较浅源地震的小，所以通常用体波震级来描述深震的强度。

2.地震烈度

同样大小的地震，造成的破坏不一定相同，同一次地震，在不同的地方造成的破坏也不一样。为了衡量地震的破坏程度，科学家又“制作”了另一把“尺子”——地震烈度，它是某一地震在具体地点所引起振动影响的强度，是地震在地面产生的实际影响，即地面运动的强度或地面破坏的程度。烈度不仅与地震本身的大小（震级）有关，也受震源地方岩层错动的方向、震源深度、离震中的距离、地震波所通过的介质条件、表土性质、地下水埋藏深度，以及建筑物的动力特性、建筑材料、设计标准、施工质量和维护情况等许多条件的综合影响。震源是地球内部直接发生破裂的地方。震源深度是震源到地面的垂直距离。震中距是在地面上从震中到任一点的距离。(www.daowen.com)

一般来讲，一次地震发生后，震中区的破坏最重，烈度最高，这个烈度称为震中烈度。从震中向四周扩展，地震烈度逐渐减小。所以，一次地震只有一个震级，但它所造成的破坏，在不同的地区是不同的。也就是说，一次地震，可以划分出好几个烈度不同的地区。例如，1976年唐山地震，震级为7.8级，震中烈度为11度；受唐山地震的影响，天津市地震烈度为8度，北京市烈度为6度，再远到石家庄、太原等只有4～5度。

由于在同一地震的作用下，各地烈度不同。研究地震影响，要按强弱分等级，首先需要有作为区分标准的地震烈度表，以地震烈度作为尺度进行研究。在地震仪器还没有发展以前，地震强弱的评定不得不以宏观现象为依据。起初工作比较粗糙，烈度标准含混，各烈度间多无明确界线，评比不易精确。随着研究的日益深入，工作渐趋细致。在大量资料的基础上，经分析比较，制订了比较明确的地震烈度表，称为宏观地震烈度表（表3-3），并且得到了广泛的应用。我国也把烈度也划分为12度，不同烈度的地震，其影响和破坏程度不同。

表3-3　宏观地震烈度

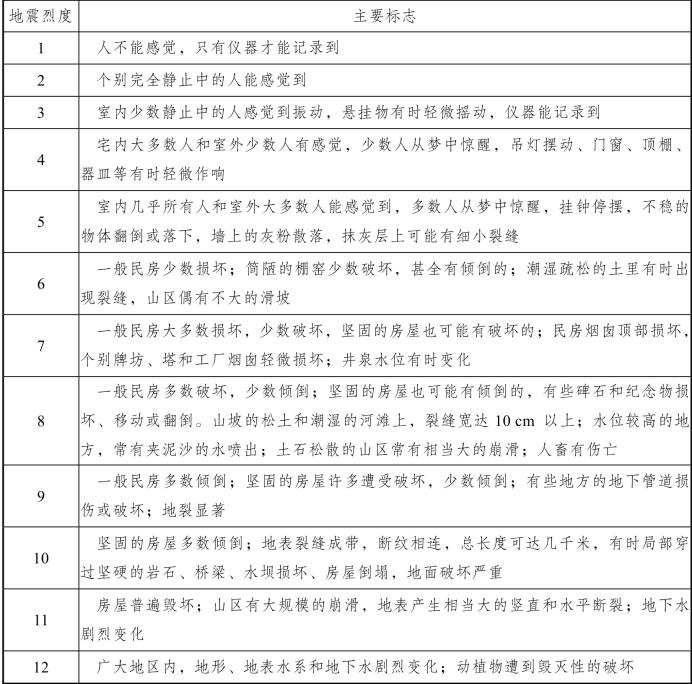
但是，为了进行工程抗震设计，从工程地震的观点来评定烈度，其主要目的是要确定抗震设计所需的地震作用力。如果不能找出一个与地震烈度相当的物理量来说明地震振动的强度，那么纵然能够正确地评定地震烈度，仍然难以运用到工程设计的实际计算中。因为工程设计人员不能仅仅根据上述宏观资料的一般性叙述，来确定对各类型建筑物和构筑物应采取什么样的抗震措施；他们需要一个能说明振动强度的定量数据作为计算依据，即定量地震烈度表。为了给实际计算抗震措施提供一个与地震烈度相当的物理量，长期以来人们在不断地探索解决这一问题的途径。最初，试图以引起物体振动或破坏的加速度作为与地震烈度相当的物理量，因为加速度可以从地震记录上直接推算。有了地面运动加速度值，工程设计人员即能计算作用于建筑物的地震力，从而确定怎样的抗震措施。通常认为，建筑物要承受重力作用，在竖直方向上有很大的稳定性，所以不必考虑竖直向的加速度而只需考虑水平向的最大加速度。应该注意的是，随着城市人口的密集，“垂直地震”出现的危害加剧，竖直向的加速度也不容忽视。20世纪上半叶，许多学者在地震烈度表这方面做过不少观测、实验和研究工作，并改进了以地表运动的最大水平加速度为衡量标准的“动力”或“绝对”地震烈度表。其中，1904年意大利地震学家坎坎尼提出的数值（表3-4），曾被许多国家用作抗震建筑的设计标准。

表3-4　“动力”或“绝对”地震烈度

这类烈度表的特点是以建筑物的破坏现象为评比烈度的主要依据，并以地表运动的最大水平加速度表示引起破坏的地震力。这种按照静力理论计算地震荷载的方法在处理抗震措施时非常简便。它是从观测和实践经验中得来的，所以有一定的实用价值，在一些国家中沿用甚久。

3.震级与烈度的关系

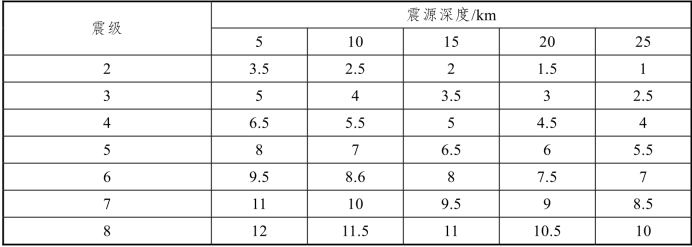
自从应用震级以来，各国地震工作者就在不断关注和研究震级和烈度之间的关系。在一定的地区范围内，在震源深度等条件相近的情况下，震级与烈度之间可以建立起一定的联系。比较肯定的结果是：当环境条件相同时，震级愈大，震源愈浅，震中距离愈近，地震烈度愈高。许多学者根据所掌握的具体资料，分别提出了相应的经验公式。有学者通过对比各主要公式，并以多次国内地震的实际情况予以验证，初步得出了“震中烈度”随震级和震源深度变化的粗略关系表（表3-5），表中烈度系以干燥的中等坚实土（如粉质黏土）为准。

表3-5　震中烈度与面波震级和震源深度关系