岩石（岩体）的断裂（破裂）也称破坏，断裂（破裂）的准则又称强度理论。

（一）脆性断裂

岩石（体）断裂（破裂）前很少有永久变形，即使有永久变形，总应变也不超过1%～3%，岩石断裂属于突变。岩石的强度（可以是压应力、拉应力或者剪应力等）超过某一极限值就发生破坏，适用的理论如最大正应力理论（σ拉＜[σt]）、最大剪应力理论和应变能理论等。

（二）莫尔强度理论——剪切破裂

莫尔强度理论是建立在试验数据统计分析的基础之上的。1910年，莫尔提出材料的剪切破坏。在复杂应力状态下，某一斜面上的剪应力达到极限值时，材料沿该斜面发生剪切滑移破坏，破坏面上的剪应力是该斜面上的法向应力σ的函数，可表示为τf=f（σ）。莫尔强度包络线是指各极限状态下应力圆上破坏点所组成的轨迹线。由于岩性条件不同，莫尔强度包络线、莫尔圆圆心的位置、莫尔圆半径的大小决定了抗剪强度的大小。实际破裂面分为两组，一组和最大主应力作用面成45°+φ/2的夹角，另一组和最大主应力作用面成135°-φ/2的夹角。

莫尔强度理论用两向应力状态来表示三向应力状态，未考虑中值主应力的影响，由此带来了一定的误差，约15%左右。

在三向应力状态下，三向抗压强度可以写为σc3=σc1+qσ3。当σ3=0时，得到单向抗压强度σc1=2c[（tan2φ+1）1/2+tanφ]，其中q为三向抗压强度的提高系数，q=[（1+tan2φ）1/2+tanφ]2，其中c、φ分别为岩（土）材料的内聚力和内摩擦角。

强度线是由一系列极限状态下的莫尔圆拟合得到的包络线，可以是直线、抛物线及双曲线等形式，由试验拟合得到，如图2-7所示。

图2-7　莫尔-库仑强度包络线

（三）岩石断裂力学理论基础——格里菲斯理论

1920年，格里菲斯（Griffith）基于脆性断裂理论，认为在脆性材料内部存在着许多杂乱无章的扁平微小张开裂纹。在外力作用下，这些裂纹尖端附近产生很大的拉应力，导致新裂纹产生，原有裂纹扩展、贯通，从而使材料产生破坏。按照孔附近应力集中和能量平衡概念，得出了裂纹扩张的规律及解析式。这是线弹性断裂力学的理论基础。

岩体中裂纹将沿着与最大拉应力作用方向相垂直的方向扩展（图2-8），即：

式中：γ——新裂纹长轴与原裂纹长轴的夹角（°）；

　　　β——原裂纹长轴与最大主应力的夹角（°）。

图2-8　裂纹发展方向

根据扁平孔应力状态的解析解，得出格里菲斯强度（图2-9）判据：

（1）当σ1+3σ3＞0，破裂条件为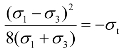：，最可能裂纹方位角：cos2β=

图2-9　格里菲斯强度曲线

（2）当σ1+3σ3≤0，破裂条件为：σ3=σt，最可能裂纹方位角：sin2β=0。(www.daowen.com)

如果应力点（σ1，σ3）落在强度曲线上或者曲线左边，岩石发生破坏，否则不破坏。

断裂力学已不把岩石看成连续的均质体，而看作由裂隙构造组合而成的介质。断裂力学分为线性断裂力学、弹塑性断裂力学；按研究裂纹的尺度可分为微观断裂力学和宏观断裂力学。运用断裂力学分析岩石的断裂强度可以比较实际地评价岩石的开裂和失稳，可用以分析工程中裂纹的出现以及预测岩石结构的破裂和扩展。

1962年，麦克·克林脱克等人认为，当应力σy达到某一临界值时，裂纹便闭合（图2-10），在裂纹表面产生法向应力和摩擦力，影响新裂纹的发生和发展。这种摩擦力是格里菲斯断裂理论中没有考虑到的。因此，对格里菲斯理论进行修正，得到：

式中：f——为裂纹面之间的摩擦系数。

图2-10　裂纹闭合后的情况

（四）Hoek-Brown经验准则

霍克（Hoek）和布朗（Brown）发现，大多数岩石材料（完整的岩块）在三轴压缩试验破坏时的主应力之间可用式（2-7）来描述。

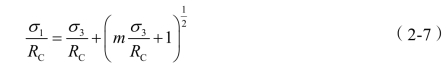
式中：m——与岩石的类型有关，取值范围7～25，如节理发育的灰岩可取7，节理不发育的砂岩可取15，花岗岩可取25；

　　　RC——岩石单轴抗压强度（MPa）。

以上为岩石（岩块）的破坏准则，对于岩体，霍克和布朗建议如下的经验破坏准则：

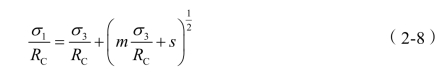
式中：s——为常数，取值范围0～1。反映了在承受破坏应力σ1和σ3之前，岩石扰动或损伤的程度。s=1，为完整岩体，s=0，为完全破碎的岩体。

岩体单轴抗压强度：

岩体单轴抗拉强度：

岩体剪应力表达式：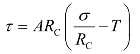

Hoek-Brown强度准则如图2-11所示。

图2-11　Hoek-Brown强度准则