（一）岩石在单向荷载作用下的变形

在中、低压力作用下，应力-应变关系可分为三类，如图2-2所示。

（1）弹性、似弹性，应力-应变曲线呈直线型，弹性模量E≥（6～11）×104 MPa。

（2）半弹性，应力-应变曲线稍显弯曲，有的岩石凸向斜上方，有的岩石凸向斜下方，弹性模量E=（4～7）×104 MPa。

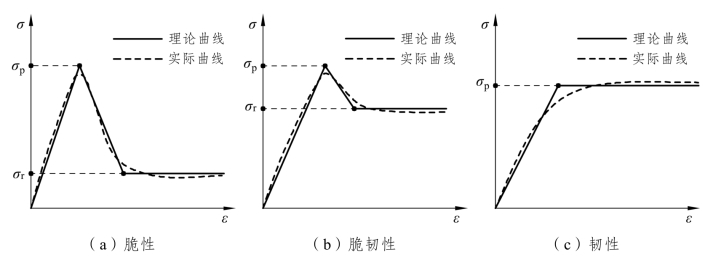
图2-2　不同类型岩石的应力-应变关系

（3）无弹性或弹塑性应力-应变呈曲线，凸向斜上方，弹性模量E＜5.0×104 MPa。

除典型的线性弹性岩石之外的多种岩石，特别是微裂隙发育的岩石，在加荷的初始段，应力-应变关系均呈曲线，因为这是微裂隙的压密阶段，所以不呈直线。工程上不使用这一段曲线。

上述的弹性、似弹性类岩石，在卸荷时的表现又分两种情况，一类是卸荷时沿加荷时的直线回到原点，这是典型的线性弹性；另一类是卸荷后应变不直接回到原点，再经过一段时间，应变还会回到原点，这叫非线性弹性，最后的一段时间叫弹性后效（滞后）。

在高应力时，可能出现脆性破坏，也可能出现屈服，还可能出现加工硬化（应力-应变曲线的斜率增大）或软化（应力-应变曲线的斜率降低）。

（二）岩石在三向荷载作用下的变形

三向荷载和单向荷载相比，就是有了围压。围压很小时，基本上同单向应力状态，呈脆性破坏。随着围压增大，越来越表现出塑性，即破坏前的变形明显增大，甚至表现出黏性。致密砂岩在不同围压下的三轴应力-应变关系如图2-3所示。

三向应力作用不只和围压大小有关，还和最大最小主应力的差值σ1-σ3的有关。根据莫尔强度理论τmax=（σ1-σ3）/2，剪应力大时，会产生剪切破坏，岩体中经常存在两组交叉节理称X形节理，即剪切破坏的结果，两组节理中一组和水平面成45°+φ/2夹角，另一组节理成135°-φ/2夹角。

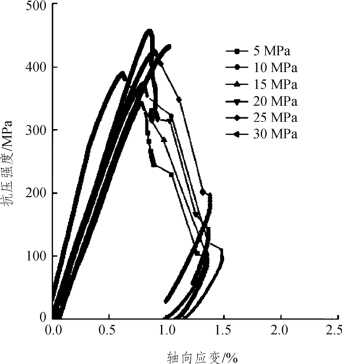
图2-3　致密砂岩在不同围压下的三轴应力-应变关系

（三）岩石在反复加荷和卸荷条件下的变形

在反复加载、卸载条件下，如果卸载点在弹性极限以内，则应变沿加载曲线回到原点；如果卸载点超过了弹性极限，则会出现弹性后效现象，甚至会出现塑性变形。

卸载曲线和加载曲线不重合，两者所夹的面积称塑性滞回环。在不断加载的情况下，继续加载曲线仍沿着单向连续加载曲线上升，只是加载曲线斜率有所减小，塑性滞回环面积有所增加。

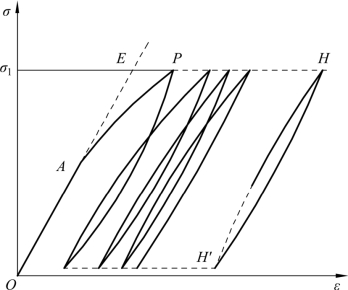
在同一级荷载作用下，卸载曲线和加载曲线的斜率大致平行。在同一级荷载下反复加载卸载，塑性滞环不断缩小，经过多次加载卸载后，卸载曲线和加载曲线几乎重合，这一点对岩石、岩体试验很重要，在同一级荷载作用下，经过多次加荷卸荷，弹性、弹塑性参数就趋于稳定了，甚至趋于常数。岩石的循环加载曲线如图2-4所示。

(www.daowen.com)

图2-4　岩石循环加载曲线

（四）岩石（体）的流变特性

材料的流变（蠕变、徐变）和两方面的因素有关，一是应力水平，应力（剪应力）不大于某个界限时，不发生流变；二是时间因素。从本质上说，弹性变形、塑性变形、流变变形都需要时间因素。在弹性变形中因时间极短而忽略不计，在塑性变形中，时间也不出现在方程中，只有在流变方程中，时间作为一个参数，明显出现在方程中。岩石蠕变试验曲线如图2-5所示。

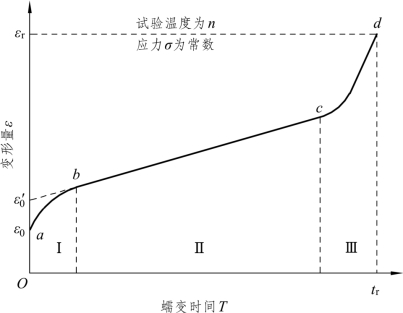
图2-5　岩石蠕变试验曲线

岩石的流变可表示为

式中：n——试验温度（°C）；

　　　E——变形模量（MPa）；

　　　G——剪切模量（MPa）；

　　　A——试验常数；

　　　t——流变时间（s）；

　　　σ——试验应力（kPa）；

　　　σ1——轴向应力（kPa）；

　　　σ2——围压（kPa）。

岩石与岩体应力-应变曲线的区别如图2-6所示。

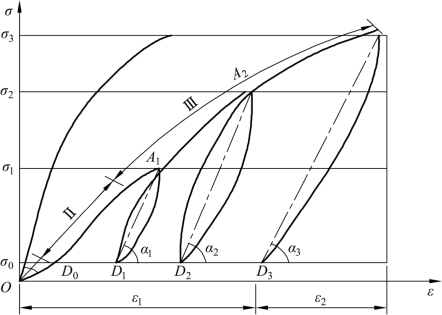
图2-6　岩石与岩体应力-应变曲线的区别