数字地面模型的概念是在1958年由美国麻省理工学院的Miller教授提出的，当时研究的目的是如何应用从摄影测量获得的数据通过数字化计算的方法来加快公路的设计，并成功地运用到公路的勘测设计中。数字地面模型（DigitalTerrainModel，DTM）是一个表示地形特征、空间分布的、有规则的数字阵列，也就是将地形表面用密集的三维坐标表示的一种数学表达形式。

数字地面模型不同于地形图、地形立体模型等直观表示地形的方法，而是以抽象的数字整列表示地貌起伏、地形形态的。虽然数模是一种不直观的、抽象的地形形态表示，人眼不能直观察觉，但这种地表形态对计算机的处理十分有利，计算机可以从中直接、快速准确地识别，进行数据处理，提供出方便的地形数据，以实现各种作业的自动化。

由于数模原始数据点的分布形式不同，数据采集方式的不同，以及数据处理、内插的方法不同和最后输出的方式不同等原因，数字地面模型的种类较多。根据数模中已知点的分布形式并考虑到数据输出格式及数据处理方式，可将数字地面模型大致分为规则数模、半规则数模、不规则数模三大类。

1.规则数模

规则数模是指原始地形点之间均有固定的联系，如方格网数模、矩形数模和正三角形格网数模。在格网之间的高程，常采用局部多项式进行内插。

由于每个已知点相对周围已知点的位置是固定的，所以按规则格网方式采集数据建立数模，量测地形点简单、客观、不需要判断地形，易于实现数据采集的自动化、半自动化。由于格网是规则等距的，在计算机中只需储存各个格网点的高程值，而平面坐标只需记录第一个网节点即可，其余节点的平面坐标根据其格网管理信息很容易在计算机中确定和恢复，这可节省计算机内存。这种只记录节点高程的数模，也称为数字高程模型（DigitalElevation Model或DigitalHeightModel，简称DEM或DHM）。该模型优点是输出形式简单、数据结构良好、便于应用，内插待定点高程时，检索与内插简单快速。该数模最大缺点是原始数据不能适应地形的变化，除十分均匀的地形外，已知点没有与地形特征点联系起来，易遗漏地形变化点；同时，由于数据采集按规则方格网的方式进行，一旦间距给定，所有已知点平面位置就是固定的，从而导致地面信息不足，而均匀平缓地区冗余数据点太多且精度不一现象，不能兼顾地形变化线和地形特征点，格网中也就难于测定地面坡度的变化，从而导致高程内插精度降低。若要使格网数模更好的表示地形，则只有将格网间距缩小，这将导致原始数据的采集工作成倍增加。格网数模一般适用于地形较平缓和变化均匀的区域，以及用于搜索地形等高线、绘制全景透视图和内插精度要求极高的路线平面优化中内插地面线等方面。

2.半规则数模

半规则数模是指各原始数据点之间有一定的联系，如用地形断面或等高线串表示的数模。

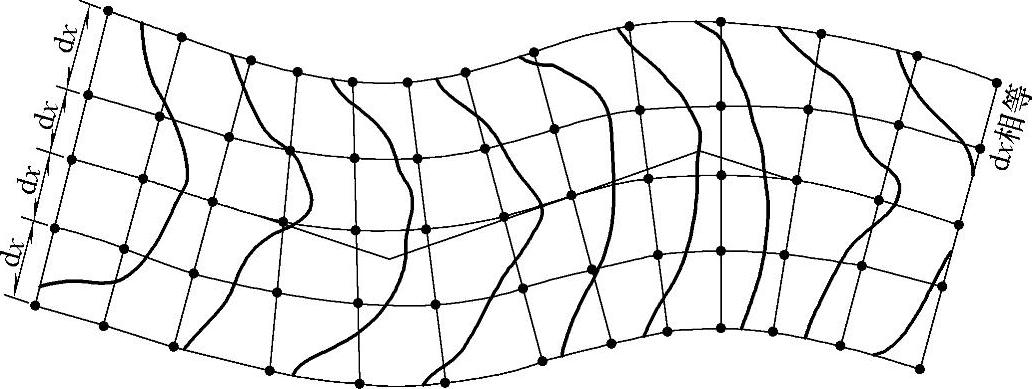
当以断面线高程表示地形时，任一串原始地形点表示某一特定地形剖面。各断面之间的距离及断面上点与点之间的距离可以固定的，也可以随地形变化而定。这种数模相当于用一批密集的、相互联系的地形剖面叠合在一起模拟地形，待定点的高程由相邻断面的高程点内插而来，如鱼骨式地面模型（见图11-1）。这是在路线方案确定以后沿道路纵、横断面采集数据，用一批相互联系的横断面地形剖面叠合在一起而形成数字地面模型。

(www.daowen.com)

图11-1 鱼骨式数字地面模型

沿等高线采集的一系列同一高程的x、y坐标的地形高程信息（二维线串），以及沿地形特征线、断裂线、地物、水系等各种信息采集的x、y、z三维坐标信息（三维线串）所组成的数模，称为串状数模。由于等高线具有在地形坡度大的地方密，在地形平缓处稀的特征，故地形点的分布与密度很好地适应地形的变化。此外，由于各种断裂线、地物和水系信息可用三维串线在数模中表示，为方便进行处理，使程序绘图能力大为加强，这是串状数模最突出的优点。半规则数模能较好地适应地形的变化，内插精度较高，但采集信息不能实现自动化，原始数据的分布和密度易受人的主观影响，建立数模过程中所需程序复杂。

3.不规则数模

不规则数模其原始地形数据点之间无任何联系，点的分布是随机的，一般常采集地形特征点、变坡点、山脊线、山谷线等处，常见的有散点数模、三角网数模等。

散点数模是将原始地形点看做一些随机分布的“离散点”，可认为点与点之间无任何联系。在这种已知点中直接进行内插其精度是不可靠的，因为不能确定由哪些点构成实际的地面。所以内插时先利用已知点拟合成一个局部的或区域的内插表面，然后再由该内插表面确定特定点的高程，这是这一类数模的特点。这种高程内插也称为移动曲面拟合法，在坡度变化大，地形起伏急剧改变的区域，特别是地物地形断裂线附近，这种曲面拟合则明显地很难描述出局部形状，而造成内插点的高差误差偏大。所以为提高内插精度，使之满足工程设计需要，除原始点的分布必须符合地形变化，保持足够的密度外，程序中必须具备对地物、地形断裂线处理的功能。

从数模的精度和计算速度两个方面来考察，散点数模不失为一种简单而有效的方法，具有很大的实用价值，在国内很多程序中得到应用。

三角网数模的基础是假设地表面可用有限个平面来表示。为此将地形已知点作为不重叠地覆盖在拟建数模区域之上的三角形的各顶点，将地表面看成是由这样小三角形平面所组成的折面覆盖起来的，用许多平面三角形逼近地形表面。当已知点较密及分布适当时可以很精确地表示地表面特征，而待定点的高程由该点所处的三角形平面来确定。在建立三角形数模的自动联网过程中，若将各地物线、地形断裂线和水系边缘轮廓线作为三角形边缘进行联网，能在程序中直接方便地处理地物、断裂线等问题。此外，由于三角网数模可以用地形特征点、特征线所组成的三角形平面来确定地形，在采样点的分布和密度符合地形变化，三角形联网合理时数模内插精度很高，达到同等高程内插精度时，该类数模所需要的原始地形点数量远少于其他类型数模所需的已知点数，这是三角构网的显著优点。三角网数模的缺点是采集原始地形数据完全依靠人的经验来选取地形点，易产生遗漏和复测现象，此外三角网的网形完全取决于原始地形点的分布，使数模的精度易受人为的影响，对采集地形数据要求较高。尽管如此，由于三角网数模能以较少的已知点去逼近地形，可以方便地处理地物、断裂线等，内插结果合理、精度高，仍不失为一种较好的数模建立方法。

不规则数模的特点：数据采集是随机的，一般是取地形特征点，所以较好地适应地形变化，内插精度较高。其缺点是需要人工判读地形，从而增加了数据采集的难度，此外构造数模较复杂、计算时间长。由于数模的优点较为明显，在实际工程设计中应用最为广泛。下面将对三角网数字地面模型作比较详细的介绍，具体算法读者可参考专门书籍。