1.直线型定线法

直线型定线方法是根据控制点或导向线和相应的技术指标，试穿出一系列与地形相适应的直线作为基本线形单元，然后在两直线转折处用曲线予以连接的定线方法，即传统的以直线为主的穿线交点定线法。平面线形以直为主，适用于地形简单的平原微丘区。

（1）路线标定 道路中线确定以后，必须采集交点坐标，并由此计算转角α和交点间距D；确定圆曲线半径R和缓和曲线长度L，计算平曲线要素和推算主点桩号；最后计算逐桩坐标。通常交点坐标的采集方法有直接采集法和定前后直线间接推算法两种。

1）直接采集法是在绘有格网的地形图上读取各交点的坐标，一般只能估读到米，适用于交点前后直线方向和位置限制不严的情况。

2）定前后直线间接推算法是在绘有格网地形图上先固定交点前后的直线（即在直线上读取两个点的坐标），再用相邻直线相交的解析法计算交点坐标，一般适用于交点前后直线方向和位置限制较严的情况。

当已知交点前直线上两点的坐标（X₁，Y₁）和（X₂，Y₂），后直线上两点（X₃，Y₃）和（X₄，Y₄），则交点坐标（X，Y）可由下式计算

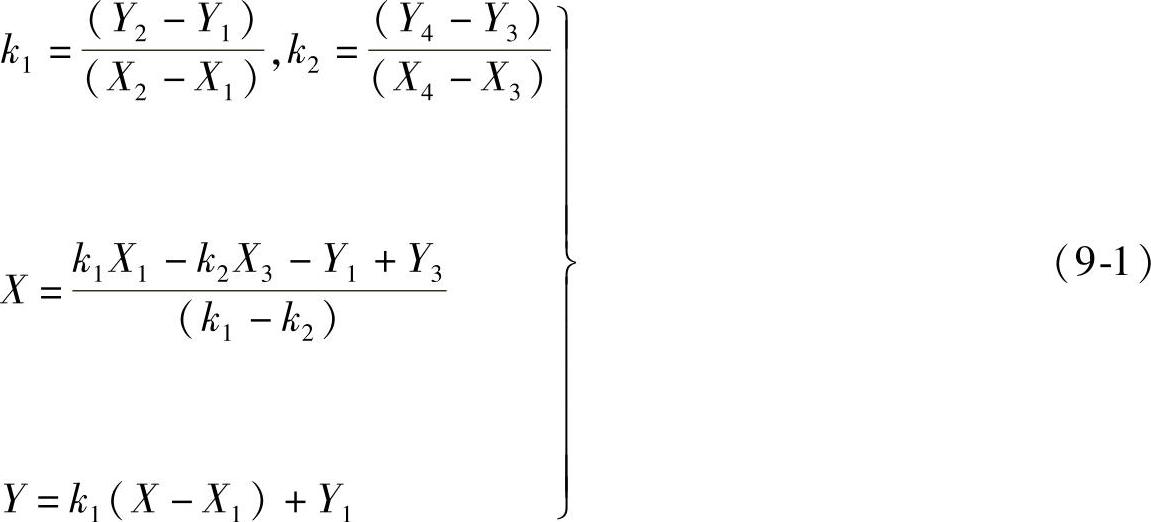
当X₁=X₂时 X=X₁=X₂，Y=k₂（X－X₃）＋Y3

当X₃=X₄时 X=X₃=X₄，Y=k₁（X－X₁）＋Y₁

（2）坐标计算 经纸上定线确定了交点坐标后，应先计算出路线转角、交点间距、平

曲线要素以及主点桩桩号，根据路线地理位置和几何关系计算出道路中线上各桩点的坐标，

编制逐桩坐标表，然后根据逐桩坐标实地放线。

1）路线转角、交点间距、曲线要素及主点桩计算。设起点坐标JD₀（XJ₀，YJ₀），第i个交点坐标为JD_i（XJ_i，YJ_i），i=1、2、…、n，则坐标增量

dX=XJ_i－XJ_i－1，dY=YJ_i－YJ_i－1（9-2）

交点间距

象限角

计算方位角A

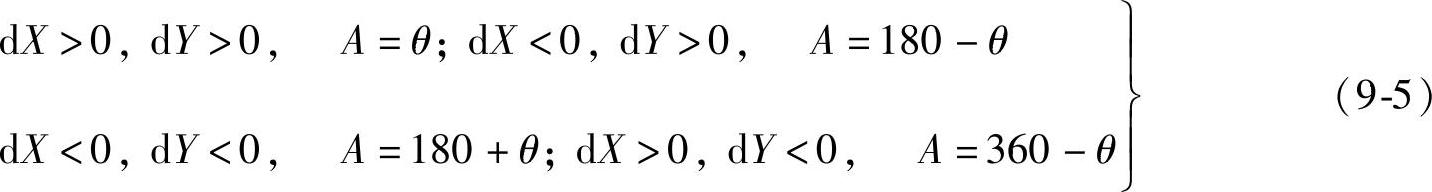
转角

一般情况下，αi为“＋”，曲线为右偏；αi为“－”，曲线为左偏。曲线要素及主点桩号计算公式与传统方法相同。对于高速公路，由于精度要求较高，计算时应注意取舍误差，否则会影响计算精度。

2）直线上中桩坐标计算。如图9-1所示，设交点坐标为JD（XJ，YJ），交点相邻直线的方位角分别为A₁和A₂，则ZH（或ZY）点坐标

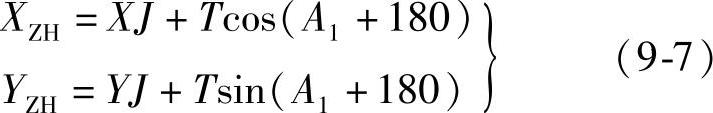
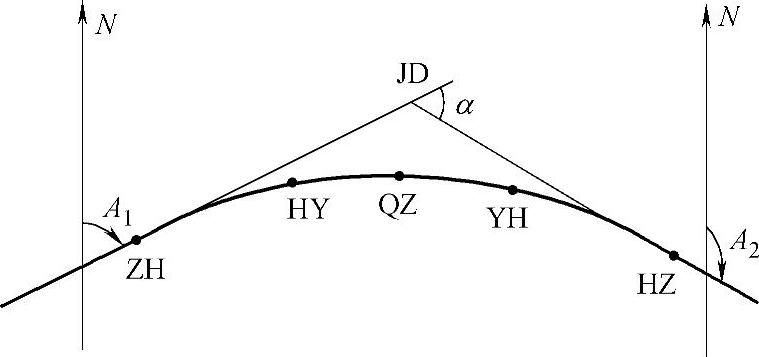
图9-1 中桩坐标计算示意图

HZ（或YZ）点坐标

设直线上任意桩里程为L，ZH、HZ表示曲线起、终点里程，则前直线上任意点坐标（L≤ZH）为

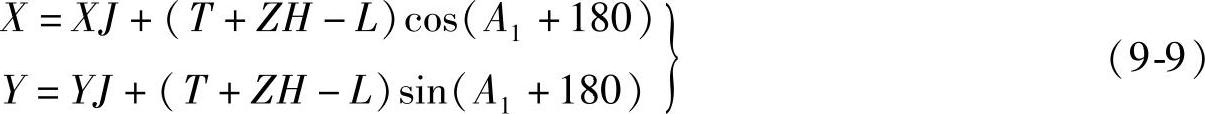
后直线上任意点坐标（L＞HZ）为

3）单曲线内中桩坐标计算

①不设缓和曲线的单曲线。设曲线起终点坐标分别ZY（X_zy，Y_zy），YZ（X_yz，Y_yz），则圆曲线上坐标为

式中 l——圆曲线内任意点至ZY点的曲线长；

R——圆曲线半径；

ξ——转角符号，右转为“＋”，左转为“－”，下同。

②设缓和曲线的单曲线。缓和曲线上任意点的切线横距

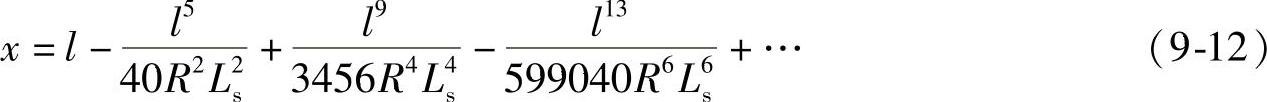
式中 l——缓和曲线上任意点至ZH（或HZ）点的曲线长；

L_s——缓和曲线长度。

a.第一缓和曲线（ZH～HY）内任意点坐标计算

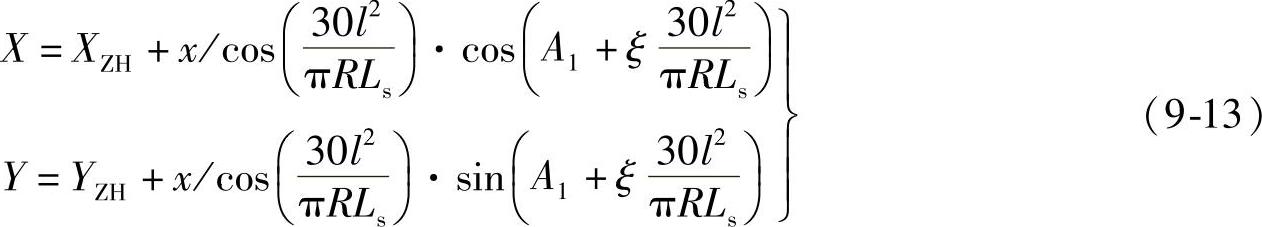
b.圆曲线内任意点坐标

由HY～YH时

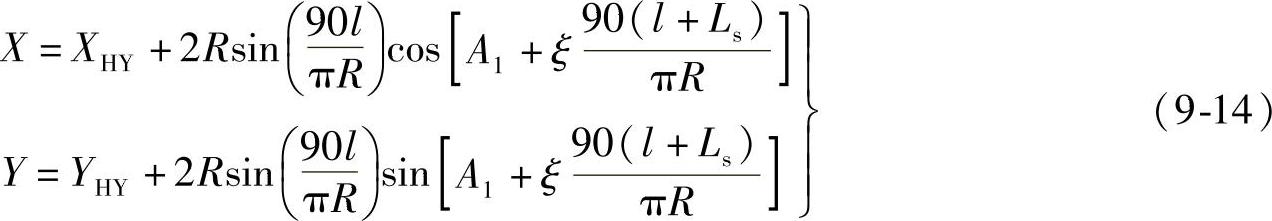
式中 l——圆曲线内任意点至HY点的曲线长；X_HY、YHY——HY点的坐标，由式（9-13）计算。

由YH～HY时

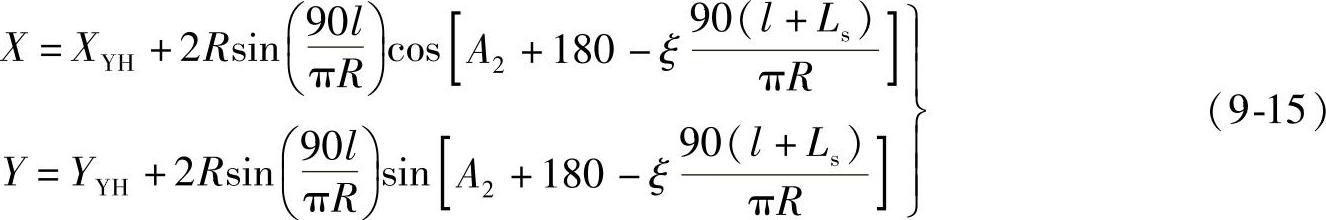
式中 l——圆曲线内任意点至YH点的曲线长。c.第二缓和曲线（HZ～YH）内任意点坐标

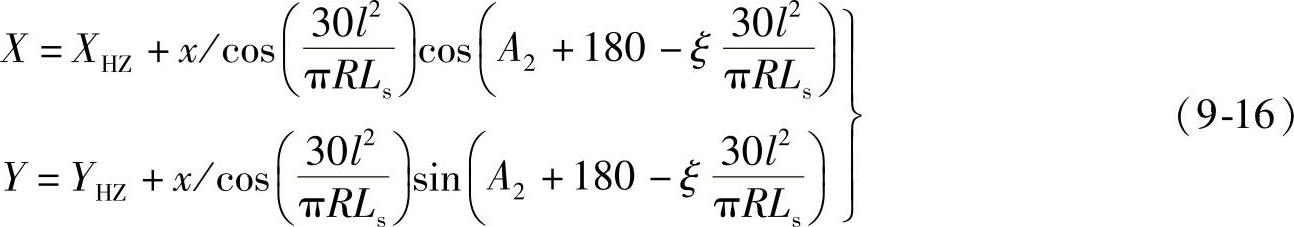
式中 l——第二缓和曲线内任意点至HZ点的曲线长。

4）复曲线坐标计算。

①复曲线中间缓和曲线L_F上任意点坐标。复曲线中间有设缓和曲线和不设缓和曲线两种情况，设缓和曲线时即构成卵形曲线。该缓和曲线仍然采用回旋线，但它曲率不是从零开始，而是截取曲率1/R₁～1/R₂这一段作为缓和曲线。如图9-2所示，缓和曲线AB的长度为L_F，A、B点的曲率半径分别为R₁、R₂，M为缓和曲线AB上曲率为零的点，AB段内任意点的坐标从M点推算。

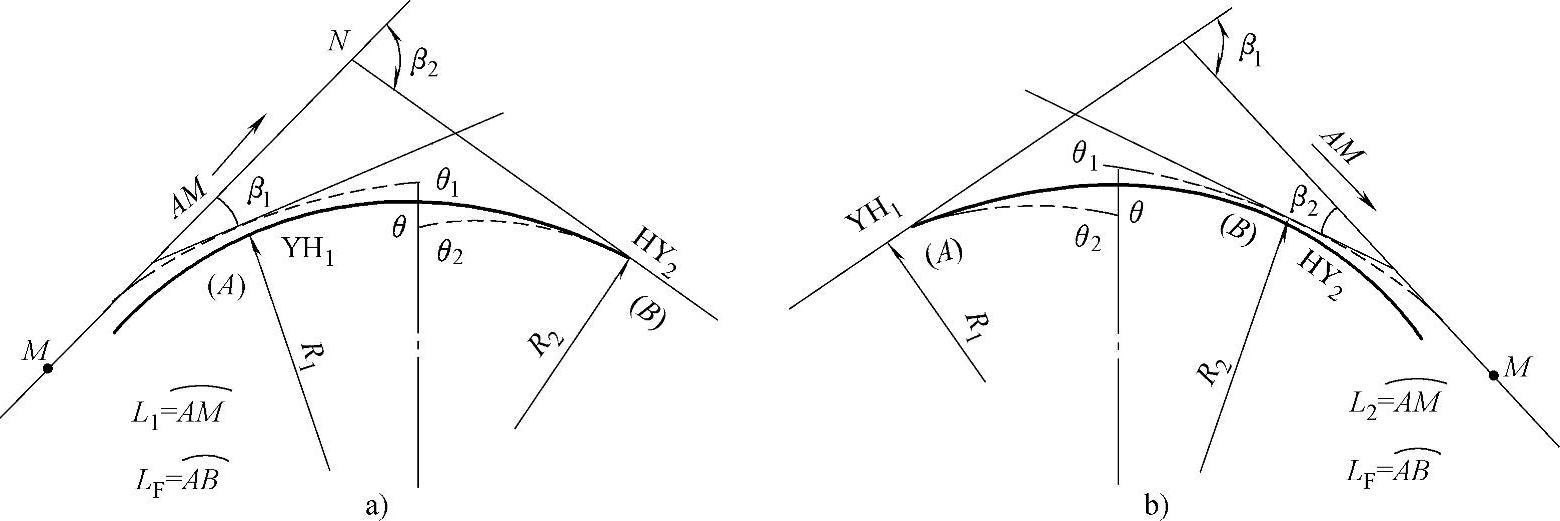
图9-2 复曲线坐标计算示意图

a）R₁＞R₂ b）R₁＜R2

根据回旋线几何关系

因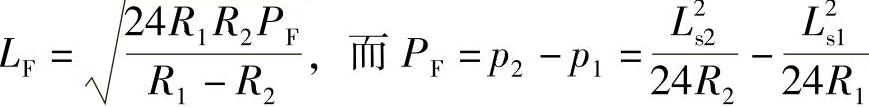，故

式中 L_s1、L_s2——第一、第二缓和曲线长度；

R₁、R2——L_F两端的圆曲线半径。

a.当R₁＞R₂时，如图9-2a所示，设A点（YH₁）的坐标为（X_A，Y_A），由式（9-14）计算得到，切线方位角A_A用下式计算

式中 l——半径为R₁的平曲线HY₁至YH₁的曲线长。

M点的坐标（X_M，Y_M）为

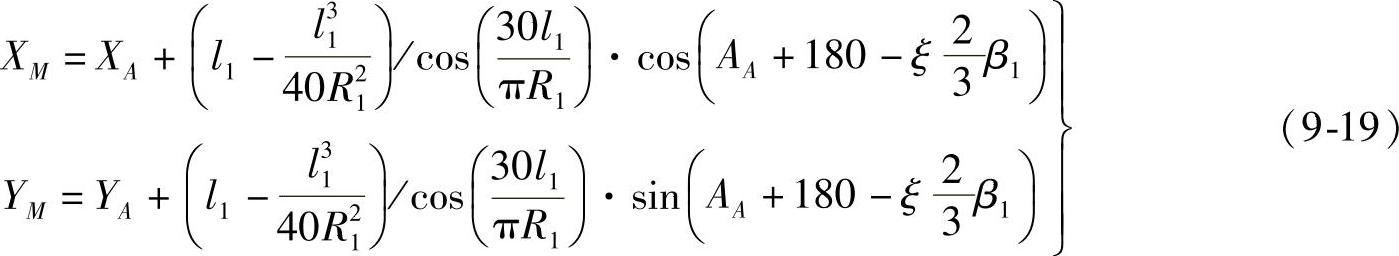
式中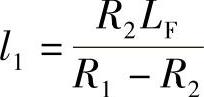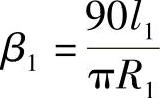，；；M点的切线方位角A_M=A_A－ξβ₁。

b.当R₁＜R₂时，如图9-2b所示，M点的坐标为

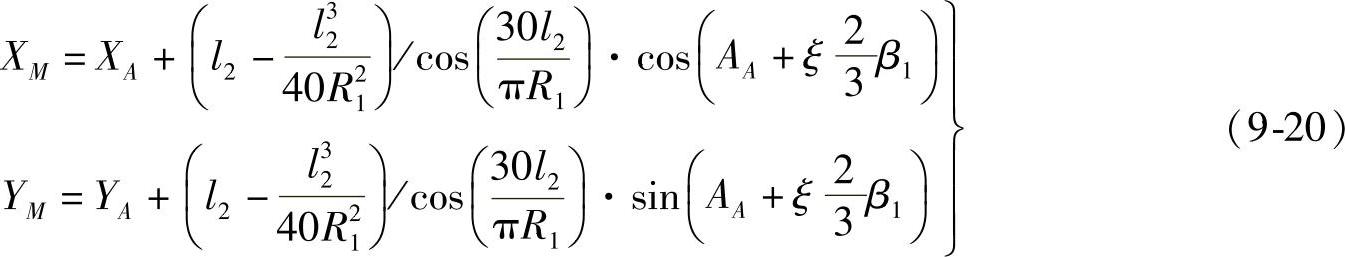
式中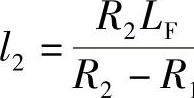，1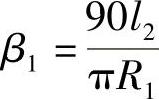；；M点的切线方位角A_M=A_A＋ξβ₁。

c.计算出M点的坐标及切线方位角后，当R₁＞R₂时，用式（9-13）计算L_F上任意点坐标；R₁＜R₂时，用式（7-11）计算L_F内任意点坐标。应注意的是，式中的l应为中间缓和曲线上计算点至M点的曲线长，A₁、A₂相应换成A_M。

②复曲线内L_F段以外的任意点坐标。复曲线内除L_F段外其他部位上任意点坐标计算公式同式（9-12）～式（9-16）。

2.曲线型定线法

根据导向线和地形条件及相应技术指标，先用一系列圆弧去拟合控制较严的地段或部位，然后把这些圆弧用适当的直线或缓和曲线连接起来，形成以曲线为主的连续线形。平面线形以曲线为主，适用于地形、地物复杂的山区和丘陵区，以及地物障碍较多的平坦地区。

（1）定线步骤

1）参照导向线或控制点，画出线形顺适、平缓并与地形相适应的概略线位。

2）用直尺或不同半径的圆曲线弯尺拟合概略线位，形成一条由圆弧和直线组成的具有错位（即设缓和曲线后圆曲线的内移值）的间断线形。

3）在圆弧和直线上各采集两点坐标或在计算机上拾取圆弧和直线对象固定位置，通过试定或试算，用合适的缓和曲线将它们顺滑连接，形成连续的平面线形。

（2）确定回旋线参数确定回旋线参数A值是采用曲线型定线法的关键。过去多采用回旋曲线尺或表法，即用不同整数的回旋线参数A值制作回旋线长度与曲率半径具有对应关系的尺或表，供使用时查对。随着计算机的广泛应用，目前主要采用解析法确定A值。解析法是根据几何关系，建立含有参数A的方程式，通过计算精确求解A值。下面分三种情况介绍。

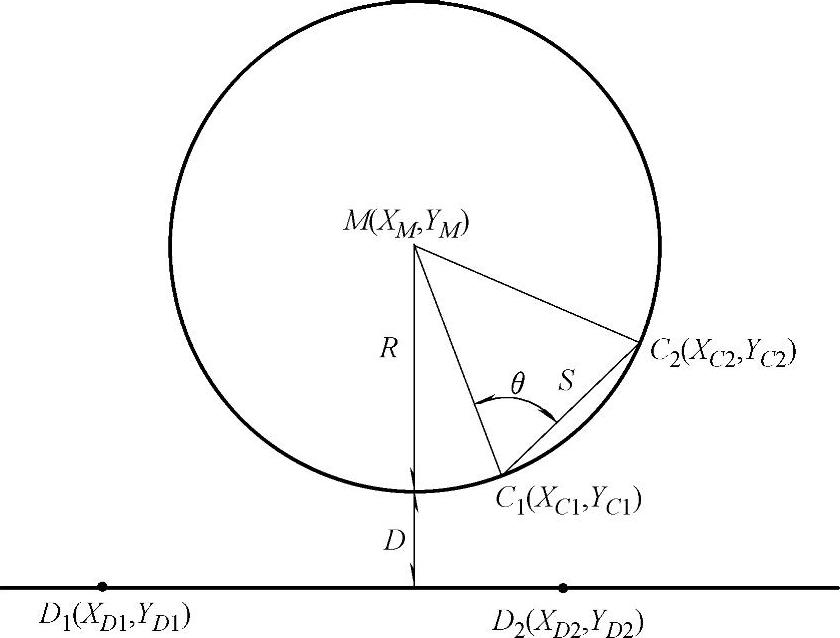
图9-3 直线与圆曲线连接计算图

1）直线与圆曲线连接。如图9-3所示，已知直线上两点D₁（X_D1，Y_D1）、和D₂（X_D2，Y_D2）和圆上两点C₁（X_C1，Y_C1）、C₂（X_C2，Y_C2）以及圆曲线半径R。

①求圆心坐标。由图9-3得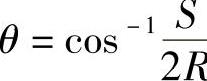R，

C₁M方位角α_C1M=α_C1C2＋ξθ，其中α_C1C2为

C₁C₂的方位角。圆心坐标为

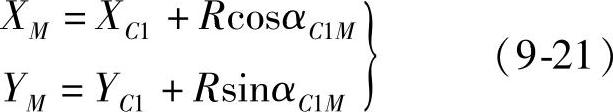
式（9-21）中R=R，下同。

②直线与圆曲线间距D令

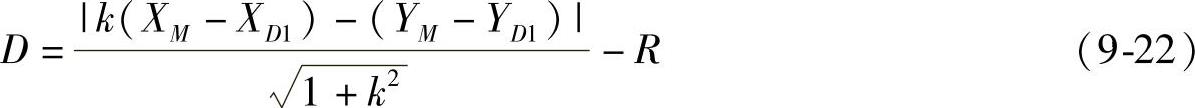
式中，。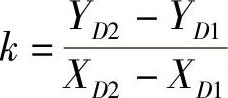

③回旋线参数A及长度L_s。由回旋线的几何关系，其内移值为

p=y＋Rcosτ－R（9-23）

式中，；。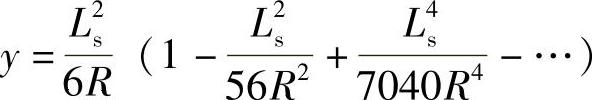

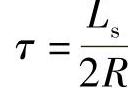因p=D，故式（9-23）只含未知数L_s，可采用牛顿求根法解出L_s，一般精确到10^－4。则参数A值计算公式为

2）两反向曲线连接。如图9-4所示，已知两圆曲线上两点坐标及相应半径R₁和R₂，用上述计算方法求出两圆心坐标M₁（X_M1，Y_M1）和M₂（X_M2，Y_M2）后，按下述步骤计算参数A值。

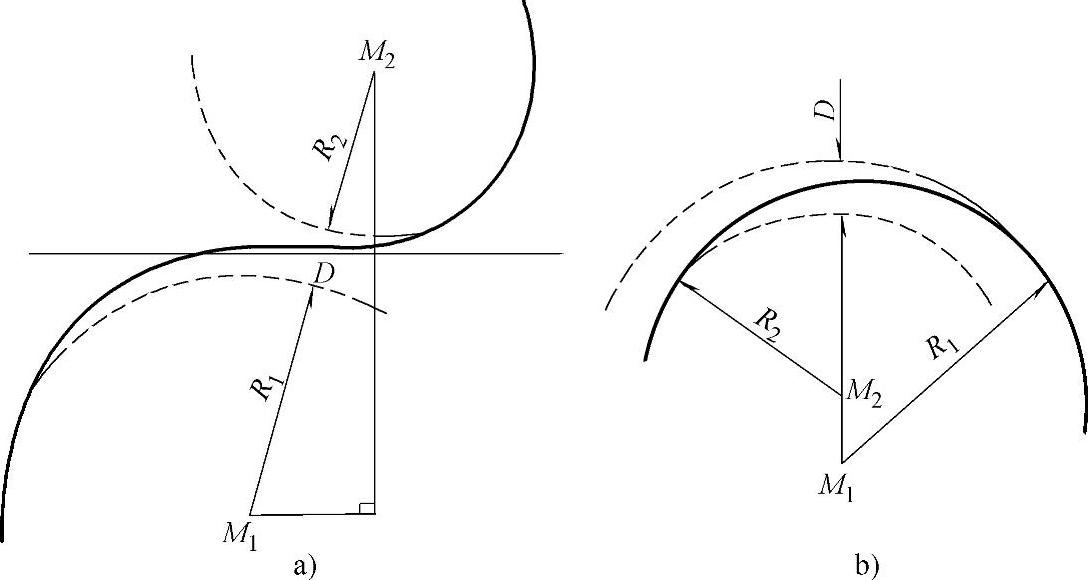
图9-4 S型和卵型曲线计算图

a）S型曲线 b）卵型曲线

①计算两圆间距D。如图9-4a所示，有

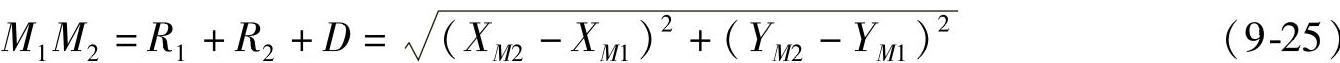
则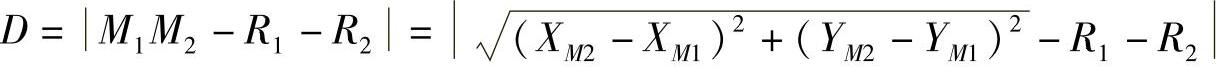

式（9-25）中R₁=R₁，R₂=R₂，下同。(www.daowen.com)

②计算回旋曲线参数。《规范》规定，S型两个回旋线参数A₁与A₂宜相等。当采用不同参数时，A₁与A₂之比宜小于2.0，有条件时应小于1.5。这里用k表示回旋线参数的比值，即k=A₁/A₂。

由几何关系知

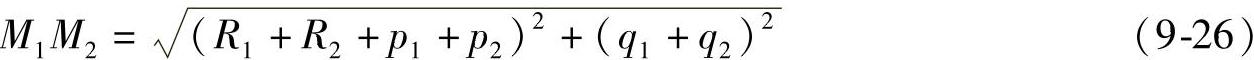
p_i=y_i＋R_icosτ_i－R_i（i=1，2，下同）

q_i=x_i－R_isinτi

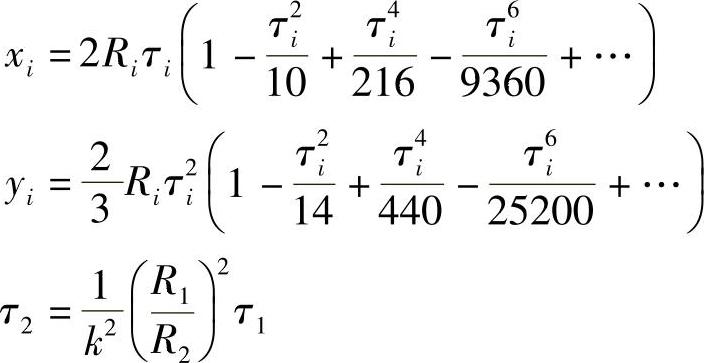
由式（9-25）和式（9-26）可建立含τ₁的方程F（τ₁）=0，解算出τ₁并求得τ₂后按下式计算参数

3）两同向曲线连接。如图9-4b所示，按上述方法求得圆心M₁（X_M1，Y_M1）和M₂（X_M2，Y_M2）坐标后，

同样可建立含τ₁的方程，解算出τ₁后按下式计算τ₂和A

解析法精度高，适用于精细定线，但计算过程复杂，一般可利用计算机进行。

（3）坐标计算 采用曲线型定线法定出的路线平面线形仍然是由直线、圆曲线和回旋线三种线形元素所组成的。当各线形元衔接点的坐标一经确定，路线平面线形的形状和位置便完全确定了。下面分别介绍各种组合线形线元衔接点的坐标和线元上任意点的坐标计算。

1）各线形线元衔接点坐标计算

①直线与圆曲线的连接。如图9-5所示，ZH、HZ点到圆心M的方位角为

α_ZM=α₁＋ξφ₁

α_HM=α₂＋180－ξφ2

式中，，YM=R＋p，q=x－

Rsinτ，。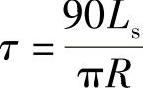

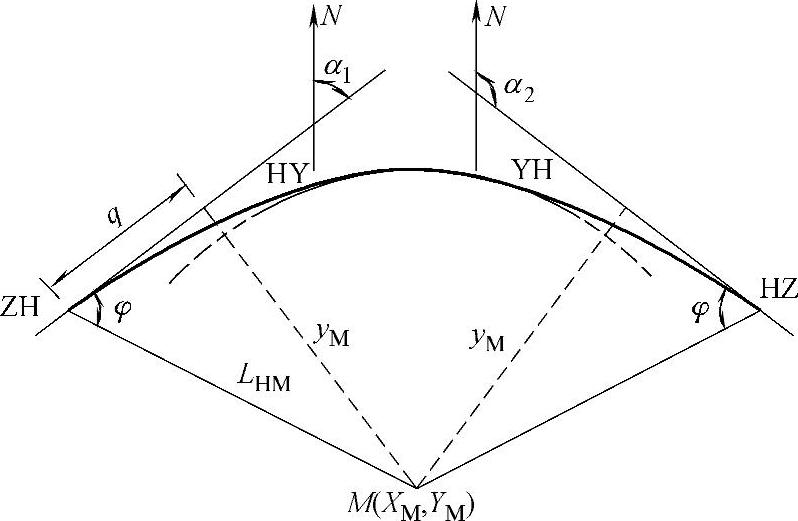
图9-5 直线与圆连接

各衔接点坐标计算式为

式中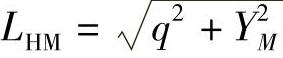

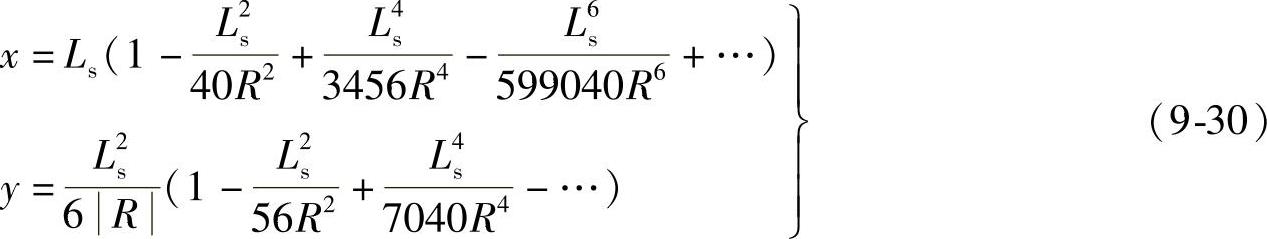
各衔接点的桩号

S_ZH=S₀＋起点至ZH点的距离

S_HY=S_ZH＋L_s

S_YH=S_HY＋L_c

S_HZ=S_YH＋L_s

式中 L_c——HY点至YH点的圆弧长度。

②两反向曲线的连接。如图9-6所示，由几何关系得

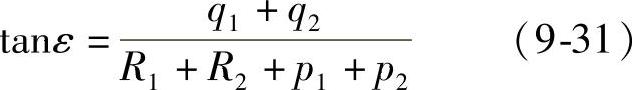
则公切线Q₁Q₂的方位角

α_Q=α_M＋ξ（90－ε）

ξ=SGN（R₁）

衔接点D₁、D₂、D₃坐标计算：

D₂到M₁的方位角α_D2M1=α_Q＋180－ξθ

ξ=SGN（R₁）

Y_M1=R₁＋p₁

D₂点的坐标

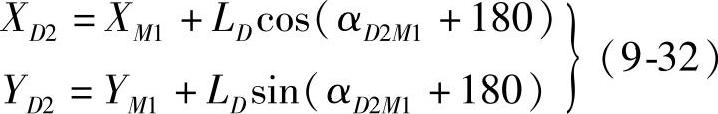
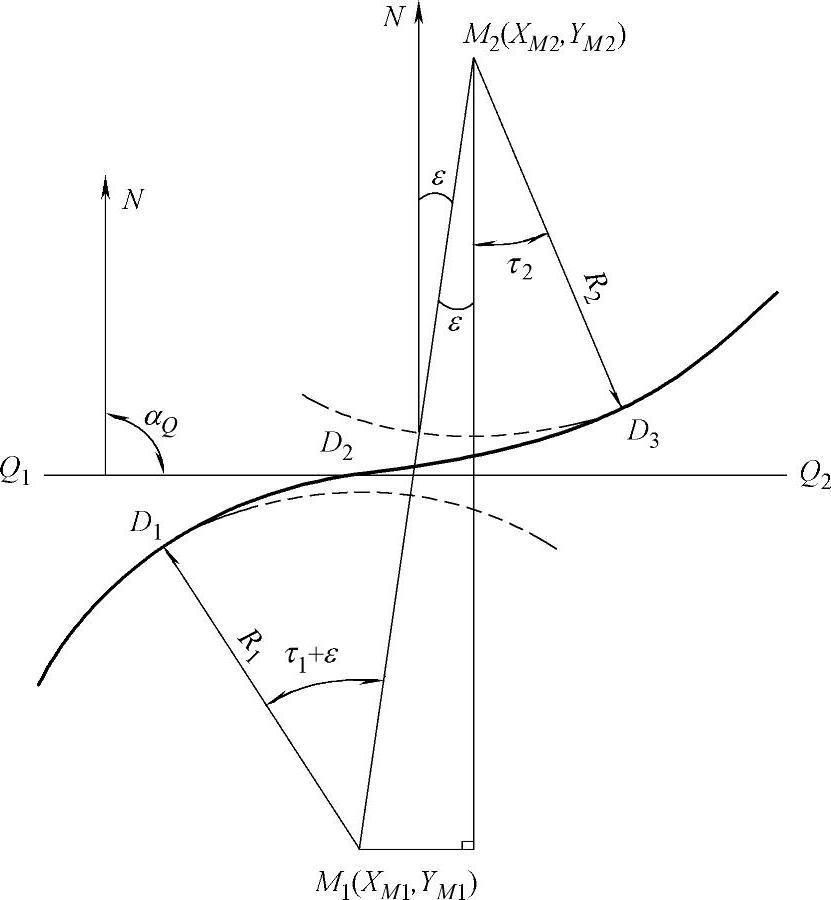
图9-6 两反向曲线的连接

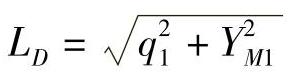
D₁点的坐标

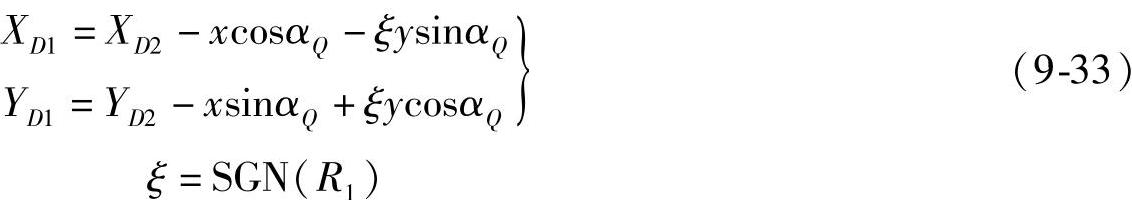
D₃点的坐标

ξ=SGN（R₂），x、y由式（9-30）计算。

③同向圆曲线的连接。由图9-7可知（R₁＞R₂）

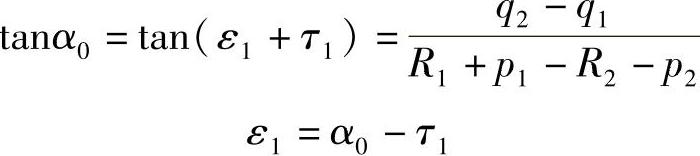
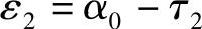
若从大圆过渡到小圆时方位角

α_M1D1=α^－ξ1ε1

α_M2D2=α＋ξ₂ε₂

若从小圆过渡到大圆时方位角

α_M1D1=α＋180－ξ₁ε₁

α_M2D2=α＋180＋ξ₂ε₂

ξ₁=SGN（R₁），ξ₂=SGN（R₂），α为M₁M₂的方位角。

则衔接点D₁和D₂的坐标计算公式为

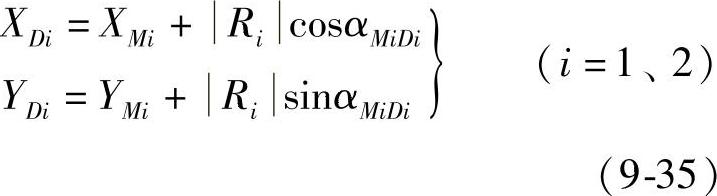
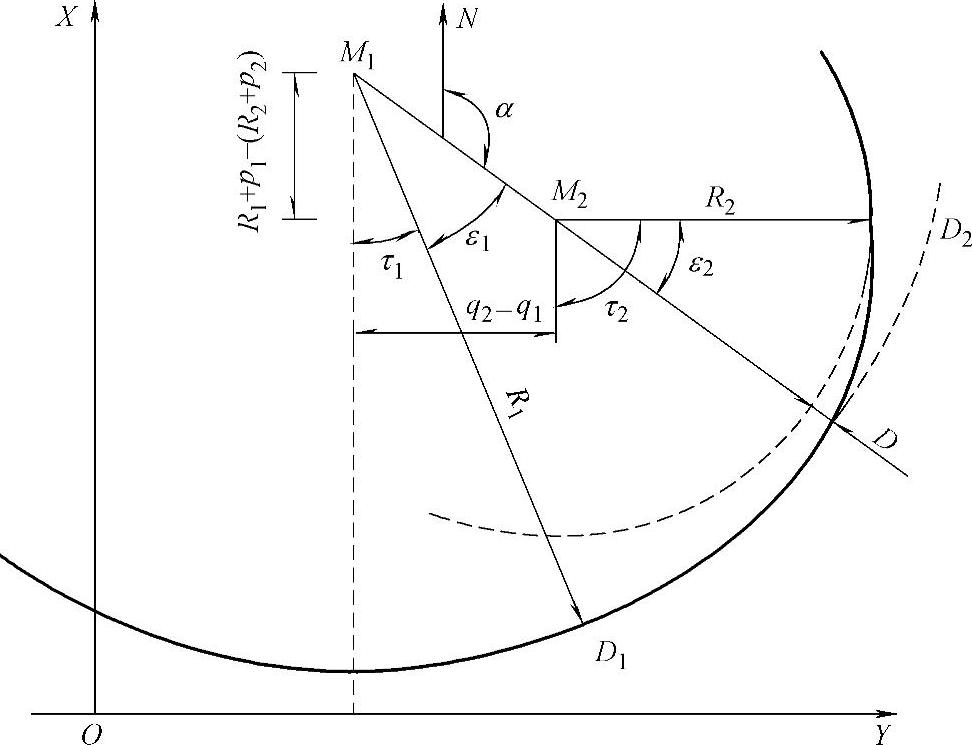
图9-7 同向圆曲线的连接

2）各线元上加桩坐标计算

①直线上加桩坐标。如图9-8所示，设S₀（X₀，Y₀）为直线上已知点，S为任意点桩号，α为该直线的方位角，则

②圆曲线上加桩坐标。如图9-9所示，α₀为S₀点的切线方位角，α为S点的切线方位角，则

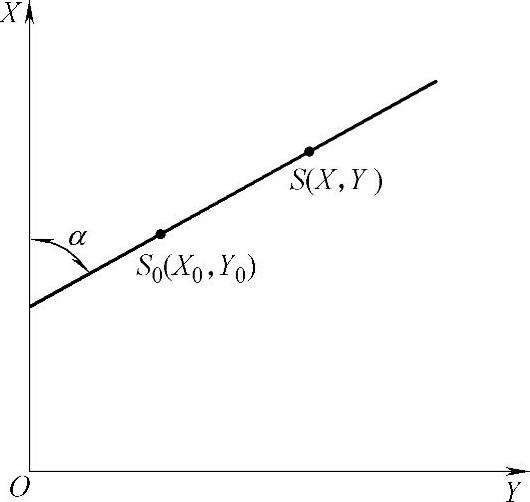
图9-8 直线上点的坐标计算

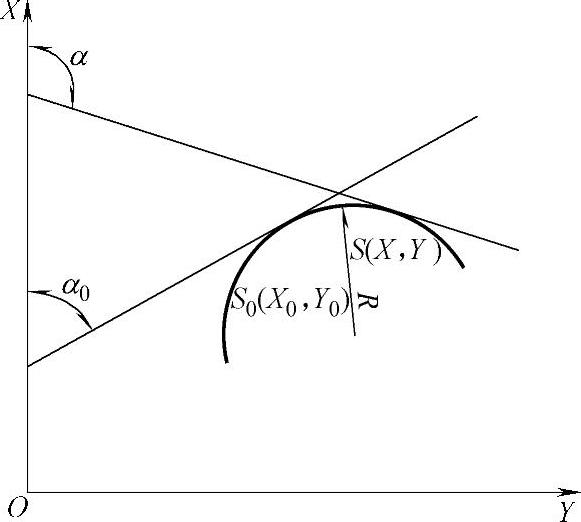
图9-9 圆曲线上点的坐标计算

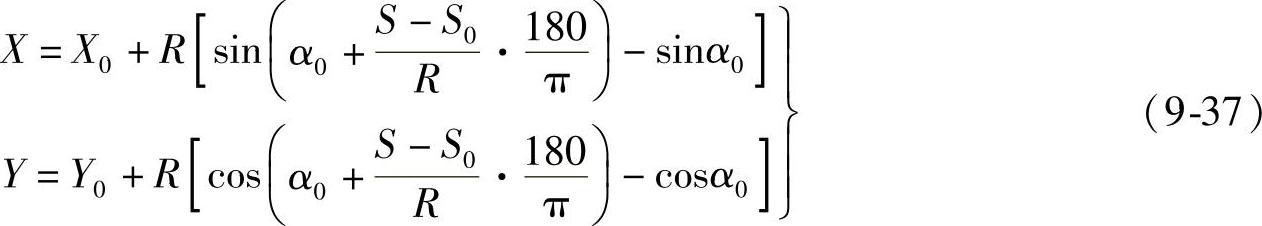
式中 R——圆曲线半径，右转为正，左转为负。

圆曲线上任意点坐标也可以参照式（9-11）、式（9-15）计算。

③缓和曲线上加桩坐标

a.直线与圆曲线连接时，如图9-5所示和式（9-29）可得：以ZH为局部坐标原点时

以HZ为局部坐标原点时

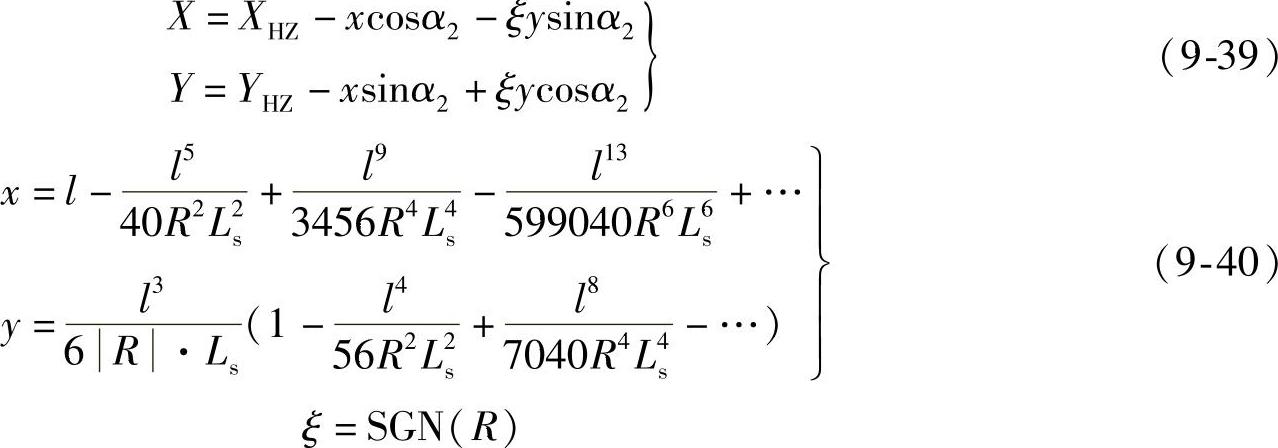
式中 l——缓和曲线上任意点至ZH或HZ点的曲线长。

同样，直线与圆曲线之间的回旋线上任意点坐标也可按式（9-13）和式（9-16）计算。

b.反向曲线连接时。对于反向圆曲线之间的回旋线，如图9-6所示，当公切线方位角α_Q以及拐点D₂（X_D2，Y_D2）确定以后，回旋线上任意点的坐标可参照直线型定线法的有关公式计算。下面介绍另一种计算方法，由式（9-33）和式（9-34）得：

由D₂过渡到D1

由D₂过渡到D3

ξ₁=SGN（R₁），ξ₂=SGN（R₂），x、y按式（9-40）计算。

c.同向曲线连接时。由几何关系得知同向曲线间回旋线长度

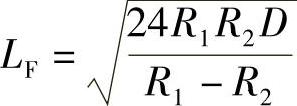
当R₁＞R₂时，如图9-10所示，M₁、M₂以及D₁、D₂的坐标已知，M₁D₁的方位角为α_M1D1，若D1点的切线方位角用α_D1表示，则

α_D1=α_M1D1^＋90ξ

回旋线起点M的切线方位角

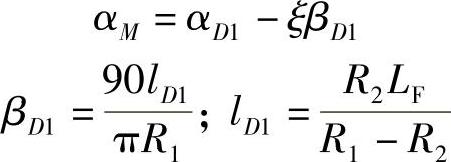
M点的坐标为

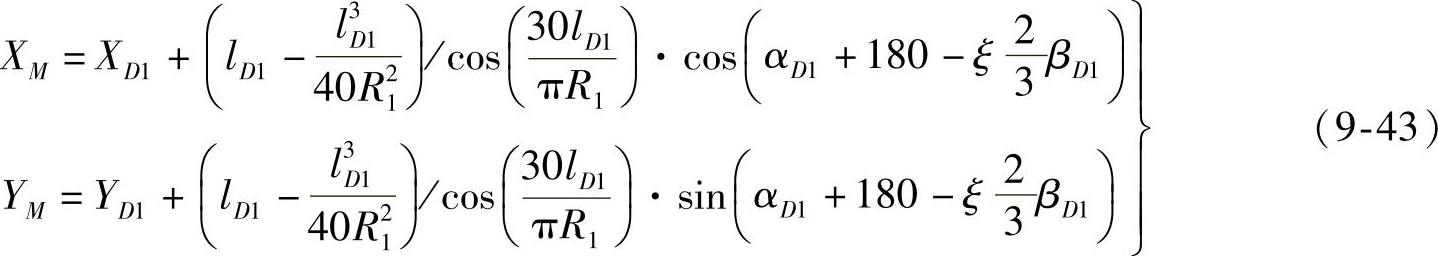
当R₁＜R₂时，如图9-2b所示，M点的切线方位角

α_M=α_D1＋ξβD1

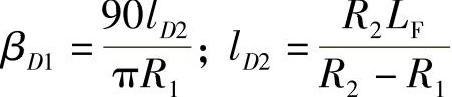
M点的坐标为

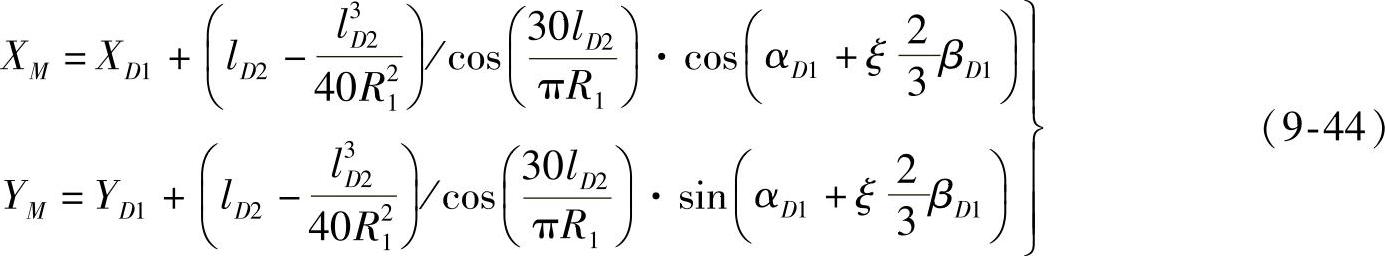
计算出M点的坐标和切线方位角后，当R₁＞R₂时，按式（9-38）计算L_F上计算点坐标，当R₁＜R₂，按式（9-39）计算。

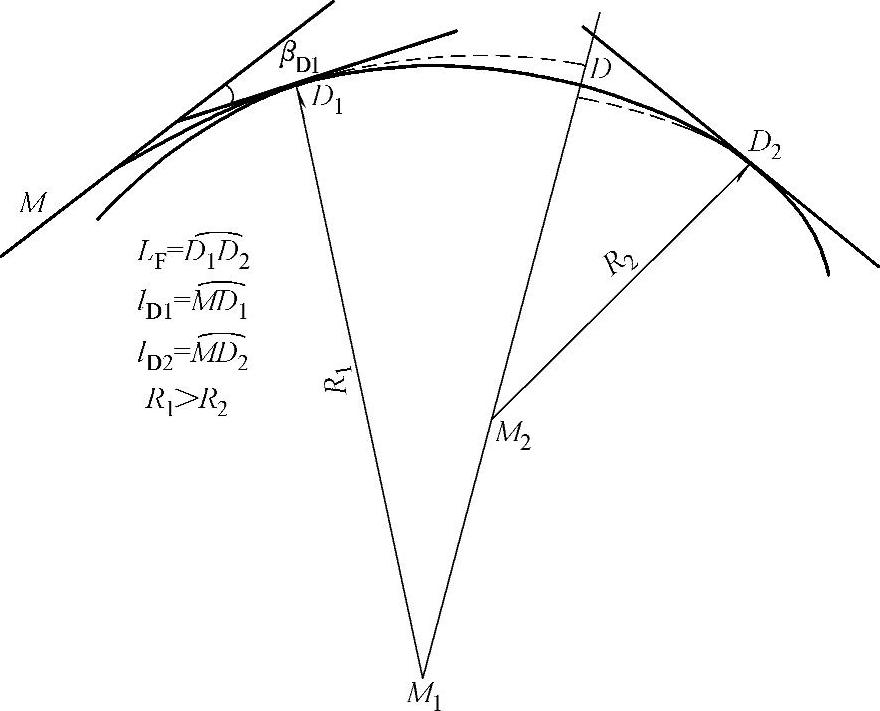
图9-10 同向圆曲线之间的回旋线上点坐标计算