1.用二次抛物线作竖曲线的基本方程

二次抛物线竖曲线如图4-9所示，设变坡点相邻两纵坡坡度分别为i₁和i₂，它们的代数差用ω表示，即ω=i₂－i₁，当ω为正值时，表示凹型竖曲线；ω为负值时，表示凸型竖曲线。

用二次抛物线作为竖曲线的基本方程。在图示坐标系下，二次抛物线一般方程为

对竖曲线上任一点P，其斜率为

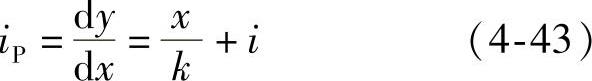
当x=0，i=i₁，x=L时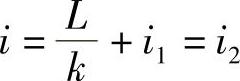，，则

图4-9 二次抛物线竖曲线

抛物线上任一点的曲率半径为

将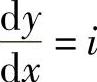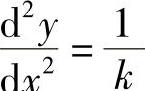，，代入式（4-45），得

R=k（1＋i²）3/2 （4-46）

因为i介于i₁和i₂之间，且i₁，i₂均很小，故i²可略去不计，则

R≈k （4-47）

将式（4-47）代入式（4-42），得二次抛物线竖曲线基本方程式为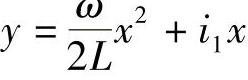或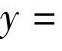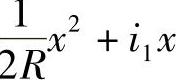，其中，ω为坡差（％）；L为竖曲线长度（m）；R为竖曲线半径（m）。

2.竖曲线要素计算公式

竖曲线几何要素主要有竖曲线切线长T，曲线长L和外距E，由图4-10可得

图4-10 竖曲线要素

竖曲线上任意点竖距y的计算公式为

式中 y——计算点竖距（纵距）；

x——计算点桩号与竖曲线起点的桩号差；

R——竖曲线半径。

3.竖曲线上任意点设计高程的计算

（1）计算切线高程

H₁=H₀－(T－x)i₁ （4-52）

式中 H₀——变坡点高程（m）；

H₁——计算点切线高程（m）；

i₁——纵坡度。

其余符号如图4-10所示。利用该式可以计算直坡段上任意点的设计高程。

（2）计算设计高程

H=H₁±y （4-53）

式中 H——设计高程（m）；

“±”——当为凹型竖曲线时取“＋”，当为凸型竖曲线时取“－”。

其余符号意义同前。(www.daowen.com)

4.竖曲线半径选择因素

1）选择半径应符合表4-15和表4-16所规定的竖曲线的最小半径的要求。

2）在不过分增加土石方工程量的情况下，为使行车舒适，宜采用较大的竖曲线半径。

3）结合纵断面起伏情况和高程控制要求，确定合适的外距值，按外距控制选择半径

4）考虑相邻竖曲线的连接（即保证最小直坡段长度或不发生重叠），限制曲线长度，按切线长度选择半径

5）过大的竖曲线半径将使竖曲线过长，从施工和排水来看都是不利的，选择半径时应注意。

6）夜间行车交通量较大的路段考虑灯光照射方向的改变，使前灯照射范围受到限制，选择半径时应适当加大，以使其有较长的照射距离。

【例4-2】某二级公路上有一变坡点，桩号K10＋200，切线高程为120.28m，两相邻路段的纵坡为i₁=＋5％，i₂=－3％，竖曲线半径R=5000m。试计算该变坡处的竖曲线。

【解】1.竖曲线要素计算

ω=i₂－i₁=－0.03－0.05=－0.08＜0，故为凸型。

曲线长L=Rω=5000m×0.08=400m

切线长T=L/2=400m/2=200m外距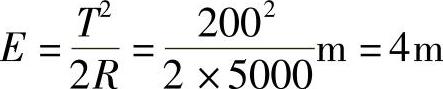

2.求竖曲线起点和终点桩号

1）竖曲线起点桩号：K10＋200－200=K10＋000

2）竖曲线终点桩号：K10＋200＋200=K10＋400

3.求各桩号的设计高程

1）K10＋000竖曲线起点

切线高程120.28m－200m×0.05=110.28m

设计高程110.28m

2）K10＋100处

至起点距离x=10100m－10000m=100m

切线高程110.28m＋100m×0.05=115.28m纵距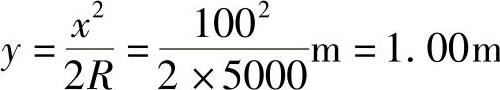

设计高程115.28m－1.00m=114.28m

3）K10＋200竖曲线中点

切线高程120.28m

设计高程120.28m－4.00m=116.28m

4）K10＋300处

至终点距离x=10400m－10300m=100m

切线高程120.28m－100m×0.03=117.28m纵距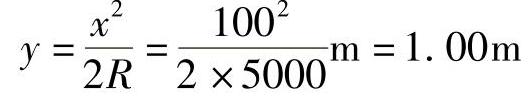

设计高程117.28m－1.00m=116.28m

5）K10＋400竖曲线终点

切线高程120.28m－200m×0.03=114.28m

设计高程114.28m

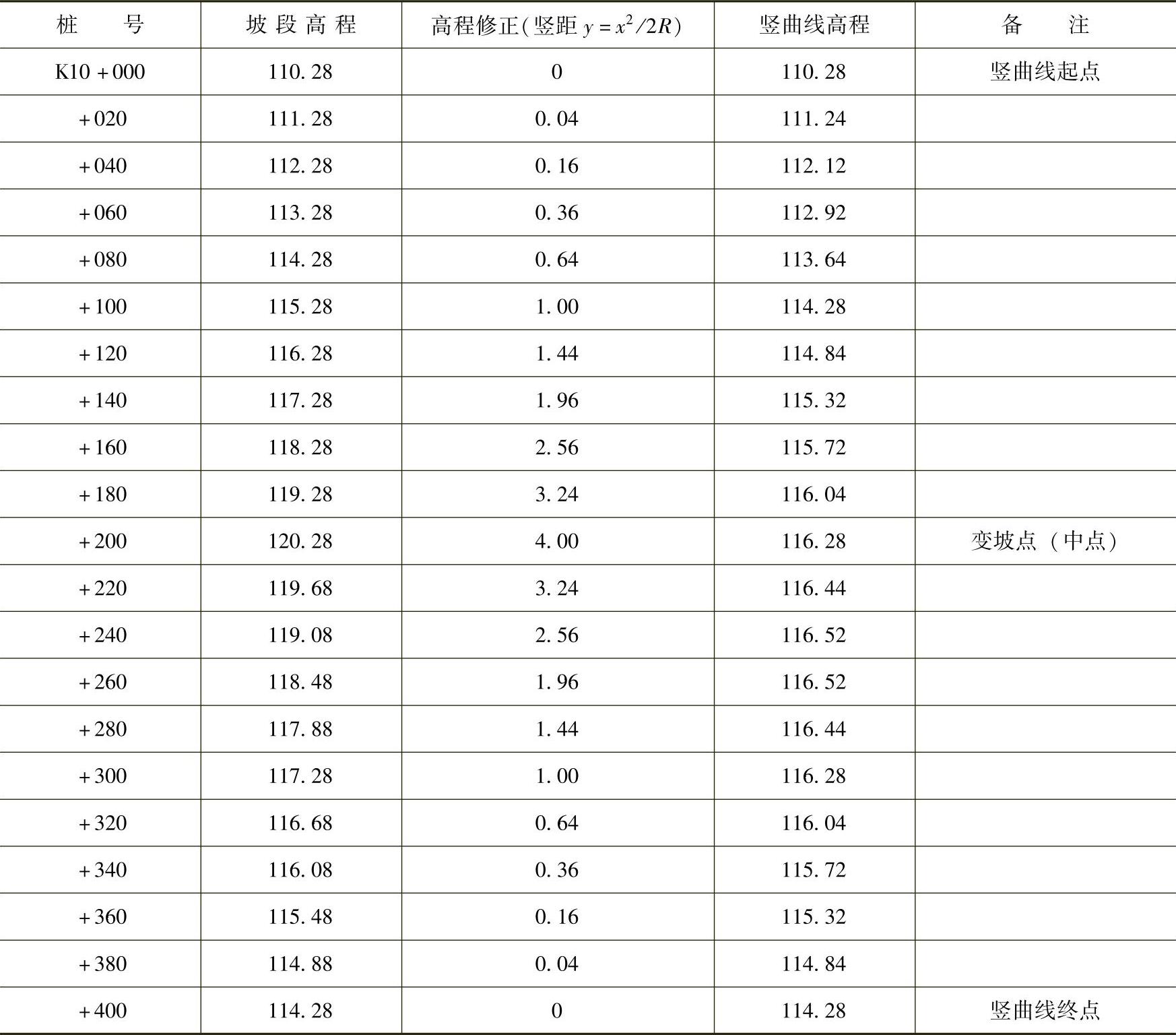
用上法计算得的竖曲线各桩号设计高程见表4-17。

表4-17 竖曲线各桩号设计高程（单位：m）