缓和曲线是设置在直线和圆曲线之间或半径相差较大的两个同向的圆曲线之间的一种曲率连续变化的曲线，是道路平面线形要素之一。在高速公路上由于行车速度高，希望线形能适应汽车在曲线上行驶时曲率渐变的轨迹，所以在直线和圆曲线间及不同半径的两圆曲线间，一般都应设置缓和曲线。在城市道路上，缓和曲线也被广泛地使用。

1.缓和曲线的线形特征

1）缓和曲线的曲率渐变，其线形符合汽车转弯时行驶轨迹的要求；设于直线和圆曲线间，能够消除曲率突变点，使线形顺适、美观，增加道路良好的视觉效果和心理效果。

2）在直线和圆曲线间加入缓和曲线后，平面线形更加灵活，线形的自由度提高，更有利于与地形、地物及环境相适应、协调、配合，使平面线形布置更加灵活、经济、合理。

3）缓和曲线的测设和计算相对于圆曲线更为复杂。

2.缓和曲线的作用

1）曲率连续变化，便于驾驶员操纵方向盘。

2）减小离心力的变换，满足乘客及驾驶员的舒适与稳定。

3）满足超高、加宽的过渡，利于行车。

4）增加平面线形的美观，提高视觉效果和心理效果，如图3-5所示。

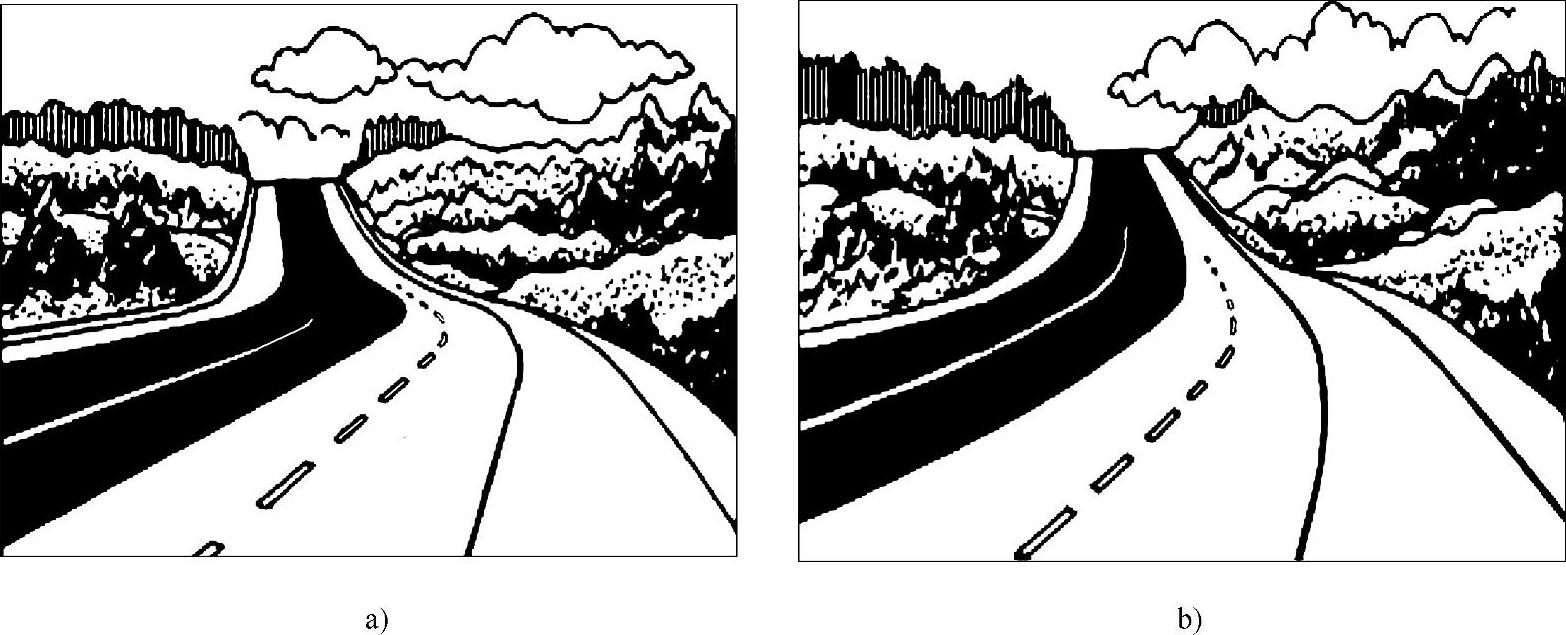
图3-5 直线与曲线连接效果图

a）不设缓和曲线感觉路线扭曲 b）设置缓和曲线后变得平顺美观

3.缓和曲线的形式和计算

缓和曲线的形式有回旋线、三次抛物线、双纽线、n次抛物线、正弦形曲线等。但世界各国使用回旋线居多，《标准》推荐的缓和曲线也是回旋线。而其他曲线的公式较复杂，使用不方便，实际应用极少。

回旋线的特点是曲率半径随曲线长度的增长而减小，即半径r与长度l成反比。基本公式为

ρl=A² （3-2）

式中 ρ——回旋线上任意点的曲率半径（m）；

l——回旋线上某点到原点的曲线长（m）；

A——回旋线参数，表示回旋线曲率变化的缓急程度。

（1）直角坐标计算回旋线上的任意一点的法线方向与Y轴的夹角称为回旋线角，如图3-6和图3-7所示的β。回旋线可用参数β来表示直角坐标，其公式推导如下。

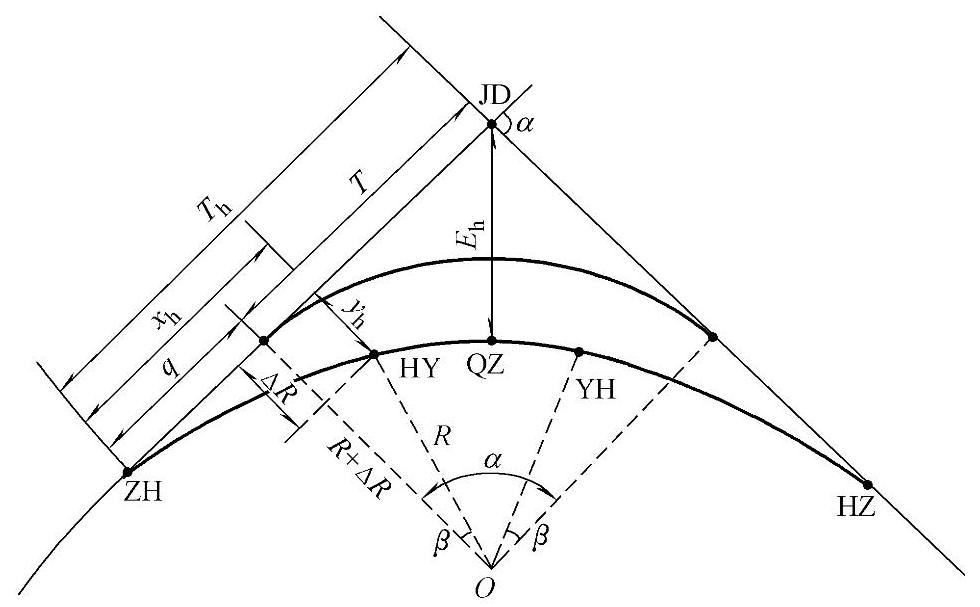
图3-6 有回旋线的平曲线

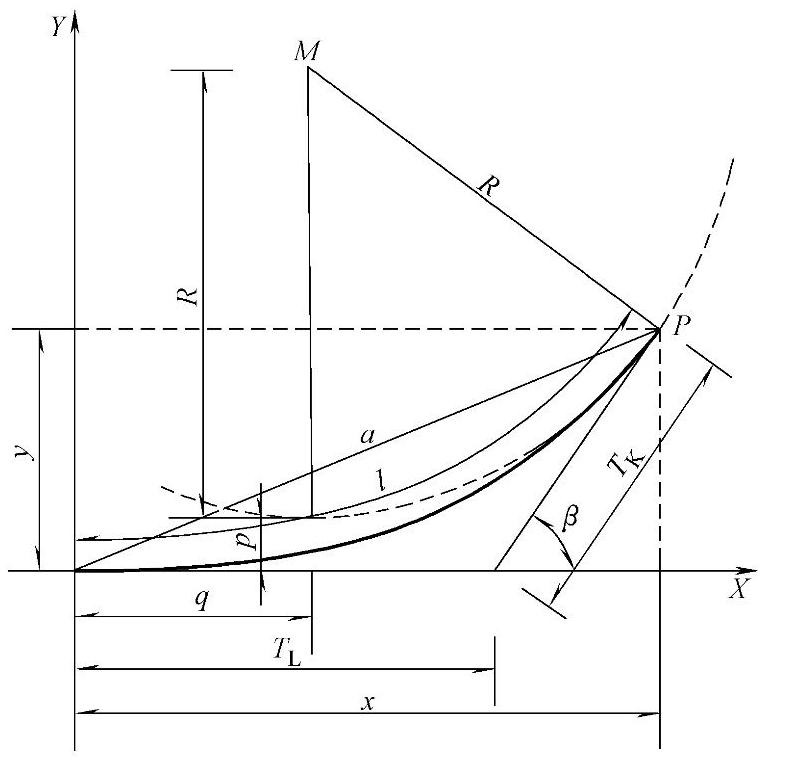
图3-7 回旋线

在回旋线上任意一点P取微分单元，则

dl=ρdβ （3-3）

dx=dlcosβ （3-4）

dy=dlsinβ （3-5）

将式（3-2）代入式（3-3），消去ρ得

对式（3-6）两端积分并整理得

l²=2A²β （3-7）

因β=0时，l=0，积分常数为0，故将式（3-2）代入式（3-7）得

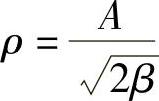
再代入式（3-4）和式（3-6）得

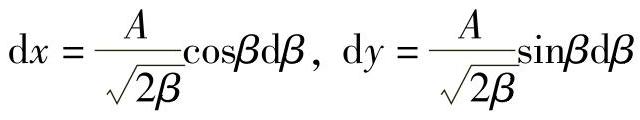
积分得

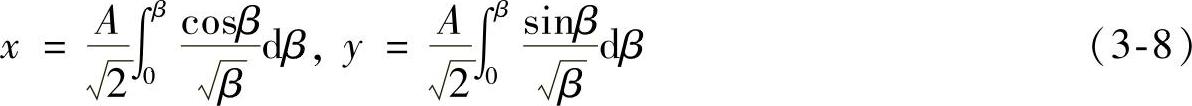
式（3-8）称为菲涅尔积分公式，将sinβ、cosβ用级数展开得

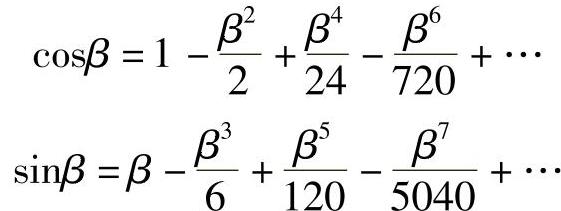
则可得积分

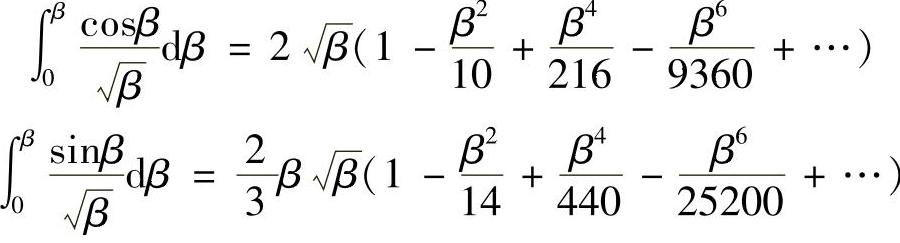
代入菲涅尔积分公式得

将ρl=A²代入式（3-7）得并代入式（3-9）得

Matlab中菲涅尔积分函数形式为，。通过对式（3-8）进行变换最终得到符合Matlab的菲涅尔积分函数形式的公式，即

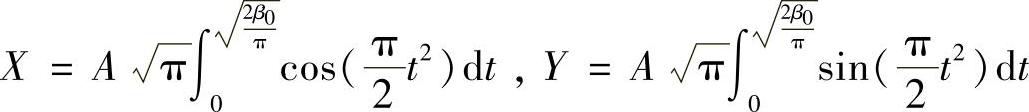
设A分别为100、200和300，β₀分别对应为和30°、45°和180°，用Python对其进行计算和绘图，结果如图3-8所示。

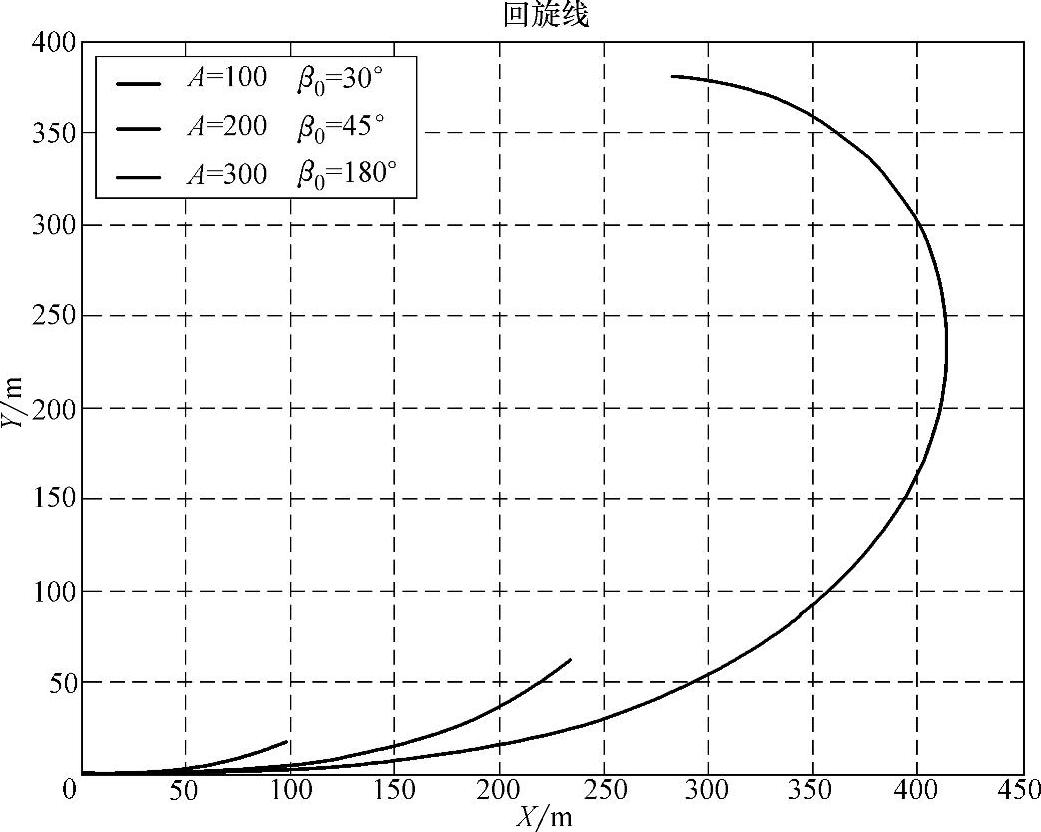
图3-8 回旋线示意图

（2）回旋线曲线要素计算 通过上面的回旋线数学方程、几何关系，通过扩展可以得到不同的回旋线曲线要素的计算公式。

1）任意点P处的曲率半径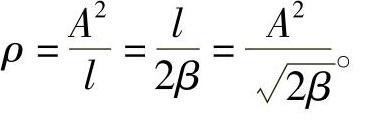

2）曲线内移值Δρ=y＋ρcosβ－ρ。

3）P点瞬时圆心M点的坐标x_M=x－ρsinβ，y_M=ρ＋Δρ。

4）长切线长T_L=x－ycosβ。

5）短切线长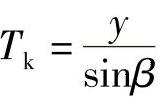

6）P点的弦偏角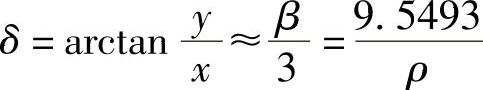。弦偏角也可以定义为回旋线上任意两点间的连线与回旋线半径为无穷大处的切线之间的夹角。

7）P点的弦长。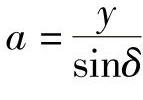

把圆曲线半径R和回旋线参数确定后，即可得到β（以rad计）、ΔR（以m计）、q（以m计）的公式

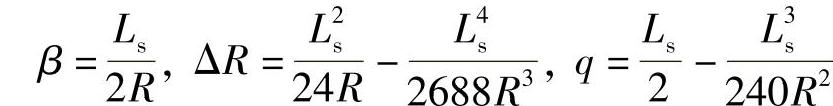(www.daowen.com)

4.带缓和曲线的基本型曲线要素计算

道路平面线形的基本组合为：直线—缓和曲线—圆曲线—缓和曲线—直线，如图3-9所示，其几何元素的计算公式如下

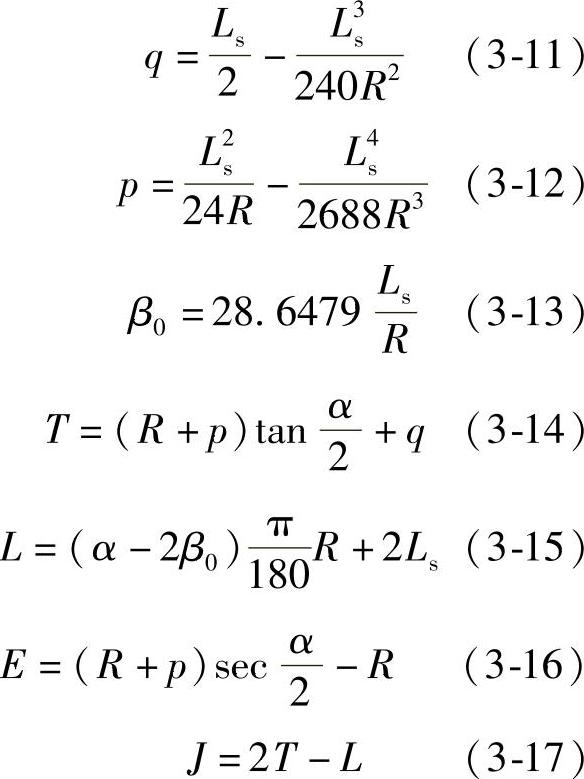
图3-9 中的五个基本桩号的含义如下：

ZH——第一回旋线起点（直缓）；

HY——第一回旋线终点（缓圆）；

QZ——圆曲线中心（曲中）；

YH——第二回旋线终点（圆缓）；

HZ——第二回旋线起点（缓直）。

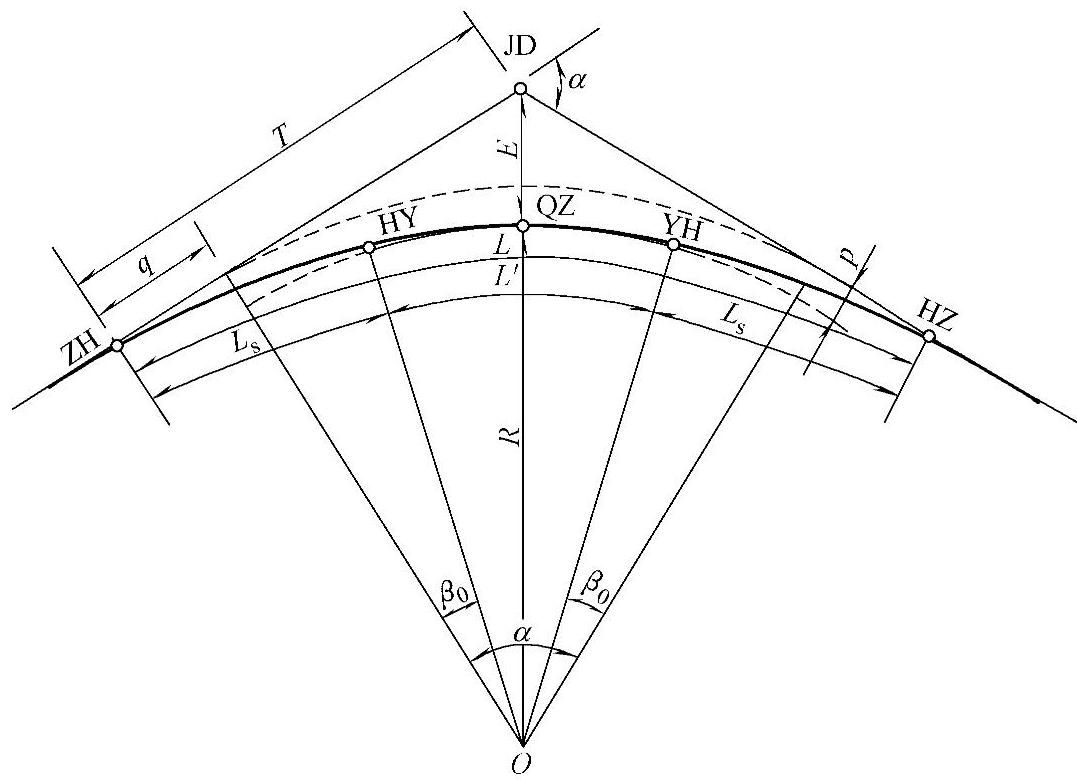
图3-9 “基本型”平曲线

5.缓和曲线的测设

当把缓和曲线设置为回旋线，它的数学计算式推导如下：

在回旋线终点处l=L_s（L_s为回旋线长度），ρ=R，得

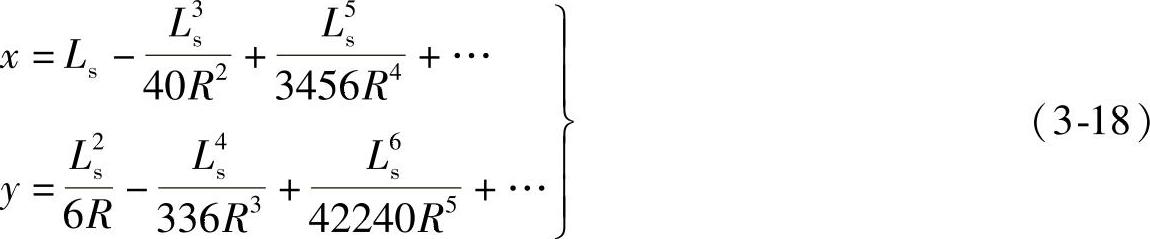
式中 l——回旋线起点至任一点的弧长（m）；

ρ——回旋线上该点的曲率半径（m）；

R——连接回旋线的圆曲线半径（m）。

这种方法即为常用的切线支距法，此时，回旋线上的任一点的坐标即为

相连接的圆曲线按切线支距测定。此时，HY点切线及该点圆心方向即为圆曲线支距测设的坐标轴，以后圆曲线各点位置按圆曲线x、y支距确定。

6.缓和曲线的长度

为使驾驶员操纵方便、行车舒适，以及满足视觉要求，应对缓和曲线长度加以限制。因此，可从以下几方面考虑：

（1）乘客感觉舒适 汽车在缓和曲线上行驶，其离心加速度随缓和曲线曲率变化而变化，若变化过快，将增加驾驶员操作的难度，乘客感觉不舒适，离心加速度的变化率应控制在一定的范围之内。

离心加速度的变化率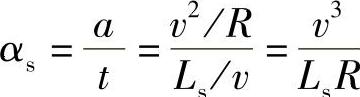

则

选定能保证舒适的最大的α_s，则可得出在一定车速和一定圆曲线半径下的最短缓和曲线长度。一般高速公路，英国采用0.3m/s²，美国采用0.6m/s²，我国一般控制在0.5～0.6m/s²范围内。

若以v（km/h）表示设计速度，则最小缓和曲线长度L_s（min）的计算公式为

（2）超高渐变率适中 一般情况下，在缓和曲线段设有超高缓和段，如果缓和曲线太短则会因路面急剧地由路拱双坡断面变为超高单坡断面而形成一种扭曲的路面。《规范》规定了适当的超高渐变率，由此可导出计算缓和曲线最小长度的公式

式中 B——道路超高横断面旋转轴至行车道路缘带外侧边缘的宽度（m）；

Δi——超高横坡度与路拱横坡度的代数差（％）；

P——超高渐变率。

（3）保证驾驶员操作反应时间 缓和曲线长度应使驾驶员在其上行驶时操作从容，不能过于匆忙，一般情况下以3s行程控制，代入式（3-22）则有

（4）满足视觉要求 根据视觉条件和实践研究可知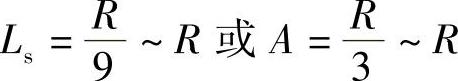：，可以使线形舒顺协调。考虑以上各种因素，JTGD20—2006《公路路线设计规范》（以下简称《规范》）规定了各级公路缓和曲线最小长度，见表3-4。《城市道路工程设计规范》制定了城市道路缓和曲线最小长度，见表3-5。

表3-4 各级公路缓和曲线最小长度

注：“一般值”为正常情况下的采用值；“最小值”为条件受限制时可采用的值。

表3-5 城市道路缓和曲线最小长度

7.缓和曲线的参数A值

缓和曲线参数A值决定了回旋线曲率变化的缓急程度。A_min可根据上述缓和曲线最小长度计算确定。公路平面线形设计时，不仅可以选定缓和曲线长度，同样也可以选定缓和曲线参数A值。

由RL_s=A²可知，进行公路平面线形设计时，可以通过选定缓和曲线长度或选定缓和曲线参数A值的办法，来决定平面线形曲率变化的快慢程度。缓和曲线参数A的最小值应根据汽车在缓和曲线上缓和行驶的要求、行驶时间要求以及允许的超高渐变率要求等决定。

经验认为：使用回旋线作为缓和曲线时，回旋线参数A和与之连接的圆曲线之间只要保持R/3≤A≤R，便可得到视觉上协调而又舒顺的线形。回旋线参数及其长度应根据线形设计以及对安全、视觉、景观灯的要求，选用较大的数值。

但当R在100m左右时，通常取A=R；R＜100m，则选择A=R或A＞R。反之，在圆曲线半径较大时，可选择A在R/3左右；如R＞3000m，即使A＜R/3，在视觉上也是没问题的。

8.缓和曲线的省略

四级公路的直线与小于不设超高的圆曲线最小半径相衔接处，可不设置回旋线，用超高、加宽缓和段径相连接。另外，在直线和圆曲线之间设置缓和曲线后，圆曲线产生了内移值p，在L_s一定的情况下，p与圆曲线半径成反比；当R大到一定程度时，p值甚微，即使直线与圆曲线径相连接，汽车也能完成缓和曲线的行驶，因为在路面的富余宽度中已经包含了这个内移值。所以《规范》规定，在下列情况下可不设缓和曲线：

1）在直线与圆曲线间，当圆曲线半径大于或等于“不设超高的最小半径”时。

2）半径不同的同向圆曲线间，当小圆半径大于或等于“不设超高的最小半径”时，直线与圆曲线间和大圆与小圆间均不设缓和曲线。

3）小圆半径大于表3-6中所列临界曲线半径，且符合下列条件之一时，大圆与小圆间不设缓和曲线。

表3-6 各级公路临界曲线半径

注：1.小圆曲线按规定设置相当于最小缓和曲线长的回旋线时，其大圆与小圆的内移值之差不超过0.10m。

2.设计速度≥80km/h时，大圆半径R₁与小圆半径R₂之比小于1.5。

3.设计速度＜80km/h时，大圆半径R₁与小圆半径R₂之比小于2。

《城市道路工程设计规范》规定的不设缓和曲线的最小圆曲线半径见表3-7。

表3-7 城市道路不设缓和曲线的最小圆曲线半径