汽车在平曲线上行驶时，受到倾向力的作用，如重力、空气阻力的侧向分力和离心力等。汽车在侧向力的作用下，当车轮的侧向反作用力达到附着力时，汽车将沿着倾向力的作用方向滑移；倾向力同时将引起左右车轮法向反作用力的改变，当一侧车轮上的法向反作用力变为零时，则将发生侧向翻车。

1.汽车行驶过程中的横向受力分析

图2-13所示为汽车在有横坡的道路上做曲线行驶时的受力情况。

汽车的总重力G和离心力C作用在汽车的重心C_g上，空气阻力在横向上的分力作用在汽车正面风压中心，其值较小，可忽略不计。此处还有路面对车轮的法向反作用力Z₁、Z₂及路面对车轮的侧向反作用力Y′₁、Y′₂。

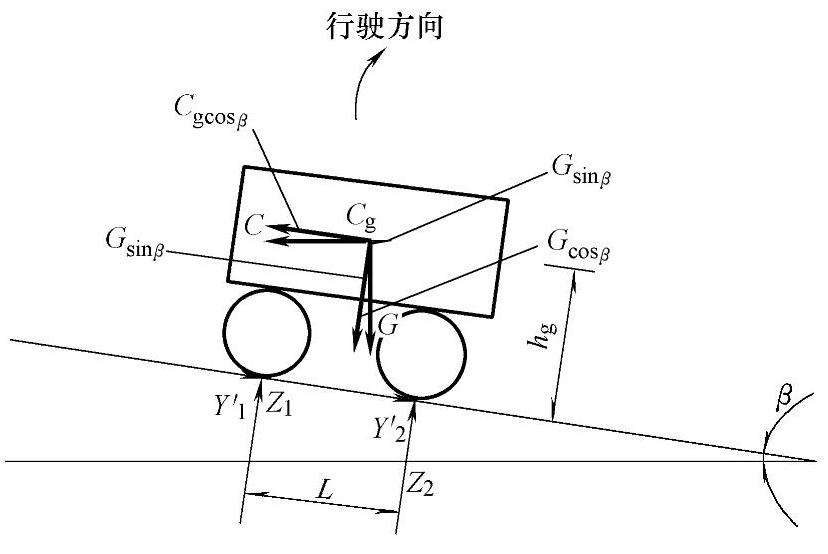
图2-13 汽车在有横坡的道路上做曲线行驶时的受力情况

β—道路横坡角h_g—汽车重心高度B—轮距

（1）法向反作用力计算对汽车的左右轮分别取矩，可得

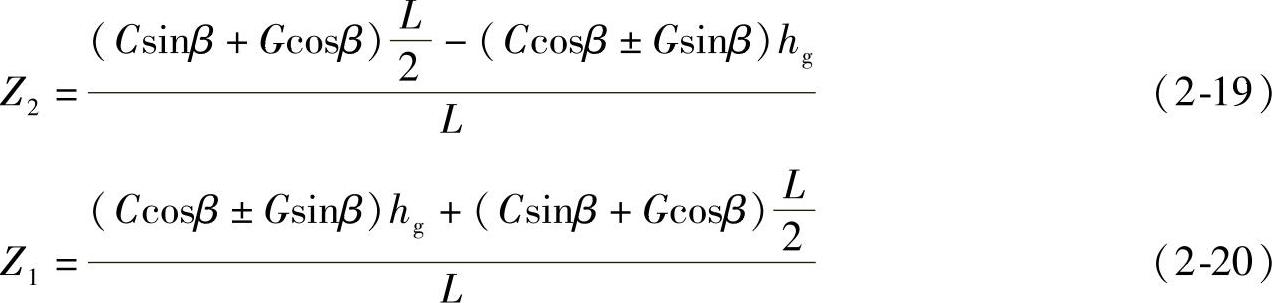
式（2-20）的“±”中“＋”表示重力和离心力在平行于路面方向上的分力同向，即汽车在未设超高的双坡路面外侧行驶；“－”表示汽车在未设超高的双坡路面内侧行驶。

（2）横向反作用力计算由图2-13可以看出，汽车在平曲线上行驶所产生的横向作用力Y为

Y=Ccosβ±Gsinβ

通常β角很小，则cosβ≈1，sinβ≈tanβ=i₀

Y=C±Gi₀（2-21）

式中 i₀——路面横坡度；“±”——意义同前。

离心力C由计算式为

式中 v——汽车行驶速度（m/s）；

g——重力加速度（m/s²）；

R——道路平曲线半径（m）。

将C的计算式代入式（2-21）中，则

由于汽车横向稳定性不取决于Y的绝对值而决定于汽车单位质量的相对横向力，称横向力Y与车重的比值为横向力系数_μ，即

由式（2-24）可得

(www.daowen.com)

式（2-25）即为公路平面设计中圆曲线半径的计算公式及已知半径条件下的限速计算公式。注意：式（2-25）中的“＋”、“－”的意义与前述意义相反，即汽车在双坡路面外侧行驶时，采用“－”，在双坡路面内侧行驶时采用“＋”。

（3）侧向反作用力路面对于车轮的侧向反作用力Y′（Y′=Y′₁＋Y₂′），受路面附着条件的限制，其最大值为

Y_m′_ax=Gφ_r

式中 φ_r——横向附着系数。

当汽车在平曲线上行驶时，作用在车轮上的力，不仅有切向牵引力F_t，还有横向力Y，此时车轮与路面接触面上形成一个总反作用力P′，P′的极限值为

P′_max=Gφ

同理，牵引力F_t的极限值为F′_tmax=Gφ_χ

式中 φ_χ——纵向附着系数。因F′²_max=F′²_tmax＋Y′²max故

φ²=φ²_χ＋φ²_r（2-26）

分析式（2-26）可知，横向附着系数φ_r的取值，要受汽车行驶状态（即切向牵引力F_t的大小）的限制，当无切向力而有横向力时，φ_r取极限值φ；当无横向力而仅有切向力，φχ取极限值φ；当两个方向都受力时，φχ、φ_r均不能采用极限值，而是当附着力用于切向部分大一些时则用于抵抗横向力部分就小一些，反之亦然，这是受总附着力限制的结果。根据实验与经验，一般采用φχ=（0.7～0.8）φ，φ_r=（0.6～0.7）φ。

2.横向倾覆

在倾斜的坡面上做曲线运动的汽车，由于横向力的作用，当位于曲线内侧车轮上的法向反作用力为零时，汽车将发生横向倾覆。对图2-13中所示的车辆，N_r=0为汽车发生倾覆的临界状态，由式（2-19）得

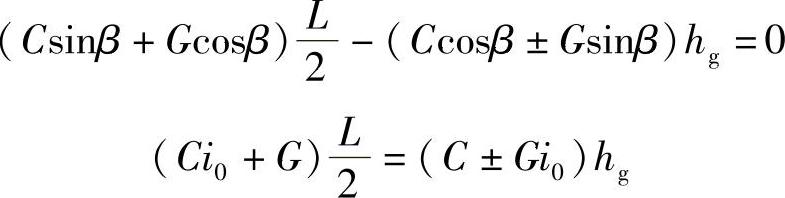
由于Y=C±Gi₀，并考虑Ci₀与G相比，其值很小可忽略不计，则上式可简化成

根据上述分析可知，当_μ＞L/2h_g时，汽车将发生横向倾覆。而μ值与R和v有关。将式（2-27）代入式（2-25）中，可得出R为定值时，为保证不发生横向倾覆，汽车行驶的最大速度v_max以及当v为定值时，平曲线所能采用的最小曲线半径，即

3.横向滑移

汽车在平面上行驶的时候，即存在着使汽车向外侧滑移的横向力Y，同时也存在着阻止汽车向外侧滑移的横向反力Y′。横向反力Y′受附着条件的限制，即横向反力Y′_max=Gφ_r。当横向力Y大于附着力Y′时，汽车将发生横向滑移，由平衡条件可知Y=Y′_max=Gφ_r，则

μ=Y/G=φ_r （2-29）

即当_μ＞φ_r时，汽车将发生横向滑移，将式（2-27）代入式（2-25）中，可得出当R为定值时为保证不发生横向滑移，汽车能行驶的最大速度，以及当v为定值时，平曲线所能采用的最小曲线半径，即

4.抵抗横向倾覆与横向滑移的比较

比较式（2-27）和式（2-29），倾覆与滑移现象哪个先出现取决于L/2h_g和φ_r的数值，若L/2h_g＞φ_r，则滑移先于倾覆出现，反之则结果相反。

现代汽车由于轮距较宽，重心低，一般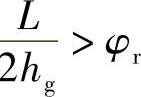（通常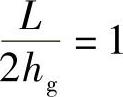，而φ_r＜0.5），所以出现滑移的现象先于倾覆。在公路设计中，若能保证汽车不滑移（μ＜φ_r），则同时也就保证了倾覆的稳定性。但必须注意，若长途客车在车顶上行李装载过重或载重汽车装货过高，此时重心提高，也有可能首先出现倾覆现象，故一般对装载高度应有所限制。