在实际海洋中,波浪是随机的,也就是说,在一定的时间及地点,波浪的出现及其大小,完全是一个随机现象,无法预知。从数学上讲,它属于随机范畴,应该采用概率统计的方法加以分析。以波高为例,通过每次观测,可测到一个确定的结果,但每次观测的结果彼此是不相同的,是随时间随机变化的。这种变化必须用随机函数,也叫随机过程,加以描述。
随机过程有各种不同的类型,在海浪研究中,应用最广泛的是平稳随机过程,它的特点是过程的统计特征(平均振幅、反差等)不随时间坐标原点的推移而变化,即某时刻t的统计特征与时刻(t+τ)相吻合。此外,在一般情况下,海浪作为一个随机过程具有各态历经性,由于各态历经性,过程中的每一个变量的期望值,与其沿时间的平均值相等,即一个充分长时间的现实能代替同一时段现实的总体。
海洋中的不规则波可看作是一个平稳的各态历经的随机过程,因此可在一个样本中任取足够长的一段,即可分析得到总体的时域特性和频域特性。
波浪的尺度常用波高、周期表示。对于不规则波形,通常采用上跨(或下跨)零点法。以上跨零点法为例,取平均水位为零线,把波面上升与零线相交的点作为一个波的起点。波形不规则地振动降到零线以下,接着又上升再次与零线相交,这一点作为该波的终点(也是下一个波的起点)。如横坐标轴是时间,则两个连续上跨零点的间距便是这个波的周期;若坐标轴是距离,则此间距是这个波的波长。把这两点间的波峰最高点到波谷最低点的垂直距离定义为波高。对于中间可能存在的小波动,只要不与零线相交即不予考虑。
按上跨零点法从图7.2的波浪记录上读得各个波高和周期,列入表7.1中,可见各波高值相差很大(表中n表示波高大小的次序)。为了描述图7.2的波浪系统,一般采用两种方法:一是对波高、周期等进行统计分析,采用有某种统计特征值的波作为代表波浪的特征波方法;二是用波浪谱表示。下面依次介绍这两种方法。
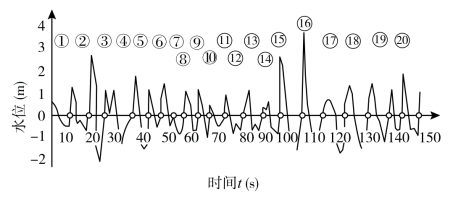
图7.2 波浪观测记录实例(按上跨零点法定义波浪)
表7.1 波浪数据记录表
对于特征波的定义,欧美国家多采用部分大波的平均值法,俄罗斯等采用超值累计率法,我国两者兼用。通常采用大约连续观测100个波作为一个标准段进行统计分析。
1.按部分大波平均值定义的特征波
(1)最大波
Hmax、THmax:波列中波高最大的波浪和相应于最大波高的周期。例如表7.1中的第16个波,得Hmax=4.9m、THmax=8.0s。THmax表示相应于最大波高的周期,以下依次类推。
(2)十分之一大波
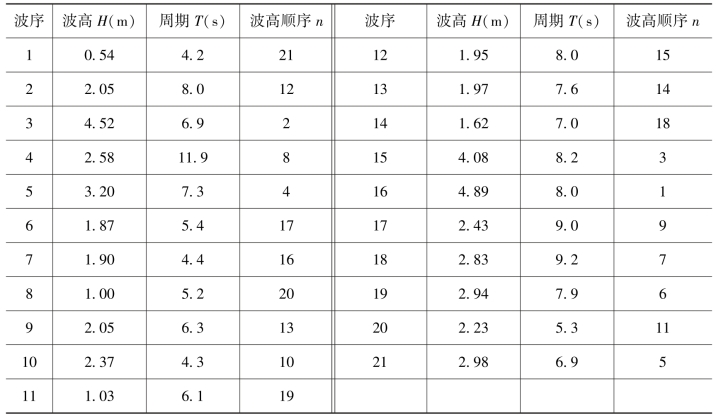
H1/10、TH1/10:波列中各波浪按波高大小排列后,取前面![]() 个波的平均波高和平均周期。表中十分之一大波为16与3的均值,得H1/10=4.7m、TH1/10=7.5s。
个波的平均波高和平均周期。表中十分之一大波为16与3的均值,得H1/10=4.7m、TH1/10=7.5s。
(3)有效波(三分之一大波)
H1/3、TH1/3:按波高大小次序排列后,取前面![]() 个波的平均波高和平均周期。表中波系有效波为16、3、15、5、21、19和18号波的均值,得H1/3=3.6m、TH1/3=7.8s。
个波的平均波高和平均周期。表中波系有效波为16、3、15、5、21、19和18号波的均值,得H1/3=3.6m、TH1/3=7.8s。
(4)平均波高和平均波周期
波列中所有波高的平均值和周期的平均值。

式中,H =2.4m;![]() =7.0s。
=7.0s。
(5)均方根波高Hrms

式中,Hrms=2.66m。
这些特征波中最常用的是有效波,西方文献中泛指海浪的波高、周期时多指有效波(H1/3、TH1/3)。
国际水利研究协会(IAHR)编写的波浪要素参数表统一了不规则波浪的术语、定义和符号。建议采用H1/3,u和H1/3,d分别表示按上跨零点法和下跨零点法定义的有效波高,其余类推。本节采用上跨零点法。为简便计,故符号中均略去下标u。
2.按超值累积概率定义的特征波
常用的有H1%、H5%、H13%。以H1%为例,其定义是指在波列中超过此波高的累积频率为1%。其他特征波的定义可依次类推。
上述各特征值可由对实测资料进行统计分析予以确定,大波特征值和累积特征值可以相互转换,H13%约相当于H1/3;H1/10约相当于H4%。
3.波高分布
根据朗吉特-希金斯对于窄谱波分析,对于深水波,波列中的波面振幅a具有瑞利(Rayleigh)分布,其分布函数为

式中,ση为波面坐标的方差。
利用求原点矩的方法可得平均振幅![]() 的表达式为
的表达式为

由H=2a,![]() 与上两式可求得平均波高表示的波高理论概率分布函数为
与上两式可求得平均波高表示的波高理论概率分布函数为
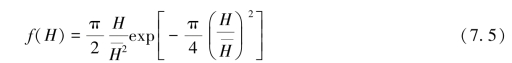
式中,![]() 为平均波高。(https://www.daowen.com)
为平均波高。(https://www.daowen.com)
相应的波高累积频率(简称累计率)函数F(H)为

常用的累积频率波高HF与平均波高关系可根据上式得到,分别为

对于深水波,常用的部分大波的平均波高Hp与平均波高关系为

当波列足够长,即N足够大时,最大波高的数学期望值![]() 为
为

对于波周期,一个波列也有相应的波周期的分布和相应的T、T1/10、T1/3和Trms等特征值。Hmax与Tmax不一定对应在同一个波上,同样H1/10也不一定对应T1/10。因为在同一个波列中,最大波高的波,其相应的周期不一定最长,最小波高的波,其周期不一定最短,这从表7.1的记录中也可以发现。但在一般应用中,往往将它们配对使用。
4.海浪谱理论简述
上述的海浪统计规律只能反映出波浪的外在特征,而难以描述波浪的内部结构。为了进一步了解海浪特性,便引进了“谱”的概念。海浪谱可以用来描述波浪的内部结构,说明波浪内部由哪些部分组成及其内在关系。当然,波浪的内部结构与其外在表现是有关联的,也正因为海浪的内部结构复杂,使其外在表现千变万化。
20世纪50年代初,郎吉特-希金斯用莱斯(Rice)分析电子管噪声电流的方法,将无限多个不同振幅、频率和初始相位的余弦波叠加起来描述某一固定的海面,即
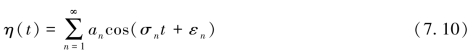
式中,an,σn分别为第n个余弦组成波的振幅和圆频率;εn为第n个波的初相位角,εn为一个均匀分布于0~2π的随机量。
如果将频率介于σ~σ+Δσ范围内的各组成波的振幅平方的一半叠加起来,并除以包含所有这些组成的频率范围Δσ,其结果将是一个σ的函数,令它为S(σ)(有些书中用S(f)表示,S(f)=2πS(σ)),则有

由于一个组成波平均波能为

则全部组成波的总能量为
![]()
式(7.13)的含义相当于Δσ时间间隔内全部组成波的能量和(差一个乘积常数ρg),故S(σ)相当于单位频率间隔内的平均波能量,称为波能密度。海浪的总能量由所有组成波提供,函数S(σ)给出了不同频率间隔内组成波提供的能量,因此实际函数S(σ)就相当于波能密度相对于组成波频率的分布函数,这一函数称为波频谱,通常简称为频谱。由于它反映了波能密度分布,所以又称为能谱。
图7.3是一个波频谱的示意图,其横坐标为频率σ,纵坐标为波能密度S(σ)。可以看出,在σ=0附近,S(σ)很小,随着σ增大,S(σ)先是急剧增大,增到最大值后又迅速地减小,最后又趋近于零,S(σ)最大值相应的频率称为谱峰频率σp。理论上S(σ)分布于σ=0~∞之间,但其显著部分集中于一狭窄的频域内。这是因为当频率很大时,波周期很小,波长很短,其所含的能量也很小,因此以重力波为主体的实际海浪中,常表现为窄谱波。
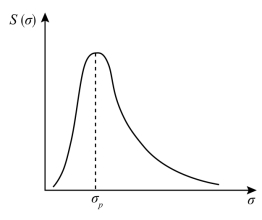
图7.3 波频谱
以叠加手段确定的波频谱,只能描述某一固定的波面,不能反映波浪内部相对于方向的结构,也不足以描述大面积内的波面。因为在实际的海浪中,引起某一固定点海面波动的一个波列,总有一个主要的传播方向,但其构成除了有沿主波向的组成波外,还有许多其他不同方向的组成波。为了描述这种波列,可将无穷多个振幅为an,频率为σn,初相为εn并沿着x,y平面上与x轴成θn角方向传播的组成波叠加起来,即
![]()
和前面一样,可定义
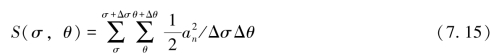
式(7.15)表示频率在Δσ间隔范围和方向在Δθ间隔范围内各组成波提供的能量的平均值,故函数S(σ,θ)相当于波能密度相对于组成波的频率和方向的分布,这是一种二维谱。给定频率时,S(σ,θ)描述不同方向间隔的能量密度,因而它是反映海浪内部方向结构的能谱,通常称为方向谱(图7.4)。
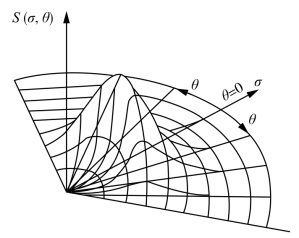
图7.4 方向谱
方向谱对于研究海浪预报、波浪折射、绕射、波浪作用下泥沙运动等具有重要意义。方向谱一般可写成如下形式:
![]()
式中,G(σ,θ)为方向分布函数。
方向分布函数表示海浪能量在不同方向上的分布状态,频率不同,能量相对于方向的分布形式亦有不同。
波频谱的形状与波浪的生成机理有关,主要决定于风速、风距和风时3个要素,目前世界上常用的这类谱有PM谱、Brestchneider谱、联合北海波浪计划(JONSWAP)谱等。此外,也可以根据海区的实测波浪资料(波向和波周期)来求得适合于当地条件的谱,例如我国《海港水文规范》(JTS 145—2—2013)中提出的海浪方向谱,其表达式为:
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








