潮汐理论一般只能给出海洋潮汐现象变化的基本规律和特点，想准确地了解具体海区潮汐的大小及其变化规律仍然必须进行实际观测。根据实际观测资料进行潮汐分析，以便求得潮汐调和常数。由潮汐调和常数可以了解分潮波组成的大小，而且可用来推算潮汐和为潮波数值计算提供依据。

潮汐调和分析就是以潮汐静力学为基础，根据潮汐观测资料进行分析，计算潮汐调和常数的过程。

1.实际潮汐分潮

在实际潮位中，直接由引潮力作用所产生的分潮叫做引力潮或天文潮，通常它是水位变化的主要成分。除此之外，还存在气象分潮、天文-气象复合潮和浅水潮，它们和天文潮一起构成了潮位中的可预报部分。主要由气象扰动引起的水位不规则变化叫做噪声，它引起分析结果的误差。

现有的潮汐分析方法有很多，它们差不多都能得出同样好的结果。但基于最小二乘法原理得出的方法具有最大的灵活性。这里需要指出，无论采用哪一种方法，在选取分潮时，必须使之与观测时间间隔及观测时段长度相适应，否则就不能得出良好的结果，甚至不可能得出结果。

对于一年时间的观测记录，只能从中分离出不同亚群的分潮。因此，对于在同一亚群之中的分潮，必须引入它们之间已知的推算关系。传统的做法是利用交点因子和交点订正角，用以考虑同一亚群中次要分潮对主分潮的影响。

引潮力可以展开成许多余弦振动之和。虽然不能期望实际海洋的潮汐与有平衡潮理论所得出的结果一样。但可以期望，在某一个频率为f＝σ/2π的周期性变化的引力潮分潮(包括垂直和水平引潮力)的作用下，海洋也要产生这一频率的振荡。在某一地点，海面高度变化应包含有这个频率的成分，可以写作Hcosα，它代表了实际潮汐的一个分潮，其中振幅H对一定地点为常量，位相α以速率σ均匀增加。

既然实际分潮位相α的增加速率与引潮力相角的增加速率相同，则α将与引潮力相角保持着不变的位相差。当然，可以将α与垂直引潮力相应分潮的相角进行比较，也可以与水平引潮力或平衡潮的相应分潮的相角进行比较。在潮汐分析和预报工作中，习惯于与垂直引潮力或平衡潮的相角(这两者相位相同)进行比较，并规定k为地方迟角

式中，v为当地垂直引潮力的位相。k之所以被称为迟角是因为正如它为正，则当地垂直引潮力分潮最大，即当v＝0时，α为－k，需要再经过k/σ这样一段时间，α才能达到0°，亦即实际潮汐分潮才能达到最大。所以，k反映了实际分潮相对于天文分潮的位相落后。

k是由把当地实际潮汐分潮位相和当地天文分潮的相角相比较而得出的，它的物理意义较明显，早先的潮汐文献中多采用这种迟角。但在实际工作中采用它会不方便，因为这样做必须对每个不同经度的地方计算该处的天文相角。现在在实际潮汐分析和预报中，更多地采用另一种迟角，其规定是这样的:实际潮汐观测所用的时间是区时，例如用东N区时，在这个时间系统的tN时刻，设实际分潮的位相为αN，而在格林尼治的tG＝tN时刻，若格林尼治天文角为vG，则取迟角

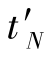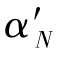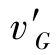这样，以后作预报时，如欲知道观测站在N区时时刻的实际分潮位相，可用格林尼治的天文分潮相角减去g得到。这样就不必推算当地的天文相角，格林尼治天文相角可以直接用于任何地点。在这里，等式tG＝tN只是数字上相等，它们实质意义上不是同一时刻，在格林尼治到达tG时刻要比在东N时区到达tN时刻迟N小时。

为了建立g和k的关系，要弄清式(5.4)和式(5.5)之间意义上的差别。在式(5.5)中，实际分潮和天文分潮的位相的比较是在同一时间系统中进行的，也就是说，k是天文分潮和实际分潮在同一瞬间的位相之差。所谓同一瞬间的意思就是在同一时间系统中的同一个时间值。由于位相差不随时间变化，所以时间系统可以随便选用，不一定要用地方时，所要强调的是对天文分潮和实际分潮要用同一个时间系统。而式(5.5)中，天文和实际分潮的位相则分别采用不同的时间系统:实际分潮采用区时，天文分潮采用世界时。还不只是如此，天文分潮用的不是相对于观测地点的相角，而是用相对于格林尼治的相角。这样一来，由于格林尼治tG时刻要比在数值上与之相等的东区N区时的tN时刻落后N小时，故在格林尼治tG时刻，实际分潮的位相已不是αN，而是αN＋σN。而在格林尼治tG时刻，位于东经L处的观测地点的天文相角则是vG＋μL。如前所述，迟角k与所用的时间系统无关，现在αN＋σN和vG＋μL都是在同一时间系统(世界时)中同一时刻(tG)的观测地点的实际分潮和天文分潮的位相，故两者之差为k

k＝vG＋μ1L－(αN＋σN)＝vG－αN＋μ1L－σN

将式(5-5)代入，便得k和g之间的换算关系:

注意，式中L和N系指东经和东N时区，若是西经或西N区时，则其值为负。

下面将用格林尼治迟角称呼g。

还有一些早期的文献可能会采用区时迟角k′，它与k不同之处在于以标准子午线处的v值代替同一时刻观测地点的v值。由于在同一时刻s，h′，P，N′，p′均相同，只有平太阴时角相差ΔL＝L－15°N，故有

代入式(5.6)，可得k′和g之间的换算关系:

在式(5.7)和式(5.8)中，采用的角度单位是度，若以弧度为单位，则式中15°应改作π/12。

在近代文献中，已经很少有人再采用k′作为迟角。

由于迟角k与所用的时间系统无关，故在资料中不需要注明采用的时间系统。而对迟角g情况就不同。凡是资料中用了迟角g，就必须注明所用的时区。如果某处的一组调和常数，观测时采用了东N′时区，算得的迟角为g′，现在想把它化到东N区时下的迟角g，则可用

计算这个式子很容易由式(5.6)得出。因为k值与时间系统无关，故有k＝g＋μ1L－σN，又有k＝g′＋μ1L－σN′，两式相减即得式(5.9)。例如，已知在琉球群岛许多岛屿上的调和常数，它们所采用的时区为东9时。为了与我国沿海的调和常数作对比，希望对它们也采用东8时区，则由于此时式(5.9)中N－N′＝－1，应当把琉球群岛在东9时区下的g值都减去相应分潮的σ值。

H和g(k和k′)叫做实际潮汐分潮的调和常数，它们反映了海洋对这一频率外力的响应。这种响应决定于海洋本身的动力学性质。由于海洋环境的变化十分缓慢，对一般海区，调和常数具有极强的稳定性，在不特别长的时期内，可充分近似地认为是常数。只有在那些短期内地形具有重大变化的地点，调和常数才显示出随时间有明显可感觉到的变化。

上面谈的是某一个周期的引潮力引起的海面升降。事实上引潮力是由许多不同周期的振动叠加起来的，因而实际海面升降也是由许多不同周期的振动叠加而成的。故应当用下式表示潮位高度:

但更经常地，将用

来表示潮高。式(5.11)中v要理解为格林尼治天文相角，为了省略，这里和以后都不加下标。v0为t＝0时刻的v值。上两式中S0均为长期平均水位高度。

迟角的负值－gi代表了实际分潮相对于引力分潮的位相超前，而实际分潮对引潮力分潮的振幅比Hi/Ci代表了实际分潮相对于引潮力分潮的放大率，它们一起代表了观测地点对频率fi＝σi/2π的周期性外力的响应特性。把它们看作频率的函数，就叫做响应函数。实际潮汐的响应函数通常是比较平滑的。

2.调和常数

k是天文分潮和实际分潮在同一瞬间的位相之差，所谓同一瞬间就是指在同一时间系统中的同一个时间值。由于位相差不随时间变化，所以时间系统倒是可以随便选用，不一定要用地方时，所要强调的是对天文分潮和实际分潮要用同一个时间系统。

还有一些早期的文献可能会采用区时迟角k′，它与k的不同之处在于以标准子午线处的v值代替同一时刻观测地点的v值。

H和g(k和k′)叫做实际分潮的调和常数，它们反映了海洋对这一频率外力的响应。这种响应决定于海洋本身的动力学性质。

3.准调和分析

如果观测的时间长度只有一天或几天，则叫作做短期观测。这时只有少数几个主要分潮的调和常数可以由观测数值直接确定；对其余的分潮必须引进与这些主要分潮的一定的已知关系。

如果利用电子计算机分析，可以直接采用调和分潮方法，也可以事先把调和分潮合并成少数准调和分潮。但如手工计算，则只能采用准调和分潮方法。(www.daowen.com)

(1)准调和分潮

能够互相分离的分潮之间的最小频率间隔与观测时段的长度有关，当分潮之间的会合周期显著大于观测时段长度时，则必须引入已知的关系。本章所要分析的观测数据的时段只有一天或几天，这就需要进一步引入不同分潮之间的关系。

以一个分潮为主，对其余分潮的调和常数给出它们与这个主要分潮调和常数的一定关系，这实际上相当于把这些分潮合并到主要分潮而成为一项。但这一项的振幅和角速率不再是常量，而是随时间作缓慢变化(如果被合并的分潮之间的角速率相近的话)，因而称这样的项为准调和分潮。

如果要分析的观测数据只有一天，则对每个潮族只能允许有一个主要分潮，若观测数据是若干组一天观测的资料，则可以允许每个潮族有少数几个主要分潮，但是一般不能由这类观测数据求得长周期分潮的调和常数。

杜德森等曾经根据实际潮汐的特点，把所有较大的全日潮合并成O1和K1两个分潮；把所有较大的半日分潮合并成M2和S2两个分潮。如果观测数据不少于两天，这4个分潮的调和长数都能计算出来，但如果只有一天的观测数据，需要在这两对分潮之间进一步引入一定的关系。杜德森给出的准调和分潮的振幅和位相的计算公式比较粗略，下面给出的公式是根据方国洪(1974，181b)“潮汐分析和预报的准调和分潮方法”。

引潮力的第二项展开式如下:

式中，头两项是长周期项，不能考虑，最末一项比例与sin4，只有最大项(第六项)的0.2%，把它略去。这样，剩下的有5项。对太阳引潮力也有相应的5项。此外，辐射潮S2也有一定的量值。至于引潮力中与月地或日地距离四次方以上有关的次要项，由于它们很小，将其略去。这样，剩下的总共有11项，每一项叫做一个分潮，它们的振幅(略去公共因子)记作W，相角记作μ115°t－ω。相角中时间t是从深夜零时起算的，单位为小时，因此15°t即等于式(5.12)中的平太阳时角T加上180°。每个子分潮中包含的主要调和分潮的频率，可以把它们合并为O1，K1，M2和S2。下面以O1为例说明对实际分潮进行合并的有关问题。O1系数为

天文相角μ115°t－ω＝15°t－(2λ－h′＋v－2ξ＋90°)；O1子分潮展开后，包含着O1，Q1，ρ1等许多纯调和分潮。不需要具体将其展开式写出，而只要给出如下一个形式上的表达式

这里W代表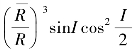，ω＝2λ－h′＋v－2ξ＋90°，σ的单位是度/小时。假定右边展开式中，当i＝1时为O1调和分潮。上式也可写为

其中，

由此可得

与式(5.13)右边引潮力调和相应的实际调和分潮为

将这些分潮都合并到第一个，即O1分潮。如果调和常数之间满足下列关系:

其中A为常量，这时式(5.17)中振幅便可写作Hi＝，位相则为

故式(5.17)转化为

若式(5.16)右边t以t－A代替，则所得的W和ω值便是t－A时刻的值，可记为Wt－A和ωt－A，即

将其代入式(5.20)，便得

若记

则有

与天文情况有关的变量D和d分别叫做准调和分潮的振幅系数和迟角订正。

已经看到，引潮力的一组调和分潮可以通过式(5.14)由一个引潮力准调和分潮代表；相应地，一组实际调和分潮也可以通过式(5.24)由一个实际的准调和分潮代表。而且，如果条件(5.19)满足，实际准调和分潮的振幅和相角与A小时前的引潮力准调和分潮相应量有关，与其余时刻，特别是与当时的引潮力则没有关系。故A叫做这个准调和分潮的潮龄。

对O1的合并过程，显然完全适用于M2。对K1和S2也可类似地处理，只是这时子分潮不只是一个，而是若干个，因而与式(5.16)相对的等式的左边应当有若干个Wcosω和Wsinω之和。

(2)D和d计算公式

现在给出O1，K1，M2和S2各准调和分潮D，d值的实际计算公式。由于这些变量变化不十分迅速，一般只对零时直接用后面给出的公式计算，对其余间，可由零时的值内插得出。

基本天文元素s，h′，p，N′，p′的计算公式如下:

式(5.25)的含义是，为计算某一天t时的天文变量D和d值，需要以这时刻前A小时来取代这个时刻。潮龄A可以有两种基本的取法，一种是对O1，K1，M2和S2各自取值，这样做要准确一些。但如要计算某一个时刻的D和d值，必须计算4组不同的基本天文元素。另一种是取全日潮的视差潮龄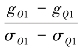(如海区以全日潮为主)或半日潮视差潮龄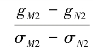(如海区以半日潮为主)来代替所有4个分潮的潮龄。因为在所有被合并掉的分潮中，Q1和N1是做主要的分潮，所以着重考虑它们。同时由于这两个分潮是由月地距离的变化，亦即月球视差的变化引起的，故这种潮龄反映了实际潮汐落后于视差变化的时间间隔，称为视差潮龄。

知道了基本天文元素后，下一步可计算I，v，ξ，λ和，公式如下:

这样，潮位的6个准调和分潮的表达式为:

式中，X0代表平均海面高度加上长周期分潮；D和d可有国家海洋局科技情报研究所1979年出版的《天文变量表》查出，该表列出了1979—1999年每天零时的O1，K1，M2，S2，M4和MS46个分潮的D和d值。

式(5.27)中各准调和分潮的D和d值是随时间而变化的。特别是d值变得较快，这是由于相角被写成μ115°t－d－g的形式，但t前面的系数并不代表分潮真正的角速率。准确的角速率应当是μ115°－d·，这里d上面的黑圆点代表对时间的导数。这个角速率本身也是随时间变化的。但是由于每个准调和分潮中以与其同名的调和分潮占优势，故这个角速率只在同名的调和分潮角速率上下作不大的变动，且其平均值等于后者。因此在较短的时间内，例如一天之内，可以将潮位h近似表示为几个调和项之和:

式中，(C＝O1，K1，M2，S2，M4和MS4)为此期间中间时刻的DC值；＝dc－(μ115°－σc)(对O1和K1，μ1＝1；对M2和S2，μ1＝2；对M4和MS4，μ1＝4)，dc为的dc值。与式(5.27)相比较，可知用该式代替式(5.27)时，在中间时刻t，各分潮的振幅和相角完全相同，当t≠但t－t的量值不大时，其误差亦不大。有时为方便起见，也可取，的数值等于与最接近的一个零时的D，d值。这种取法意味着当t＝0时各分潮的振幅和相角与式(5.27)相同，而当t≠0时，有不大的误差。

用准调和分潮表达式(5.27)比用调和分潮表达式要简单得多，不但可以简化许多分析过程，而且在分析某些实际潮汐特征时也能使得问题变得更容易。但它之所以能代替调和分潮表达过程，完全依赖于式(5.18)假设。这一假设在深海中常能得到较好满足；在浅水海区中，许多浅水分潮不能被包括进去，从而导致一定误差。