众所周知，太阳、月球与地球的相对运动是引起海面周期性涨落的根本动因。尽管太空中的其他星体也对地球产生引力作用，但相对于太阳和月球的影响几乎可以忽略，通常只考虑月球和太阳对地球的引潮作用。

引起潮汐的原因是很复杂的，主要是由月球和太阳“引潮力”引起的。在介绍引潮力之前，首先以月球引潮力为例，阐述引潮力的两个构成因素:月球引力和离心力。

第一个构成因素是月球的引力。万有引力定律告诉我们，宇宙中一切物体之间都是互相吸引的。月球对地球存在着引力，在地球上不同的地方，月球的引力是方向不同、大小不等的。引力的方向指向月球中心，引力的大小因地球上各地距月球中心的距离而不同。如图5.1所示，月球直射点B，距月球中心最近，引力最大，A点和C点次之，B点的对跖点D处，月球的引力最小。

第二个构成因素是地球绕地月公共质心转动而产生的离心力。由于月球对地球有引力，地球对月球也有引力，在地月之间就构成了一个互相吸引的引力系统，并有一个公共质心，位于距地心0.73乘以地球半径的地方。地球除一刻不停地进行着自转和绕日公转外，还要绕地月公共质心转动，产生离心力。这股离心力刚好和月球对地心的吸引力大小相等、方向相反，使地月之间能够保持一定距离。这种情况就好比用绳子拴住一块石头使其转动，石头受到人手对它的拉力，在转动时产生了离心力，与该拉力正好平衡。由于地球在绕公共质心运动时，地球上各点之间处于平动状态，所以在地球上的不同地方，这股离心力是方向相同、大小相等的。

月球引力和地球离心力是两种对立的力，两者结合起来产生的合力(矢量和)，就是月球使海水发生潮汐现象的力量，称为“月球引潮力”。月球引潮力在地球不同地方各不相同。在面向月球的直射点B，引力大于离心力，两者合成的引潮力，使海水向上(向月球方向)运动，造成涨潮。在背向月球的对跖点D，离心力大于引力，两者合成的引潮力，也使海水向上(背向月球方向)运动，也造成海水上涨现象。在A点和C点，引力和离心力合成的引潮力向下(向地球中心)，使海水向下运动，造成海水下降现象。在地球自转过程中，地球表面上任何一点，都有经过类似A、B、C、D 4个位置的机会，因此在一个太阴日内常见的潮汐有两涨两落的现象。

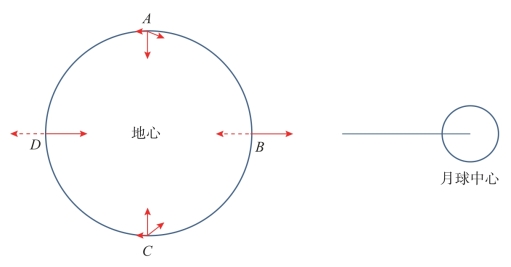
图5.1　地球受月作用示意图

实际上，引潮力是月球和太阳对地球的引力，以及地球绕地月公共质心旋转时所产生的惯性离心力，这两种力的合力，它是引起潮汐的原动力。

引潮力的实质究竟是什么?它是怎样产生的?要回答这些问题，首先需从天体引力谈起。绕转着的天体，都受到两种力的作用，一种是绕转天体间的引力，一种是由于绕转而产生的离心力。两种力同时作用，才使天体能够维持其按一定规律绕转的运动状态。月和地球绕转、地和日绕转也是这样。

引力和离心力，对于整个天体来说，两者是保持平衡的。但是，对于天体上的每一个质点(位于天体中心的质点除外)来说，两者是不平衡的。绕转天体之间的引力同绕转运动所产生的惯性离心力的不平衡，是产生引潮力的根本原因。

太阳和月球对地球的引力，地球在绕转中产生的离心力，以及由于这两种力在地球表面所表现出的不平衡，其本质是相同的。由月球作用而产生的潮汐，称太阴潮；由太阳作用而产生的潮汐，称太阳潮。太阳潮和太阴潮并无本质上的差异，但在量值上，太阴潮大于太阳潮。

引潮力在地球上的分布是不均匀的。各地点引潮力大小、方向的差异，必然使被海水所覆盖的地球变形。以正垂点为中心的半球，引潮力的水平分力指向正垂点，另一个分力指向月球(或太阳)，海水质点向正垂点方向集中、朝向月球(或太阳)隆起；以反垂点为中心的半球，引潮力的水平分力指向反垂点，另一个分力背向月球(或太阳)，海水质点向反垂点方向集中、背向月球(或太阳)隆起；在这两个半球交界的地方，引潮力指向地心，海水质点向下移动。这样，就使完全被海水覆盖的地球，变成一个分别朝向和背向月球(或太阳)隆起的扁球体。正垂点和反垂点的连线，就是这个扁球体的长轴。这种由于引潮力作用而产生的变形，称为潮汐变形。

在地球上看来，在引潮力作用下，以正、反垂点为中心的海水朝向和背向月球(或太阳)隆起，都是海面的向上升高，在正、反垂点周围，各形成一个水位特高的地区，叫做潮汐隆起；在距正、反垂点最远的地方，指向地心的引潮力使那里的海面下降，形成水位特低的地带。(www.daowen.com)

以正垂点为中心的潮汐隆起，称为顺潮，它始终朝向月球(或太阳)；以反垂点为中心的潮汐隆起，称为对潮，它始终背向月球(或太阳)。因此，随着月球(或太阳)自东向西的周日视运动，两个潮汐隆起不断地自东向西移动，一日之内在地球上移动一周。距正、反垂点最远的海面最低地带，也相应地在地球上自东向西移动。这样，在地表某个具体地点所看到的情况，就是随着时间的流逝，海面不断上升，达到最高水位后，又不断下降，降到最低水位后，又开始上升如此不停地循环往复，这就是海面不断涨落的周期性运动。

就地球潮汐而言，水质点受到的最主要的是月球和太阳的引力，其他星球由于距离太远或者由于质量小，其吸引力都很小，可以略去不计。与此类似，把月球换成太阳，产生的周期性作用力就是太阳引潮力。

月球引潮力在量值上等于月球对地球单位质量物体的引力与月球对地心单位质量物体的引力(即月球对地球单位质量物体引力的平均值)之差。

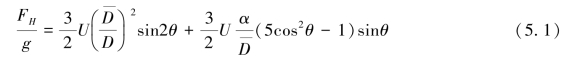
式中，U为常数，其值为:

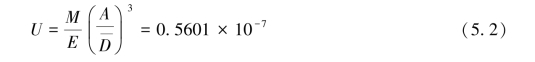
式(5.1)即为地球表面的引潮力公式，其中为月球距离D的平均值。式(5.1)中等号右边的第一项叫做引潮力的主要项，第二项叫做次要项，它只占第一项的1/60左右，只有很小的实际意义，而前面省略的项则还要更小。

上式对太阳引潮力也完全适用，只要将式(5.1)、式(5.2)中的M，D，θ换作S(太阳质量)，R′(日地距离)，θ′(太阳天顶距)就可以了。

而

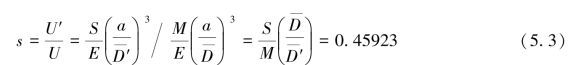
式(5.3)表明，太阳引潮力略小于月球引潮力的一半。可见，对于潮汐现象而言，月球的作用是主要的。