施工中隧道的轴线并不是完全为光滑的曲线，实际上是通过一系列等距离坐标点拟合而成，一般每隔1 m取一个点即可满足施工精度的要求。整条隧道的轴线一旦确定，则根据隧道设计轴线的方程可以生成所有拟合点的坐标，将这些点的坐标值存储在计算机中，激光导向系统测量得到的盾构机的位置姿态数据实际上正是与生成的这些拟合点的坐标进行比对，从而确定出盾构机姿态偏差量。

如图9-19所示，激光导向系统测量得到刀盘中心O点的坐标为（xO，yO），距离设计轴线最近的两个拟合点分别为n（xn，yn），n+1（xn+1，yn+1）。n与n+1连线的方程为：

其中，。

则O点到n与n+1连线的距离为：

图9-19　刀盘中心水平偏差示意

为保证纠偏过程中平稳且便于调节，盾构机的纠偏曲线需要满足以下约束条件：

①纠偏曲线起点为刀盘中心O点，终点必须回到隧道设计轴线上的一点。

②纠偏曲线连续、光滑。

③纠偏曲线起点位置的斜率与盾构机当前轴线斜率一致，终点的斜率与隧道设计轴线上该点处的斜率一致。

④纠偏曲线的曲率半径不小于允许的最小纠偏半径Rmin。

满足以上条件的纠偏曲线有三次抛物线、辐射螺旋线，此处选用三次抛物线作为纠偏曲线，则纠偏曲线方程为：

纠偏曲线起点为（xO，yO），终点为（xi，yi），根据约束条件1可得：

纠偏曲线方程的一阶、二阶导数分别为：

设盾尾中心坐标为（xO3,yΟ3），纠偏曲线终点的后一个拟合点为（xi+1，yi+1），根据约束条件2、3可得：(www.daowen.com)

根据约束条件4可得：

式中　ρ——纠偏曲线曲率半径（m）；

Rmin——允许的最小纠偏半径（m）。

纠偏曲线优化目标为纠偏曲线最短，也可以表达为起点与终点的连线最短：

起点坐标（xO，yO）、盾尾中心坐标（xO3, yO3）可通过激光导向系统进行测量获得，为优化前的已知条件，纠偏曲线方程中的a、b、c、d为待定系数，而终点坐标、终点处的斜率均未知，无法求取待定系数。此处设计了优化过程：

①计算dO、盾构机轴线斜率kO、离刀盘中心最近的拟合点n处隧道轴线斜率kn。

②判断dO是否大于允许的距离|dO|，kO与kn偏差是否大于允许值ε，以此判断是否需要纠偏。

③以距离刀盘中心最近的一个拟合点n作为终点。

④计算纠偏曲线方程的四个待定系数a、b、c、d。

⑤判断纠偏曲线的最小曲率半径是否小于Rmin。

⑥如果最小曲率半径小于Rmin，则以第n+1个拟合点作为终点，重复进行②、③步骤。

⑦如果最小曲率半径大于Rmin，则该点为满足要求的终点。

优化流程图如图9-20所示。

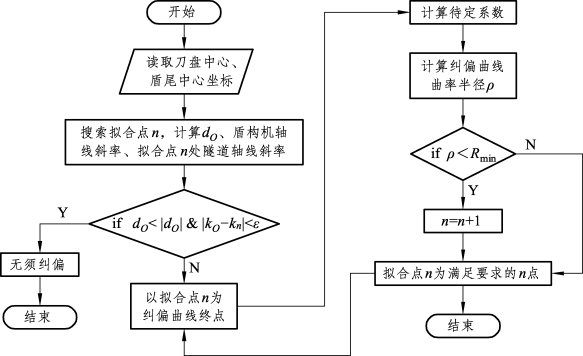
图9-20　水平方向纠偏曲线优化的流程