1）多目标优化方法的算法简介

本节中多目标优化方法采用粒子群优化（PSΟ）算法，粒子群优化（PSΟ）算法是一种模拟社会行为、基于群体智能的进化技术，具有独特的搜索机理、出色的收敛性能等优点。本节采用多目标粒子群优化算法（MΟPSΟ）对边滚刀的布置进行优化。该算法的原理是假设在d维搜索空间中建立粒子种群，第i个粒子具有初始位置和初始速度，每一次迭代计算之后，粒子通过个体极值pbest和全局最优解gbest来不断地更新自己。粒子主要是根据下面的控制参数方程来进行位置和速度的更新：

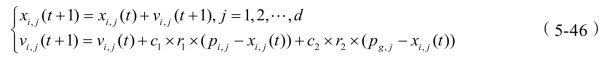
式中　c1、c2——学习因子；

r1、r2——0到1之间均匀分布的随机数。

整个粒子种群利用控制参数方程不断地通过迭代计算更新位置和速度以寻找最优解，因此粒子种群的粒子数量、最大速度和学习因子等是控制算法速度和准确性的关键参数，需要进行合理的选择。

应用粒子群算法解决多个约束条件的多目标优化问题时，可以通过构造相应的惩罚函数，将问题转化为非约束优化目标，由惩罚函数构造的广义目标函数如下式所示：

式中f(x)是多目标优化的原始目标函数，h(k)H(x)是惩罚项。其中h(k)为惩罚函数的惩罚系数，一般初始的为多级分配惩罚函数，可用下式定义：

式中　m——约束条件的个数；

σ(qi(x))——多级分配函数；

q i(x)——约束违反度函数；

λ(qi(x))——惩罚函数的级数。

σ(qi(x))、q i(x)、λ(qi(x))均由约束条件进行控制，它们的作用是通过定义多级分配函数来表达惩罚函数与约束条件之间的关系，根据约束违反度函数值的大小分为不同的等级，通过分级达到优化目标的目的。多级分配函数定义如下：当qi(x)＜1时，级数λ(q i(x))=1；当qi(x)≥1时，级数λ(qi(x))=2；当qi(x)＜0.001时，σ(qi(x))=10；当0.001＜qi(x)＜　0.1时，σ(qi(x))=20；当0.1＜qi(x)＜1时，σ(q i(x))=　100；当qi(x)≥1时，σ(qi(x))=300。

多目标优化的目的是使得每一个子目标都在原有的基础上得到优化，消除短板的存在，所以有些多目标优化算法的结果并不唯一。例如遗传算法有可能会得到几组解，然后再人为从中选择，这无疑使得优化的过程变得复杂了，利用粒子群算法可以通过理想点法简化选择某一个解的过程，计算得到的结果即是最优结果。其中总优化目标可表示为：

理想点法是首先将总优化目标中的每一个分目标函数分别在所有约束条件下优化得到各自的最优值，然后借助最小二乘法的思想，将多目标优化问题转化为求单目标函数（评价函数）的极值。构造的评价函数可表示为：

式中　wi——各子目标权重系数，和为1；

——第i个子目标在所有约束条件下的最优值。(www.daowen.com)

因此，多目标粒子群优化算法的步骤是：

①在约束条件下，分别求得各目标函数的最优值。

②利用多级罚函数粒子群算法求总体评价函数的最优值。

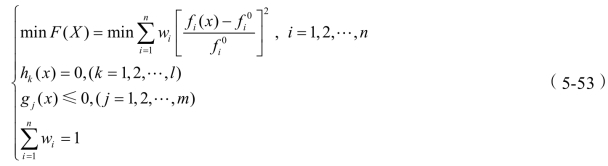
③求得评价函数的最优值，得到优化结果。

2）优化结果与分析

以本节所介绍的成都地铁盾构机的刀盘为例，共12把边滚刀，均为18英寸宽刃滚刀，刃宽20 mm，刀尖圆弧过渡角5°，刀刃角20°，刀圈半径228.5 mm，滚刀质量195 kg，刀尖压力分布系数-0.2，滚刀与岩石接触角0.04 rad。刀盘转速3 r/min（0.314 rad/s），贯入度4 mm。岩石抗压强度145 MPa，抗拉强度4.6 MPa，岩石破碎角1.12 rad。安装后刀盘质心位置误差许用值δxe取50 mm，δye取50 mm。

先对径向不平衡力和倾覆力矩分别进行约束优化，考虑到二者对于刀盘的影响和破坏都是非常严重的，所以认为其权重系数相同，即w1=w2=0.5。利用matlab编程计算，最后得到最优总体评价函数值F0(X)=0.54，如图5-28所示，求解后的结果如表5-18所示。

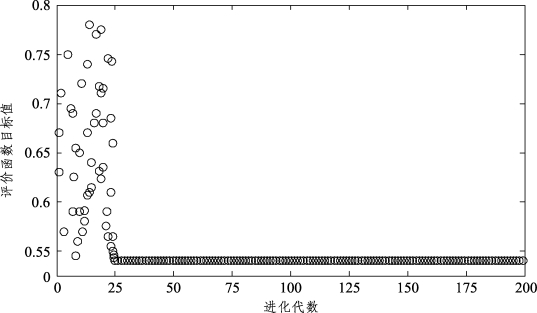
图5-28　多目标评价函数迭代曲线

表5-18　优化前后目标函数值对比

从优化结果可以看到，各项指标都有所优化，径向不平衡力减小了15.31%，倾覆力矩减小了19.39%。不过优化后的径向不平衡力和倾覆力矩仍然较大，这是由于优化过程没有考虑正面滚刀和刮刀的影响，仅基于第4章安装倾角的优化结果对边滚刀的极径进行了优化，优化后的刀盘刀具布置如图5-29所示，图中标黑处为边滚刀位置。统计12把边滚刀优化前后的安装倾角、极径以及极角如表5-19所示。

图5-29　滚刀布置示意

表5-19　优化前后刀具布置参数

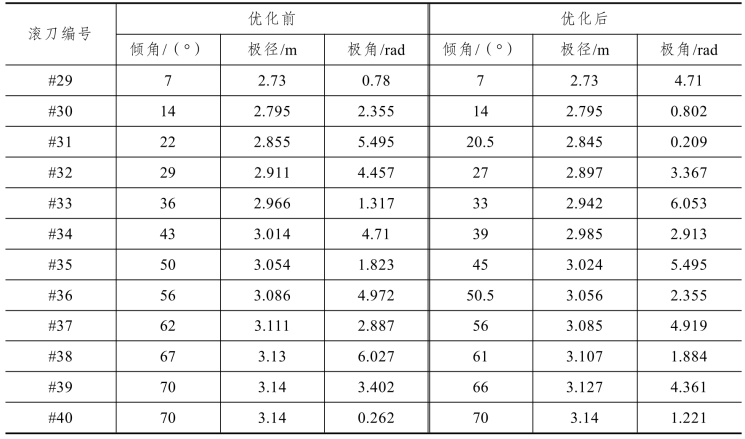
从刀具布置图中可以看到，边滚刀的安装位置满足布置域要求，且互不干涉，最大安装极径与原数据相同，满足隧洞直径的开挖要求，因此综合来看，优化的结果较为可信和满意。