从单因素分析的结果可以看到，刀圈刃宽、刃角、安装倾角以及刀盘圆弧过渡半径都是对破岩效率有影响的。而当它们都为可变量时，对破岩效率的影响就有可能会变得非常复杂了，各因素之间可能存在相互制约，哪个因素对于效率的影响程度更大也未可知，所以研究多因素同时作用是非常有必要的。正交试验是一种适用于解决多因素、多指标、多水平问题的试验方案，主要利用正交表的设计来挑选部分有代表性的水平组合进行试验，摸清各因素对试验指标的影响情况，确定主次关系，找出最优组合水平。

1）正交试验及其结果分析

正交试验的基本步骤有：

①确定试验指标，即明确要解决的问题，确定考核标准。

②确定因素与水平，制定试验因素水平表。

③确定正交表。

④处理数据及结果分析。

基于表5-7单因素分析的参数，本试验共设置4个因素，即刀圈刃宽、刃角、安装倾角和刀盘圆弧半径，每个因素设置5个水平，仿真得到的三向力和破岩体积是为了计算破岩比能耗，所以仅选取破岩比能耗作为试验指标。根据正交表的设计原则，应选取L25（56）的前四列作为本试验安排的正交表，“L”表示正交表，“25”表示要进行25次试验，“5”表示每个因素有5个水平，“6”表示该正交表最多可进行6个因素的试验。由于因素数量不满足，正交表中有空白列可作为误差列以衡量试验的可靠性，将空白列隐去，得到如表5-12所示的试验水平表。

表5-12　L25（56）试验水平

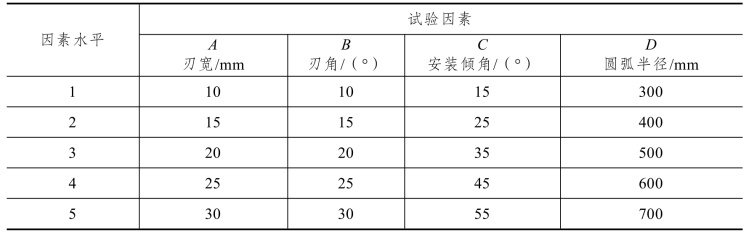
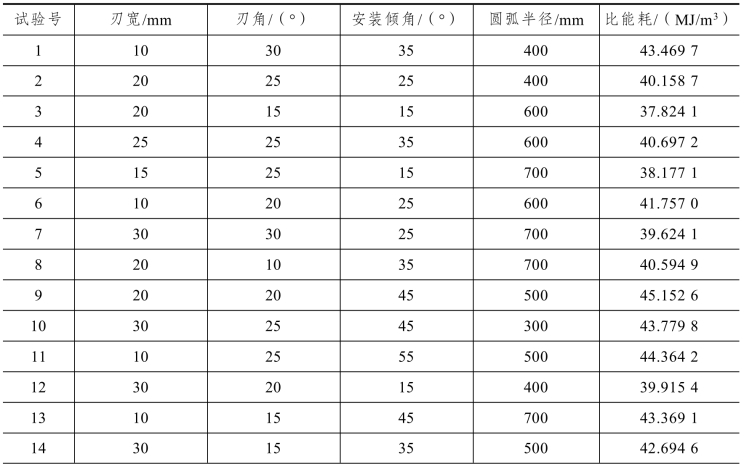
运用SPSS Statistics软件可以生成正交数据表，然后依据每一次试验的参数修改仿真模型进行模拟，将仿真的结果代入已编写的matlab程序计算破岩比能耗，如表5-13所示。

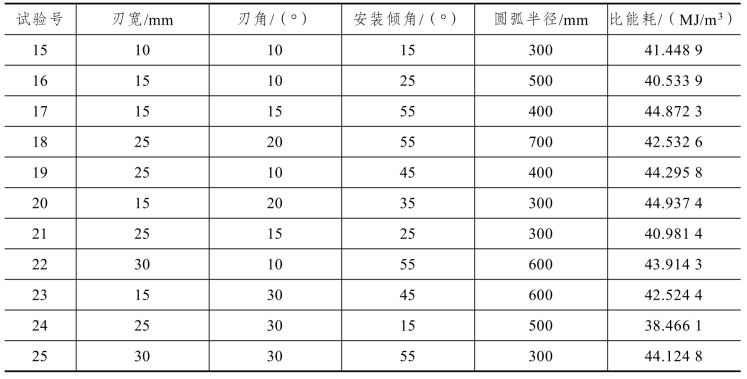
表5-13　正交试验参数及仿真结果统计

续表

在统计学中，显著性检验是统计分析过程非常重要的步骤，它主要是判断某因素对指标的影响程度。在没有进行显著性检验之前，即使已经通过试验得知某因素对指标变化的影响趋势，但显著性检验后发现该因素并不显著，对其研究则毫无意义，甚至影响趋势只是试验过程的误差造成的。只有找到显著影响因素进行完善和改进才能促进指标的优化。

基于表5-13的数据，多因素方差分析法的计算结果如表5-14所示。

表5-14　方差分析计算结果

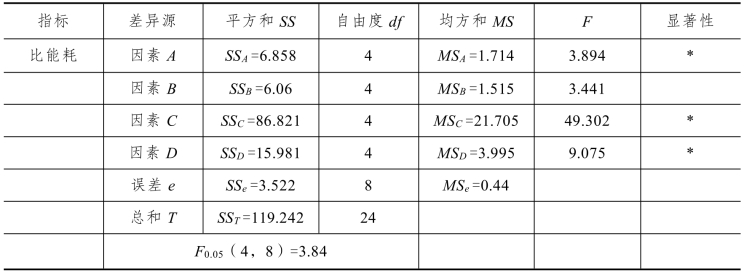
表中各数据的计算过程如下，其中总偏差平方和SST以及自由度dfT为：

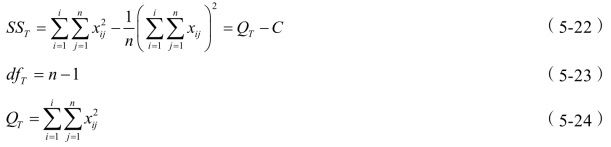
式中　i——因素数量，此处为4；

n——试验次数，此处为25；

QT——各数据平方之和；

C——矫正数；

T——所有试验数据的和。

各因素的偏差平方和SSi以及自由度dfi为（i=A，B，C，D）：

式中　t——因素水平数，此处为5。

误差的平方和SSe为：

误差的自由度dfe为：

各因素与误差的平均偏差平方和MS为（m=A，B，C，D，e）：(www.daowen.com)

各因素的F统计量为（以A因素为例）：

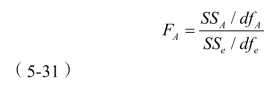
由表5-14的计算结果可知：

①在0.05水平的置信区间内，刀圈刃宽、安装倾角、刀盘圆弧过渡半径的F值均大于3.84，所以这三者是显著的。其中安装倾角的F值远远大于另外三个因素，对破岩效率的影响是最大的，在进行边滚刀的优化布置时应该着重考虑该因素的影响。

②刃宽及刃角对破岩效率的影响较小，为了提高边滚刀的荷载及使用寿命，可以适当选用刃宽和刃角较大的滚刀刀圈。

2）边滚刀安装倾角的优化

正交试验的结果显示安装倾角是对边滚刀破岩效率影响程度最显著的因素，安装倾角越大的边滚刀，破岩力和滚动力相比正面滚刀来说都处于较低水平，破岩能力有限，而单位时间内其破岩轨迹却比正面滚刀要长，因此磨损速度较快。为了有效降低边滚刀的磨损，通常有以下几种处理方式：

①在相同的倾角上布置两把或多把滚刀，多把滚刀共同分担旋转一周的破岩量，以达到减小磨损的目的。

②增大刀盘圆弧过渡半径，减小最边缘滚刀的倾角，改善受力情况。

③减小相邻边滚刀之间的倾角差，以减小刀间距，实现协同破岩，降低滚刀受到的岩石的反作用力。

采用数值模拟的方式对相邻两滚刀的破岩过程进行多组仿真，可以得到低破岩比能耗下的安装倾角，这是一种非常高效的滚刀布置优化方式。

以本节所介绍的成都地铁某盾构刀盘为例，12把边滚刀与前刀的倾角差如表5-15所示，前7把滚刀的倾角差都在7°以上，并没有随着倾角的增大而缩小倾角差。而38、39、40三把刀之间的倾角差突然减小，其中39、40两把刀位于同一破岩轨迹上，因此从倾角差的分布来看，各个滚刀的破岩量和受力很可能是不均匀的。例如33、34、35等几把刀之间倾角差仍为7°显然是不合理的，因为这样不但会造成能量损耗并加剧其自身的磨损速度，还会影响相邻滚刀的承载状态，引起异常磨损，从而产生“链式反应”，导致全盘滚刀损坏或卡机等更加恶劣的结果，所以有必要利用减小相邻滚刀倾角差的方式对安装倾角进行优化布置。

表5-15　12把边滚刀倾角差

第一把边滚刀也称为过渡边滚刀，其安装倾角的大小是非常重要的，一般来说后面布置的滚刀与前刀的倾角差是在第一把边滚刀的倾角的基础上依次递减的。所以第一把边滚刀的倾角不能过大或过小，过小会使得后面布置的滚刀很密，造成资源的浪费，过大则无法实现协同破岩，增加了滚刀的负荷。本节利用前面介绍的创建破岩模型的方法建立第一把边滚刀最优倾角的仿真模型。

模型中共设置两把滚刀，分别为最边缘的正面滚刀以及第一把边滚刀，两把刀均进行刚体约束，正刀的质心参考点与回转中心的距离为2 660 mm，与边刀的质心参考点在刀盘半径方向上的间距为70 mm，两把刀均与岩体设置面与面接触，分别建立Hinge铰接约束控制滚刀的公转和自转，设置相应的边界条件，仿真过程中两把刀以先后顺序切削岩体，所建立的仿真模型如图5-23所示。

图5-23　双滚刀破岩模型示意

为了寻找第一把边滚刀破岩比能耗最低时的安装倾角，需要不断地调整边滚刀的倾角进行仿真，然后利用可视化结果观察岩体被切削的效果，其中边刀的安装倾角分别为5°、6°、7°、8°时的仿真结果如图5-24所示。导出破岩量和两把滚刀的破岩力等数据计算，得到的比能耗结果如图5-25所示。安装倾角为7°时，两把滚刀滚压轨迹之间的岩石单元基本都被切削删除，说明在该倾角下滚刀为协同破岩模式，破岩效果较好。倾角为5°与6°时两滚刀间的岩石单元同样基本都被切削删除，切削槽的宽度依次递减，说明倾角为5°与6°时滚刀为过渡破岩模式，刀间距较小。倾角为8°时可以看到两滚刀间有较为明显的岩脊，有较多的岩石单元没有被切削删除，切削槽之间的应力较小，说明该倾角下两滚刀刀间距较大。从比能耗上也可以看到倾角从5°到7°比能耗是在下降的，在倾角为8°时比能耗突然增大，所以倾角7°是该模型边刀与正刀最佳刀间距的临界倾角，该结果与本节刀盘实例采用的首把边滚刀的倾角是相同的，接下来还需要对剩下的边滚刀的倾角进行优化。

图5-24　倾角5°、6°、7°、8°仿真结果

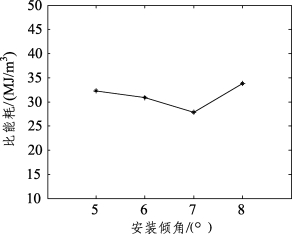
图5-25　比能耗变化趋势

在得到首把边刀最优倾角的情况下，可以采用相同的方法依次得到后面每一把滚刀的最优倾角，但是这样的仿真工作量非常大，每一把滚刀要得到最优倾角需要进行数次破岩仿真，且每次仿真时倾角参数值难以界定。一般来说，由于随着安装倾角的增大，边滚刀与前刀的倾角差是逐级递减的，由于首把边刀最优临界倾角为7°，最后一把边滚刀倾角70°，可以以等差递减方式布置后面所有滚刀的倾角，但为了制造和安装的便利，将倾角差以小数点0.5和1.0取近似值，如表5-16所示。

表5-16　边滚刀倾角布置示意

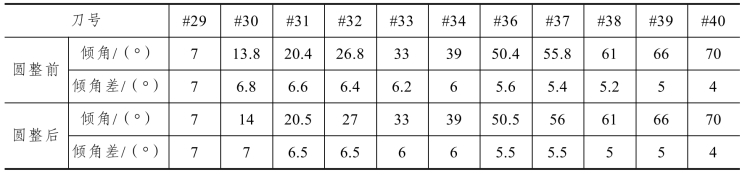
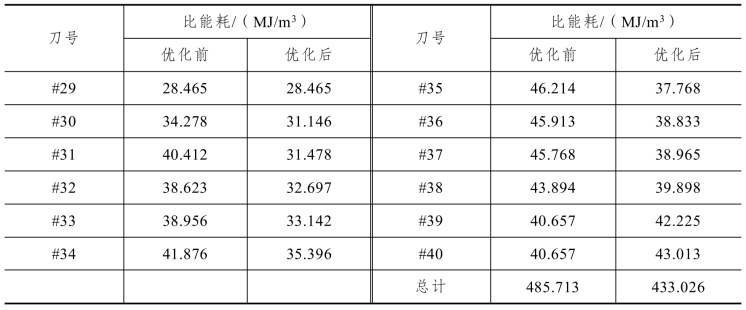
以表5-16中圆整后的安装倾角数据进行两两滚刀破岩的仿真，导出每一把滚刀的垂直力与滚动力和破岩量计算破岩比能耗，再与表5-15中原刀盘安装倾角两两滚刀破岩仿真得到的比能耗结果进行对比，统计结果如表5-17所示。由于采用的是双刀模型，每一把滚刀的破岩比能耗结果都是经过与前刀后刀两次仿真求平均值得到的。将表中数据绘制成比能耗随滚刀编号的变化趋势图，可以看到优化前滚刀比能耗的变化趋势波动剧烈。由于前面7把滚刀的倾角差均等于或大于7°，其整体比能耗高于优化后的结果，而最后两把滚刀因为布置在同一破岩轨迹上，所以比能耗较小，优化后的滚刀比能耗变化趋势整体比较平缓。从比能耗的变化上可以推断优化后相邻滚刀的破岩效果较好，磨损程度相近，使用寿命更长。

表5-17　优化前后滚刀比能耗结果统计

因此，在实际工程中设计刀盘的安装倾角时，可以先确定首把边滚刀的最优倾角，然后依据倾角差等差递减的方式布置后面的滚刀，以本优化结果为例，优化后所有边滚刀的破岩比能耗相比优化前减少了12.17%，优化结果较好，在一定程度上可以提高掘进效率，同时延长了刀具的使用寿命，减少了因为边滚刀损坏而开舱换刀的概率（图5-26）。

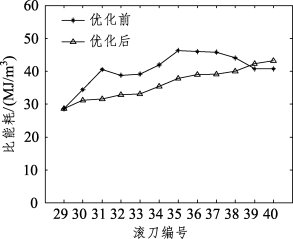
图5-26　优化前后比能耗随滚刀编号变化示意