1）切削现象分析

滚刀在设定好的边界条件作用下回转切削岩体，当滚刀接触岩体单元时给其施加应力作用，单元所承受的应力超过其弹性应变的极限荷载时，开始发生塑性应变。紧接着进入刚度衰减过程，滚刀进一步滚压，这部分单元处于损伤失效状态，由于开启了单元删除功能所以失效的单元均被删除。截取仿真1 s、1.5 s、2 s、2.5 s时的应力云图（图5-16），调整云图应力梯度范围后，可以看到滚刀滚压过的岩体出现了一条切槽，滚压过的位置有残余应力存在，滚刀两侧应力值大小明显不同，这与边滚刀的破岩机理是一致的，边滚刀破岩时由于刀盘正向推力的作用，会使得滚刀两侧的侧向力大小不同。

图5-16　1 s、1.5 s、2 s、2.5 s时滚刀切削轨迹的应力云图

创建滚刀刚体约束参考点的ΟDB场变量可以输出其三向力随时间变化的结果，或者导出参考点应力随时间变化的X，Y值在matlab中绘图，滚刀垂直力、滚动力和侧向力的时间历程变化如图5-17所示。

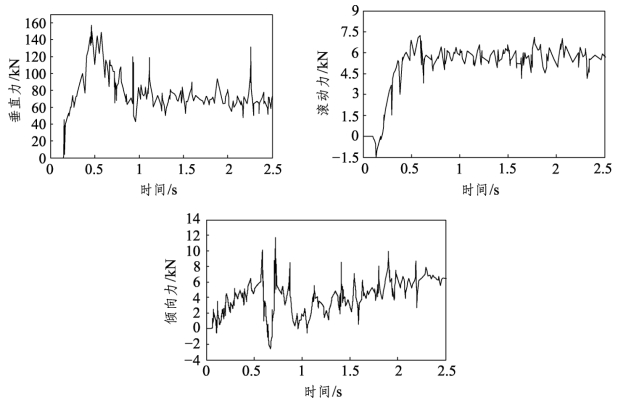
图5-17　倾角7°边滚刀破岩三向力随时间变化曲线

从该滚刀受力随时间的变化曲线中可以看到，在第一个分析步0.5 s的时间内，滚刀匀速向下滚压岩石，所受的应力随着下压深度增加而不断增大，垂直力和滚动力的变化尤其明显，因此当滚刀的贯入度越大时，刀盘需要提供的推力和扭矩也越大。0.5 s后滚刀开始做回转运动，由于此时滚刀的贯入度为定值，垂直力、滚动力和侧向力的变化范围较为稳定一些，但仍然不断上下波动。这是因为滚刀向前与新的岩石面接触，岩石单元处于弹塑性阶段，滚刀所受的反力剧烈增大，增大到一定极限时，超过岩石单元的极限应力，岩石单元开始损伤失效，完全失效的单元被删除后，由于出现破空面，滚刀所受的反力瞬间减小，当再次与新的岩石面接触时压力又开始增大，从而不断地重复这一过程。这样的循环往复称为阶跃式破碎过程，与滚刀实际的破岩现象是一致的。

2）切削力及破岩比能耗分析

利用与边滚刀仿真相同的方法建立其他倾角的边滚刀的仿真模型，得到它们的切削力时间历程曲线，分析其切削力变化规律。12把边滚刀在刀盘上的布置参数如表5-4所示。

表5-4　刀盘实例12把边滚刀布置参数

(www.daowen.com)

选择其中#30边滚刀、#31边滚刀、#32边滚刀分别建立仿真模型，同样取贯入度为4 mm，刀盘转速3 r/min，则它们的自转角速度分别为3.841 rad/s、3.923 rad/s、4.001 rad/s。

仿真结束后导出三向力随时间变化的值，因为第一个分析步是滚刀侵入岩石的过程，不属于稳定破岩阶段，所以剔除时长0.5 s之前的数据，对0.5～2.5 s时间内的应力求平均值。将边滚刀受力分析的理论方法代入仿真的参数，计算得到其三向力的理论值，二者的统计结果如表5-5所示，与滚刀编号之间的关系如图5-18所示。

表5-5　#29、#30、#31、#32边滚刀仿真结果

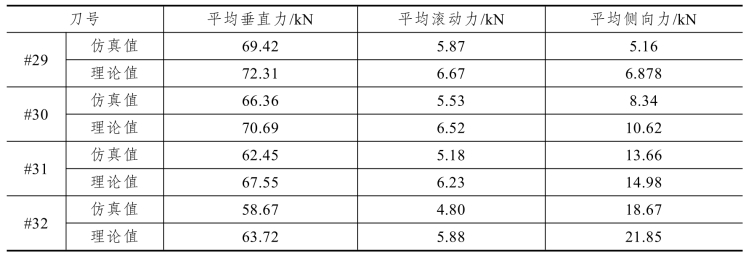
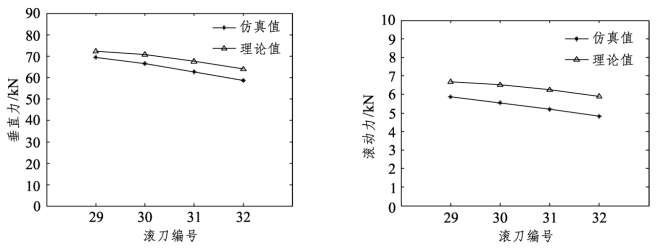
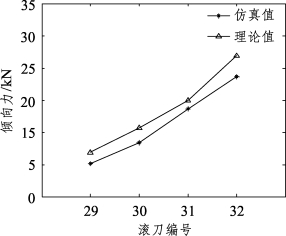
图5-18　不同倾角滚刀三向力变化趋势

从图中可以看到三向力的仿真结果和理论计算的变化趋势是一致的，仿真值比理论值要小一些，可能是因为在模型中将滚刀刀圈看作刚体，而实际的滚刀刀圈是线弹性体，相比实际破岩时的受力情况简单，不过从力的变化趋势看，仿真结果是较为可信的。利用边滚刀受力分析公式代入这4把滚刀的三向力仿真结果后计算它们的破岩比能耗，结果如表5-6所示。表中的破岩体积由仿真结束后计算被删除单元的数量乘以单个单元的体积得到。

表5-6　破岩比能耗计算结果

越靠近刀盘边缘的滚刀破岩比能耗越大，这样的结果与工程实际经验是符合的。由于边滚刀安装倾角增大，其垂直力和滚动力减小，侧向力减小，将直接影响到滚刀的贯入能力和破岩能力。而且在实际施工过程中，越靠近边缘的边滚刀因为破岩轨迹长所以需要破碎更多的岩石，因此如果边滚刀配置不合理的话，极易发生滚刀磨损失效，从而开始磨损刀盘边缘或者在刀盘推力较小的时候发生掘不动岩石的情况，将会严重影响到设备的使用寿命和施工进度。