滚刀在仿真时进行了刚体约束，其网格划分结果对于仿真结果没有太大影响，为了使网格划分均匀，采用四结点线性四面体单元（C3D4）进行划分，选取Explicit单元库，单元数为7 061。岩体釆用八结点线性六面体单元，选择减缩积分、沙漏控制属性，设置单元删除选项。为了保证仿真计算结果的准确性，同时提高运算速度，将岩体进行拆分，分别对各部分进行网格划分，边滚刀破岩的圆弧过渡区域网格尺寸为0.01，其余部分网格尺寸为0.02，单元总数为191 260。网格划分结果如图5-13所示。

Intprop设置滚刀切削的法向行为和切向行为参数，法向行为选择“硬接触”，切向行为选择“罚接触”，摩擦因数设为0.3。

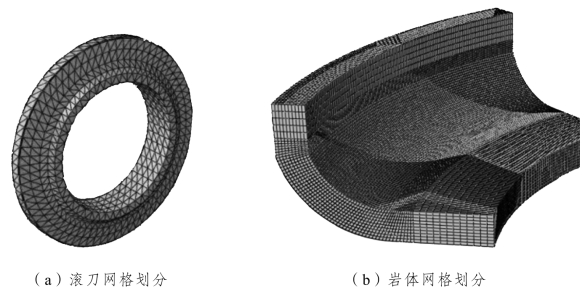
图5-13　网格划分示意

利用Constraints模块将滚刀进行刚体约束，选择滚刀上某点作为滚刀刚体的参考点，并设置在分析过程中将点调整到质心。由于滚刀的运动是绕其自身轴线的自转与绕刀盘中心轴线公转的合运动，在滚刀质心参考点处设置一个局部坐标系，用来控制仿真过程中滚刀的自转，还需创建一个约束用来控制滚刀的公转运动。从相对运动来看，滚刀与刀盘中心轴线之间只有一个旋转自由度，利用Connector模块的Hinge铰链约束可以表示这种运动关系，如图5-14所示是ABAQUS软件提供的Hinge约束原理示意。

图5-14　Hinge铰链约束示意

在刀盘中心轴线处创建一个参考点作为运动控制点，选择已有的滚刀中心的参考点作为铰接点，用Hinge功能连接运动控制点和铰接点，则两点之间将只有绕其连接线的转动自由度，其余两个转动自由度和三个平动自由度都是被限制的。在运动控制点创建一个局部坐标系，当设定运动控制点绕坐标系某轴转动时，铰接点将跟随运动控制点做转动运动，即实现让滚刀围绕刀盘中心轴线公转。如图5-15所示为单滚刀回转破岩模型，如果在有多把滚刀顺次破岩的情况下，需要建立多个Hinge约束以及多个局部坐标系，分别控制每把滚刀的运动形式。

由于在仿真过程中只有滚刀在运动，岩体是不改变位置的，因此在初始分析步Initial中设定岩体的底面为全自由度约束的边界条件。在自行创建的第一个分析步中设置滚刀的自转同时匀速下压的边界条件，该分析步结束时滚刀侵入岩石的深度为指定的贯入度，第二个分析步设置滚刀自转速度和公转速度的边界条件，二者之间的关系如下式：(www.daowen.com)

图5-15　滚刀回转运动控制模型

式中Rv——刀盘的转速，即滚刀公转速度（r/min）；

vr——滚刀的转速（r/min）。

其中安装极径ρ和滚刀半径r都是已知的，每把边滚刀的极径不同，对不同倾角的边滚刀做破岩仿真时，需要重新进行计算并设定边界条件。本模型假设刀盘转速为3 r/min，由于边滚刀#29破岩轨迹与刀盘中心间距为2 730 mm，则设置滚刀公转角速度为0.314 rad/s，滚刀自转角速度为3.751 rad/s，第一个分析步时长0.5 s，第二个分析步时长2 s。为了模拟边滚刀在刀盘推力作用下的破岩特性，在第二个分析步中施加垂直向下的推力荷载，用CSM模型计算推力大小。

在边界条件设置完成后，可以修改分析步中的质量因子，经过对比发现修改质量因子几乎不会对仿真结果产生影响，但会明显缩短仿真时间，可取质量因子为1 000。