通常认为盘形滚刀侵入岩石时的受力可以分解为如图5-3所示三个方向：垂直于掌子面的垂直力Fn，由推进系统反向推进刀盘得到；与滚刀刀圈外圆相切的滚动力Fr，由刀盘驱动系统提供的扭矩得到；指向刀盘轴线的侧向力Fs，由离心力和滚刀侵入岩石的侧向剪切力合成得到。对于正面滚刀而言，Fs远小于Fn和Fr，因此可以将其忽略；然而对于边滚刀，因为有安装倾角，其受力情况比较特殊，其侧向力不可忽略。

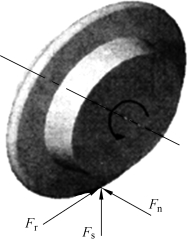
图5-3　滚刀所受三向力示意

关于滚刀切削岩石受力的计算已有较多的学者对此进行过研究，而目前应用较多的是CSM预测模型。该模型由科罗拉多矿业学院（CSM）经过多次对滚刀在不同切入深度、不同滚刀间距、不同滚刀尺寸条件下进行切削试验得到。CSM模型示意图如图5-4所示。

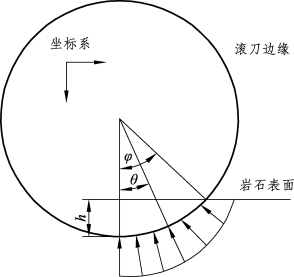
图5-4　滚刀正面CSM受力分析

对于正面滚刀其合力Ft可以由下式表示：

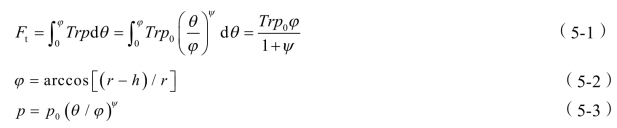
式中　φ——滚刀与岩石接触弧的度数；

T——滚刀刀圈刃宽（mm）；

r——滚刀半径（mm）；

p——岩石破碎区任意一点压力（kPa）；

p0——刀圈下方破碎区压力（kPa）；

θ——刀刃工作点与破岩最深点夹角（°）；

ψ——刀尖压力分布系数；

h——刀尖贯入度（mm）。

其中，刀尖压力分布系数取值范围是-0.2≤ψ≤0.2，当刀圈刃形为楔形时，ψ取0.2，反之，刃宽越大时取值越小，最大情况下取值-0.2。刀圈下方破碎区压力可以用下式表示：

式中　C——常数，恒等于2.12；

S——滚刀间距（mm）；

σc——岩石单轴抗压强度（kPa）；

σt——岩石抗拉强度（kPa），约为抗压强度的1/10～1/30。

联立式（5-1）～式（5-4），可以推导得到滚刀垂直力Fn和滚动力Fr：(www.daowen.com)

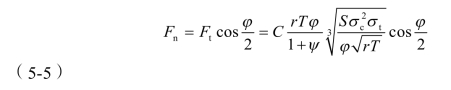
因此滚动力Fr和垂直力Fn之间存在线性关系，当滚刀垂直力大小不变时，随着滚刀与岩石接触弧的度数φ的增大，滚动力相应增大，由此垂直力Fn和滚动力Fr之间的关系又可以用下式表示：

滚刀的侧向力利用下式计算，该式应用空间运动学原理根据滚刀破岩时的运动特性推理得到：

式中　τ——岩石抗剪强度，约为抗压强度的1/8～1/12（kPa）；

ρ——滚刀安装极径（mm）。

上述计算过程是CSM模型对于面板刀破岩的受力计算，而对于边滚刀来说，其对于掌子面的法向推力需要经过一些转换计算得到。边滚刀在刀盘正面及截面的受力示意如图5-5所示，根据刀盘的设计理论，所有滚刀在刀盘推力的作用下受到的隧道轴线方向的反作用力大小相同，目的为平均分担刀盘荷载。对于正面滚刀来说，隧道轴线方向的反作用力与垂直力大小相同；对于边滚刀，由于有安装倾角α存在，所以其垂直力是隧道轴线反作用力在滚刀法平面的分力。

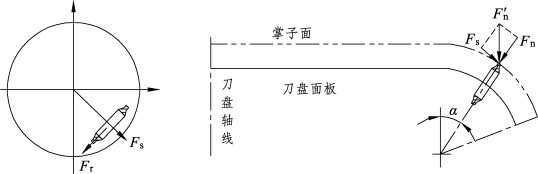
图5-5　刀盘推力和各滚刀法向推力示意

由此可以认为，仍然可以利用CSM模型计算边滚刀垂直力和滚动力，在边滚刀法面方向，其破岩机理和面板刀的破岩机理是一样的。在计算时，边滚刀的垂直力需要在原有垂直力公式的基础上考虑安装倾角的影响，由于本书仅对边滚刀进行研究，下文中Fn、Fr、Fs分别表示边滚刀的垂直力、滚动力和侧向力。其中垂直力可以用下式表示：

边滚刀滚动力仍然可以用计算，随着安装倾角的增大，边滚刀法面方向的推力逐渐减小，同样的其滚动力也随之逐渐减小。

侧向力的计算视盾构工况而定，滚刀在刀盘推力作用下已贯入掌子面中做纯滚动时，仍然可用式（5-8）计算，但考虑到边滚刀变切深的特性，如图5-6所示，某安装倾角的边滚刀其实际贯入度为刀盘贯入度与倾角余弦值的乘积，将计算式改进为：

图5-6　边滚刀变切深特性

在刀盘推力作用下，计算时还需要考虑隧道轴线方向作用力在侧向的分力，可用下式计算：

由式可知，随着安装倾角的增大，边滚刀的侧向力是在不断增大的，因此越靠近刀盘边缘的滚刀，受力情况越恶劣，对刀圈的磨损和轴承受力都有不利影响。