采用包含交叉加强的XFEM的位移模式来表示包含自然裂纹和水力裂纹的裂纹体的位移模式；对于裂尖加强结点，需根据裂尖内是否充满流体，裂尖加强函数采用不同的奇异指数，具体形式为

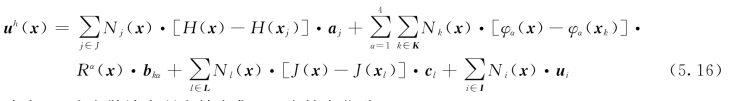
式中：I为离散域内所有结点集，ui为结点位移，Ni（x）为结点形函数；J为裂纹贯穿的单元结点的集合（图5.3中标“□”和“◇”的结点），用广义的Heaviside加强函数H（x）来加强，在裂纹一侧等于1，在裂纹另一侧等于-1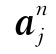，为相应的附加变量；K为K*与其邻近结点（与K*中结点共享单元的结点，图5.3中标“○”的结点）的集合，bkα为相应的附加变量；L为裂纹交叉点所在单元结点的集合[图5.3（b）中标“×”的结点]；R（x）=为裂尖处为了消除混合单元而引入的线增函数。

对于各向同性弹性体，裂尖加强函数φα（x）（α=1，…，4）一般采用下列裂尖分支函数：

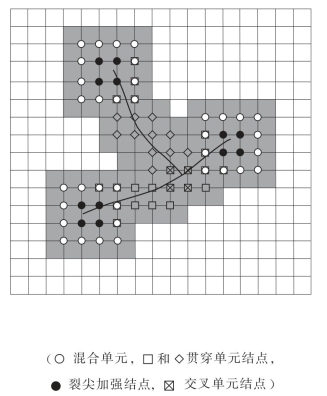
图5.3　加强结点及加强类型

其中，r和θ为裂尖处的局部极坐标；当裂尖没有流体时λ=，当裂尖充满流体时λ=。

裂纹交叉单元的连接加强函数J（x）和形函数Ni在第3章中已给出。为了提高裂纹附近精度，裂纹附近结点形函数Ni同样采用广义形函数，如图5.3中的灰色部分。

根据XFEM位移模式式（5.16），可以计算自然裂纹面的相对位移uc，第2章已给出。水力裂纹宽度w和uc的表达形式相似，即

(www.daowen.com)

式中：d为单元结点参数列阵；T为局部坐标和整体坐标的转换矩阵；d和T的具体表达式详见第3章；Nc为结点的形函数，和裂纹单元的结点加强方式有关。

其中

对于H（x）或Jq（x）函数加强的结点：

对于φα（x）函数加强的结点：

其中，当裂尖没有流体时λ=，当裂尖充满流体时λ=。