无限大板中含有一条倾斜的水力裂纹，裂纹内静水压力为P，水力裂纹和水平最大主应力方向的夹角为β，岩体材料参数和围压值见表4.2。数值分析中，选取150m×150m的正方形区域，裂纹长度为10m，见图4.6（a）。采用120×120个单元的计算网格时，裂纹附近的加强结点和加强类型见图4.6（b）。

表4.2　力学参数

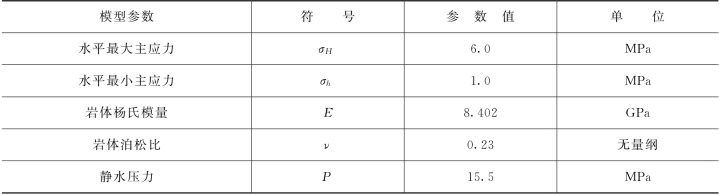
无限大板内单一的倾斜的水力裂纹在静水压力和水平主应力作用下，裂尖Ⅰ型和Ⅱ型应力强度因子的解析表达式为[155]

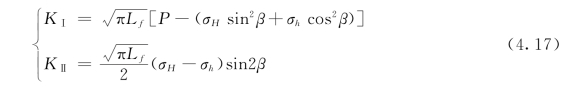
式中：σH、σh分别为水平最大主应力和水平最小主应力；Lf为一半裂纹的长度。

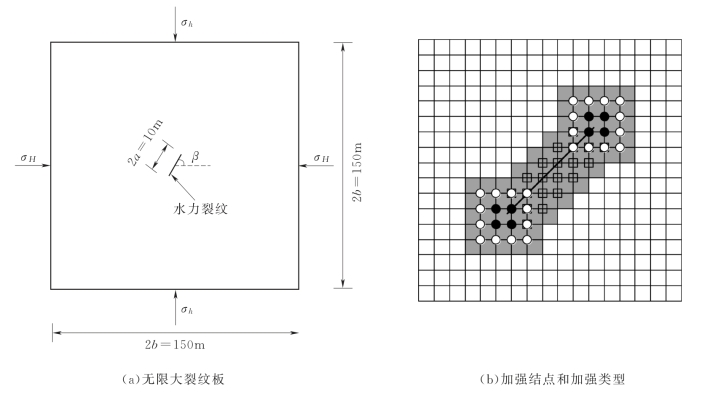
图4.6　无限大板中含有倾斜的水力裂纹

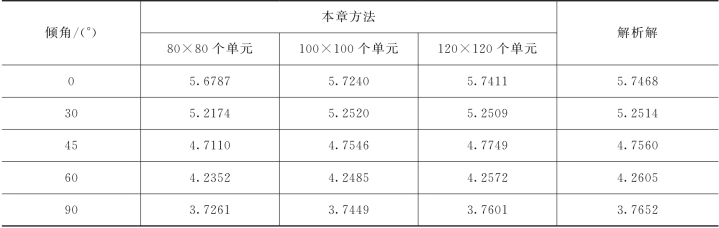
使用三种密度的网格（80×80个单元、100×100个单元、120×120个单元）计算应力强度因子，并与文献[155]中的解析解进行比较，结果比较见表4.3和图4.7。从表4.3和图4.7可得：(www.daowen.com)

（1）应力强度因子的精度随着网格的加密而逐渐接近于精确解，在100×100个单元的网格中得到的值已十分接近精确解，可见在达到一定的网格密度时，细分网格对精度的影响不大；

（2）随着夹角β的增大，Ⅰ型应力强度因子呈现逐渐减小的趋势，这是由于随着β角的增大，水平最大主应力对裂纹面产生的压力效应越大，使得裂纹面上的有效拉应力逐渐减小，也表现为Ⅰ型应力强度因子逐渐减小。

表4.3　不同网格下的应力强度因子　单位：107 Pa/m2

通过上述两个算例分析可以看出，本章的方法能有效地计算水力裂纹的裂尖应力强度因子。

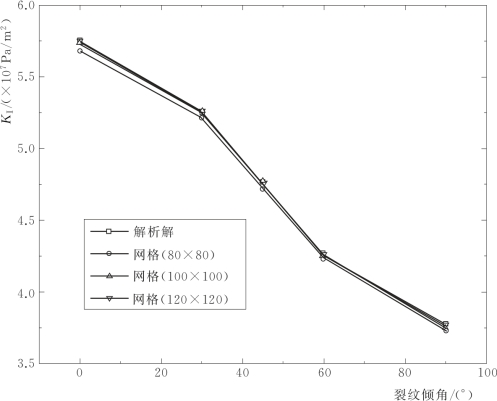
图4.7　不同倾角下的应力强度因子