3.5.3.1　两共线裂纹

含两共线裂纹的板受单向压力作用，如图3.12所示。弹性模量E=10单位，泊松比ν=0.3；裂纹面间的摩擦系数f=0.3；p=1单位。两裂纹与x轴的夹角为45°。计算网格由19×19个四边形单元组成，裂纹附近的网格及加强结点和加强类型见图3.13。为了和已有文献结果相比较，此处只计算Ⅱ型应力强度因子。定义正则化的应力强度因子为：FA是在相同荷载下单裂纹的应力强度因子。

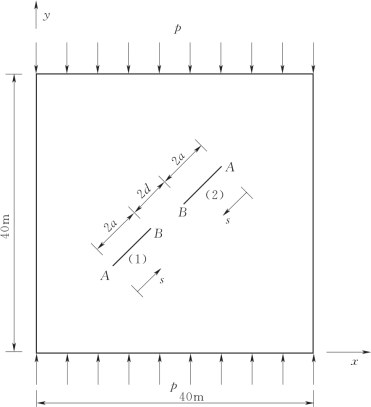
图3.12　受压作用下的两共线裂纹

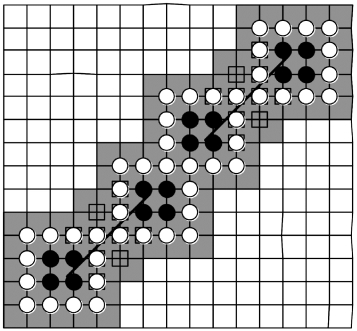
图3.13　两共线裂纹的加强结点和加强类型

表3.4给出了不同d/a的正则化应力强度因子。不同方法获得的不同d/a的正则化应力强度因子见图3.14。根据文献[147]的结论：随着d/a逐渐趋近于1，正则化应力强度因子趋近于1。由图3.14可知，本章方法计算得到的应力强度因子比文献[147]中的精度要高，尤其是在d/a＜0.25时；当d/a比较小时的精度也是很高的；通过和传统XFEM的计算结果相比较，可以看出本章方法能大大改善裂纹附近的精度。

表3.4　不同d/a下两共线裂纹的正则化应力强度因子

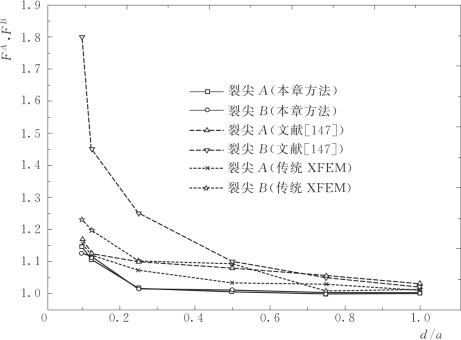
图3.14　两共线裂纹的正则化应力强度因子随d/a的变化

裂纹（1）的两个裂尖坐标为（10m，10m）和（17.5m，17.5m），裂纹（2）的两个裂尖坐标为（22.5m，22.5m）和（30m，30m），此时的裂纹面接触力和接触状态见图3.15。裂纹长度在0～10m之间处于滑移状态，之后的裂纹段处于粘连状态。由于两裂纹与x轴的夹角为45°，故在滑移区域的法向接触力和切向接触力的值的大小基本相等。图3.16为变形图，虚线为变形前图，实线为变形后图（放大10倍）。

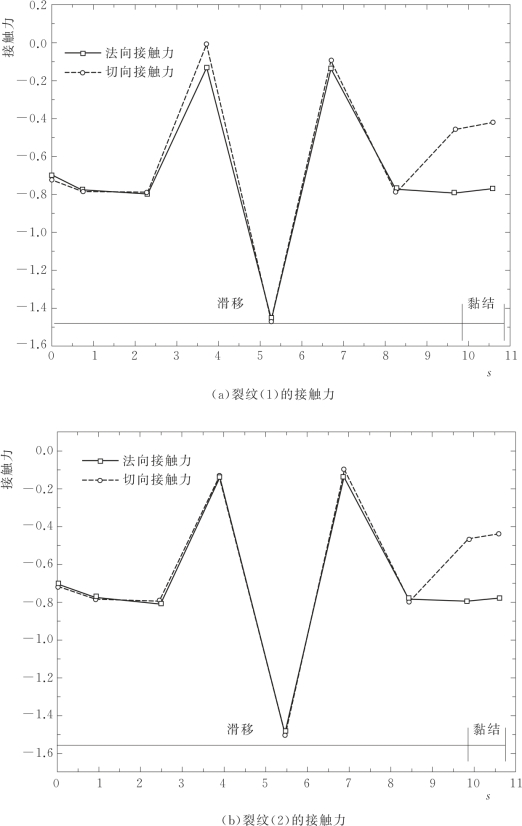
图3.15　两共线裂纹的裂纹面的接触力

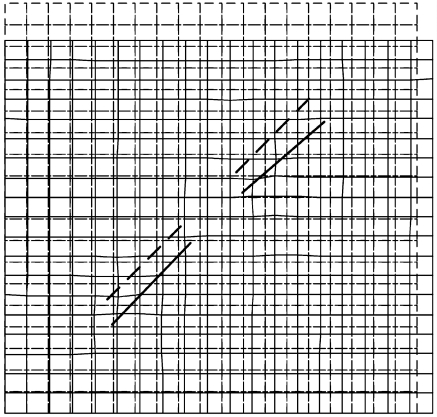
图3.16　两共线裂纹的变形图

3.5.3.2　两平行裂纹(www.daowen.com)

含两平行裂纹的板受单向压力作用，如图3.17所示。弹性模量E=1000单位，泊松比ν=0.3；裂纹面间的摩擦系数f=0.3；p=1单位。两裂纹与x轴的夹角为45°。计算网格由19×19个四边形单元组成，裂纹附近的网格及加强结点和加强类型如图3.18所示。定义正则化的应力强度因子为是在相同荷载下单裂纹的应力强度因子。

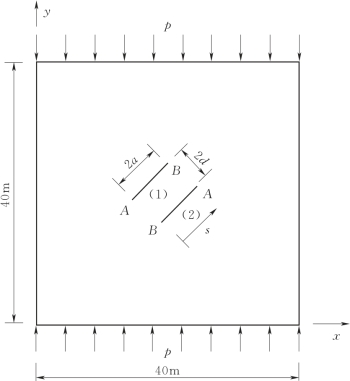
图3.17　受压情况下的两条平行裂纹

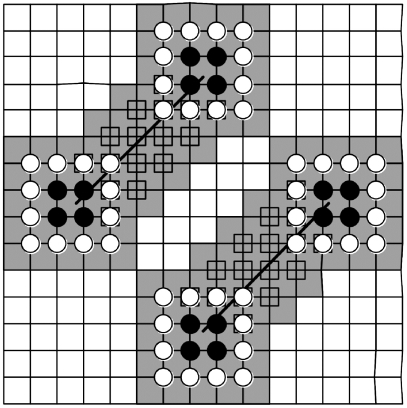
图3.18　两平行裂纹的加强结点和加强类型

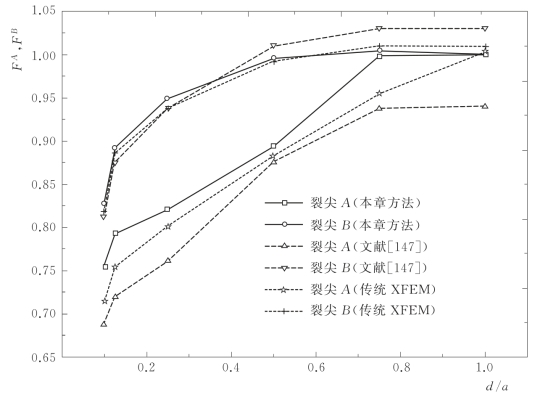
图3.19　两平行裂纹的正则化应力强度因子随d/a的变化

表3.5给出了不同d/a下的正则化应力强度因子。不同方法获得的不同d/a下的正则化应力强度因子见图3.19。根据文献[147]的结论：随着d/a逐渐趋近于1，正则化应力强度因子趋近于1。由图3.19可知，本章方法计算得到的应力强度因子比文献[147]中的精度要高；当d/a比较小时的精度也是很高的；通过和传统的XFEM的结果比较，可以看出用本章方法能明显改善裂纹附近的精度。

表3.5　不同d/a下两平行裂纹的正则化应力强度因子

裂纹（1）的两个裂尖坐标为（10m，20m）和（20m，30m），裂纹（2）的两个裂尖坐标为（20m，10m）和（30m，20m），此时的裂纹面接触力和接触状态见图3.20，整个裂纹处于滑移状态。由于两裂纹与x轴的夹角为45°，所以在整个裂纹段法向接触力和切向接触力的值的大小基本相等。图3.21为变形图，虚线为变形前图，实线为变形后图（放大10倍）。

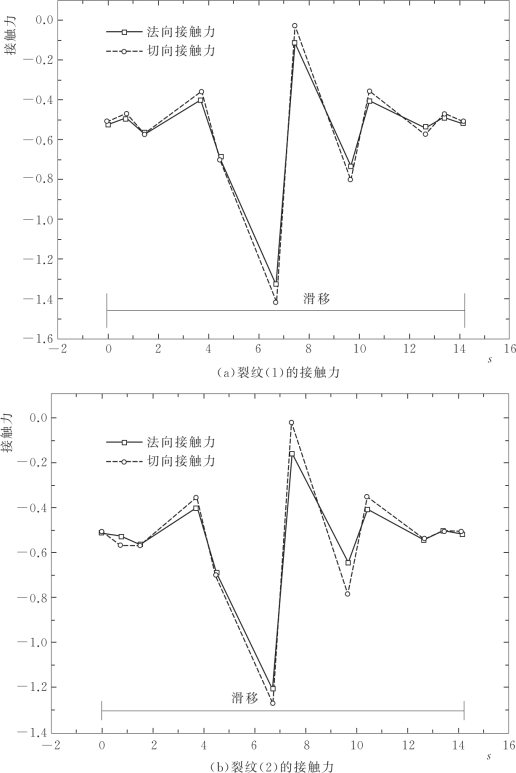
图3.20　两平行裂纹的裂纹面的接触力

图3.21　两平行裂纹的变形图