含两条裂纹的板，底部固定，顶部拉应力p=1单位，如图3.7所示。裂纹（1）的裂尖坐标为（1.2m，8m）和（6m，8m），裂纹（2）的裂尖坐标为（6.6m，6m）和（6.6m，10m）。板的材料参数为：杨氏模量E=10单位，泊松比ν=0.3，临界应力强度因子为KC=1单位；裂纹面间的摩擦系数f=0.3。计算网格由19×39个四边形单元组成，裂纹附近的网格及加强结点和加强类型见图3.8。

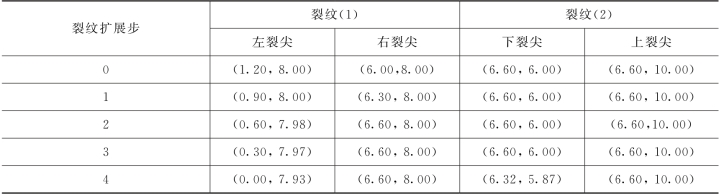
裂纹扩展步长为0.3m，设置的扩展步为4步。根据扩展准则，裂纹的扩展路径如图3.9所示。表3.2列出了扩展中两裂纹的裂尖坐标，可以看出：首先是裂纹（1）的两个裂尖扩展，当裂纹（1）的一个裂尖与裂纹（2）交叉汇合，另一个裂尖扩展至边界后，原来不扩展的裂纹（2）的一个裂尖的应力强度因子超过临界应力强度因子，从而开始扩展。图3.10给出了裂纹扩展后的变形图。

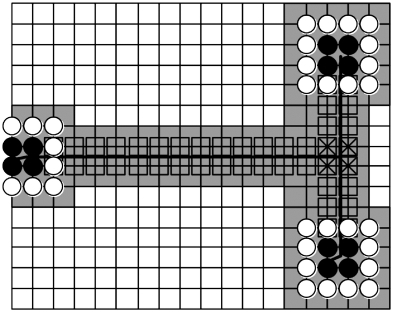
图3.8　加强结点和加强类型

图3.9　裂纹扩展路径

图3.10　变形图(www.daowen.com)

表3.2　裂纹扩展时的裂尖坐标　单位：m

由于板顶部受拉，因此两条裂纹都是开张扩展。为了检验本文裂纹面接触算法的正确性，将图3.7板顶部荷载改为压应力，裂纹（1）绕裂纹（1）的中点[即坐标点（3.6m，8m）]逆时针旋转25°，裂纹（2）绕裂纹（2）中点[即坐标点（6.6m，8m）]逆时针旋转63.4°，其他条件不变。裂纹扩展步长取为0.44m，扩展步为2步。表3.3列出了扩展中两裂纹的裂尖坐标，可以看出：首先是裂纹（1）的两个裂尖扩展，当裂纹（1）的一个裂尖与裂纹（2）交叉汇合，原来不扩展的裂纹（2）的一个裂尖的应力强度因子增大但是不超过临界应力强度因子，裂纹（2）不扩展。裂纹附近的变形图见图3.11，虚线为变形前，实线为变形后。由图3.11可知，裂纹面没出现嵌入现象，由此可见增广型Lagrange乘子法的接触算法的正确性。

表3.3　裂纹扩展时的裂尖坐标　单位：m

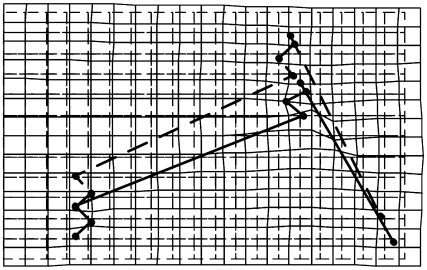
图3.11　受压状态下裂纹附近变形图