多裂纹体的XFEM位移逼近与单裂纹的形式相似，但在裂纹相互交叉的单元需引入交叉加强函数。多裂纹体的XFEM位移模式为

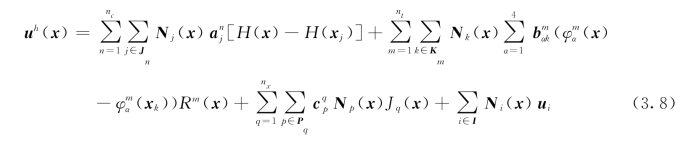
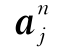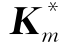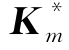式中：I为离散域内所有结点集；ui为结点位移；Ni（x）为结点形函数；nc、nt和nx分别为裂纹数、裂尖数和裂纹交叉点数；Jn为被第n条裂纹贯穿的单元结点的集合（图3.2中标“□”和“◇”的结点），为相应的附加变量；为第m个裂尖所在单元结点的集合（图3.2中标“”的结点），Km为与其邻近结点（与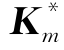中结点共享单元的结点，图3.2中标“○”的结点）的集合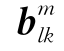，为相应的附加变量；Pq为第q个裂纹交叉点所在单元结点的集合（图3.2中标“”的结点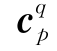），为相应的附加变量；H（x）为广义的Heaviside函数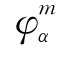；（x）为第m个裂尖的裂尖加强函数；Jq（x）为第q个裂纹交叉点的连接加强函数；Rm（x）为第m个裂尖处的线增函数，该函数的引入是为了消除裂尖加强函数引起的混合单元[116]。

对于裂纹贯穿单元的加强函数H（x），取广义的Heaviside函数。在裂纹的一侧为+1，另一侧取-1，即

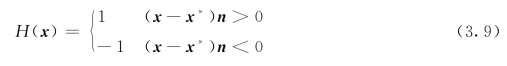
式中：x为考察点，x*为裂纹上距离考察点x最近的点，n为x*点处裂纹的单位外法线矢量。

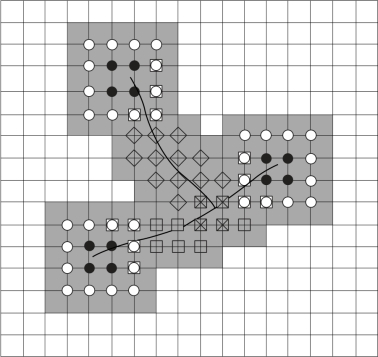
图3.2　多裂纹的加强结点及加强类型

对于各向同性弹性体，裂尖加强函数一般采用下列裂尖分支函数：

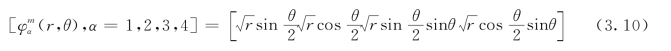
式中：r和θ为裂尖处的局部极坐标。(www.daowen.com)

线增函数Rm（x）为

多裂纹和单裂纹的位移模式的不同在于增加了交叉单元，在裂纹的交叉单元要引入交叉加强，以反映裂纹两侧位移的不连续性，交叉加强函数可用一个连接加强函数Jq（x）[92]：

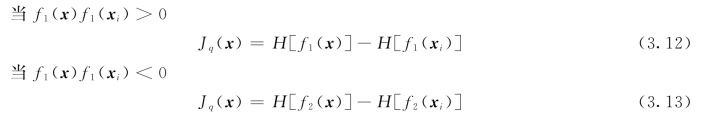
式中：f1（x）和f2（x）分别为关于主裂纹（图3.2中有两个裂尖的裂纹）和次裂纹（图3.2中只有一个裂尖的裂纹）的符号距离函数，表达式为

式中：x为考察点；x*为裂纹面上的一点；n为裂纹面上的单位外法线矢量。

岩体水力裂纹扩展比一般裂纹扩展问题，对裂纹附近精度要求更高。为了提高裂纹附近的精度，将广义有限单元法的广义形函数引入到扩展有限单元法，对裂纹附近结点采用广义形函数，其他结点仍采用常规有限元形函数，这样在稍增加计算量的情况下，能有效地提高裂纹附近的应力状态，以便更好地描述裂纹扩展。考虑计算量和精度的提高，含加强结点单元的结点采用一阶广义形函数，其余结点用传统有限元的形函数，图3.2灰色区域内结点采用一阶广义形函数。一阶广义形函数矩阵为[112]

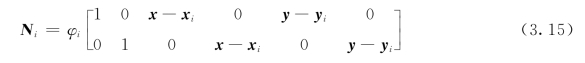
式中：φi为传统有限元形函数。