图2.20为含一贯穿斜裂纹的矩形板，板左端固定，右端受到q=10000Pa的均匀压力。裂纹面摩擦系数f=0.3。板长3m，宽为2m，裂纹面与x轴夹角为β=50°，裂纹与上边界的交点坐标为（1.9m，2m）。假设斜裂纹处于完全接触状态。

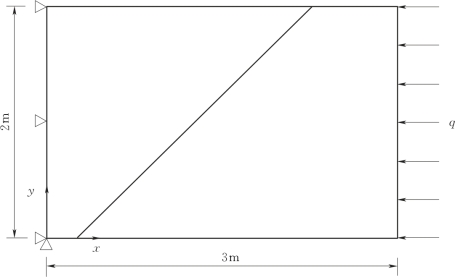
图2.20　完全接触状态下的倾斜裂纹

在完全接触条件下，该问题存在解析解。为了验证本文方法的正确性和精度，采用该受力情况下的结构的应变能相对误差作为指标。应变能误差的表达式可以写为

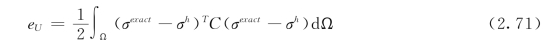
应变能的相对误差为

其中，σh是本章方法求得的应力值，σexact为精确应力值，Uexact为精确的应变能[105]。(www.daowen.com)

采用不同接触算法计算的应变能相对误差随网格尺寸的变化如图2.21所示，图中的点约束法和砂浆法+Lagrange乘子法结果来自文献[105]。由图2.21可以看出，在网格尺寸非常小时，点约束法所得结果误差比较小；但是随着网格尺寸的增大，误差也逐渐增大。本章方法与文献[105]中的Lagrange乘子法皆是基于砂浆法施加的，所得结果误差远小于点约束法误差，几乎等于零；且误差几乎不随网格尺寸变化。由此可见，砂浆法在任何网格尺寸下都能精确地施加约束条件。

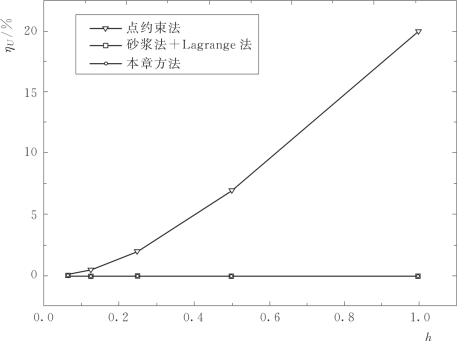
图2.21　应变能的相对误差随网格尺寸h的变化

图2.22为结构的变形图，虚线为变形前的形状，实线为变形后的形状。从图2.22可知，结构发生受压变形，由于裂纹面接触条件的施加，在受压裂纹面上没发生相互嵌入。

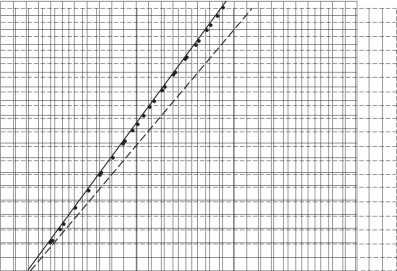
图2.22　裂纹面单元约束下的结构变形图