远处受压-剪力作用的无限大板，含一条长度为2a的中心裂纹，见图2.10。扩展有限单元法分析区域为5m×5m（图2.10），裂纹长度为2a=4m。采用四结点四边形单元，双线性等参元作为背景单元。远处压应力p=1 Pa和远处剪应力τ=1 Pa。

由于裂纹受压，故需要考虑接触条件。考虑裂纹面摩擦接触的修正的Westergaard解为[135]

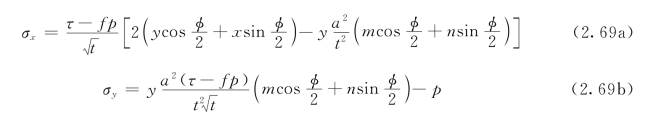
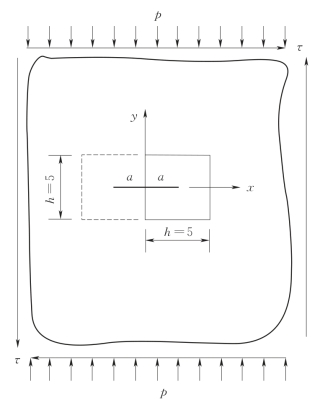
图2.10　远处受均布压应力p和剪应力τ的无限大板

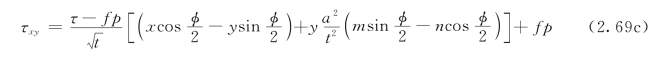
其中，m=x2-y2-a2，n=2xy，t=，φ=arg（m-in），φ∈（-π，π）。

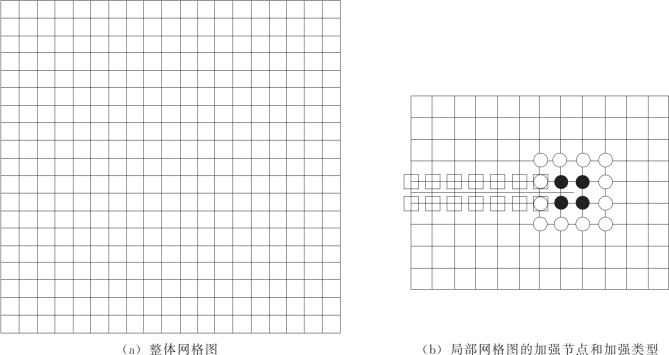
根据上述解，在5m×5m的计算域边界上施加精确的力，计算域用19×19个四边形单元进行离散（见图2.11）。标矩形的结点采用H（x）加强，标圆形的结点采用裂尖分支函数加强，标黑色圆形的结点用于计算线增函数Rα（x）。

该问题精确的应力强度因子为[135]：

(www.daowen.com)

图2.11　计算网格

图2.12为摩擦系数f=0.3时裂纹面上的法向接触应力，从图中可以看出，采用XFEM结合增广型Lagrange乘子法模拟裂纹面摩擦接触计算得到的裂纹面的法向接触应力和解析解吻合得很好；裂尖附近的接触应力值出现了稍大的误差，这可能与奇异函数的积分有关。因此，在分析受压裂纹的摩擦接触时本章的方法是可行的，而且所得结果具有较高的精确度。

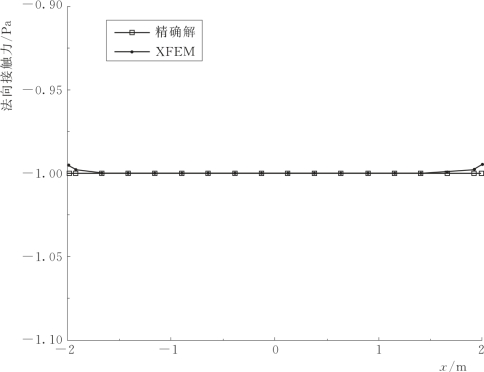
图2.12　沿裂纹面上的法向接触应力

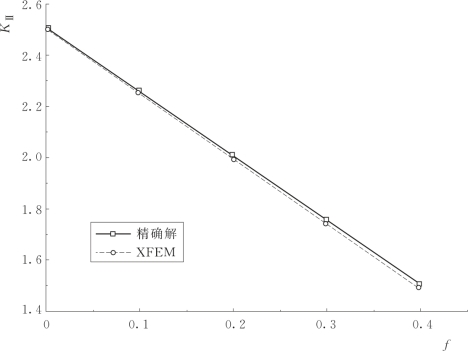
图2.13　KⅡ随摩擦系数f的变化

采用互作用积分法计算该问题的应力强度因子。图2.13给出了Ⅱ型应力强度因子KⅡ与裂纹面间摩擦系数f的关系。由图2.13可知，KⅡ和解析解中的变化趋势基本一致，随摩擦系数的增大而减小，这是由于随着摩擦系数的增大，裂纹面间的摩擦力越大，即滑动阻力也越大，这样KⅡ就减小。不同的摩擦系数f下的Ⅱ型应力强度因子KⅡ的值跟解析解的值基本一致，从而验证了本章方法的正确性及高精度性。