计算应力强度因子的方法很多，常用的有位移外推法、虚裂纹闭合法、虚裂纹扩展法和互作用积分法，其中以互作用积分法应用最为广泛，而且精度也最高。

考虑二维裂纹，裂纹用一线段描述，在裂尖建立一个局部正交坐标系。Γ为一条围绕裂尖的周线，n为周线Γ的单位外法线矢量，方向见图2.9。裂尖附近的周线积分J可表示为

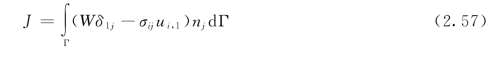
其中，W=为应变能密度。

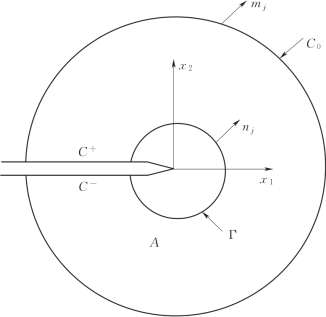
图2.9　互作用积分轮廓示意图

选择两个独立的平衡状态，状态1为真实状态，状态2为辅助状态。将两个平衡态线性叠加可得第三个平衡态，第三个平衡态的J积分为

式中：I（1，2）为状态1、2的互作用积分。

其中，为互作用应变能密度。

式（2.59）不适合数值计算，将积分项乘以一个足够光滑的权函数q（x），把式（2.59）的线积分改为一个等效的面积分，在包含裂尖的一开集内q=1，在Co边界外q=0。这样，式（2.59）的线积分可转化为下述的面积分：

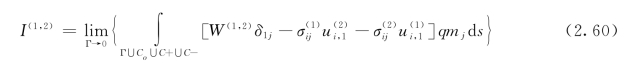
式中：mj为区域A的外法线。

区域A的边界为∂A=Γ∪Co∪C+∪C-，区域A的外法线mj为

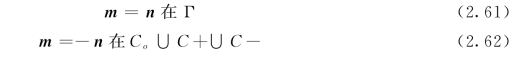
运用式（2.61）和式（2.62）和分叉理论，式（2.60）可简写为(www.daowen.com)

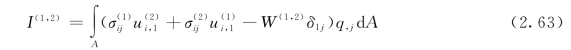
对于裂纹面上有面力作用的情况，状态1、2的互作用积分可以表示为[145]

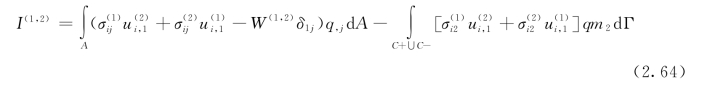
式（2.64）可用于计算水力劈裂和接触裂纹等问题的裂尖应力强度因子。

二维问题的J积分可表示为

式中：E*=E（平面应力问题），E*=（平面应变问题）。

对于第三个平衡态，式（2.65）可改写为

比较式（2.58）和式（2.66），可知：

选取状态2分别为Ⅰ型和Ⅱ型的渐近场，则可得到真实状态下的应力强度因子：

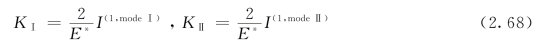
采用数值方法计算互作用积分时，积分区域A为以裂尖为圆心rd为半径的圆所穿过的单元。J积分与路径无关，但为了避免裂尖的复杂性，rd要取得足够大。建议rd取3倍的裂尖单元面积的平方根。区域A内结点的权函数q（x）=1，区域A外结点的权函数q（x）=0。

互作用积分法计算应力强度因子的详细计算过程见文献[132]。