位移模式构造后，就可以和常规有限元方法一样，由虚功原理推导其支配方程。

在外力作用下，裂纹面可能处于张开或闭合状态。当裂纹面处于闭合状态时，需要考虑裂纹面间的接触条件，否则裂纹面间会发生嵌入现象。下面推导分析接触问题的XFEM支配方程。

根据XFEM的位移逼近，式（2.31），裂纹面的相对位移uc可以表示为

式中：d为单元结点参数列阵，结点位移存在该列阵前面，结点加强变量放在后面；T为整体坐标到裂纹面局部坐标的转换矩阵；d与Nc和裂纹单元的结点加强方式有关。

其中

对于H（x）函数加强的结点

对于φα（x）函数加强的结点

式（2.15）中的增广型的Lagrange乘子场可以写成如下的矩阵形式：

式中：M为Lagrange乘子场的插值形函数。

其中，

对于H（x）函数加强的结点(www.daowen.com)

对于φα（x）函数加强的结点

另外，增广型的Lagrange乘子矩阵为

离散虚功方程式（2.27），并结合式（2.31）中的XFEM位移模式，则分析摩擦接触问题的XFEM支配方程为

其中，d=[u a b]T为结点未知量向量。

式中：u为常规结点未知量，a和b为结点附加未知量；K为劲度矩阵，来自式（2.27）的第1项；Kc为裂纹面接触劲度矩阵，来自式（2.27）的第2项；K和Kc的叠加为系统的整体劲度矩阵；F为整体荷载列阵。

K通过单元劲度矩阵组装而成，单元劲度矩阵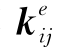为

式中：分别为常规应变矩阵、广义的Heaviside函数加强和裂尖函数加强对应的加强应变矩阵。

Kc由裂纹面单元劲度矩阵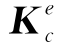组装而成

F由单元荷载列阵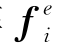组装而成