接触力的虚功方程和约束方程依赖于Lagrange乘子(λn、λτ)插值场,为了构造Lagrange乘子的插值场,本章采用线段-线段(砂浆法)的方法处理裂纹段,如图2.3所示,以裂纹和单元边界交点、裂尖点、裂纹交叉点和裂纹拐点为结点划分裂纹段单元,图中△为裂纹和单元边界交点,●为裂尖点,■为裂纹拐点,○为裂纹交叉点。根据裂纹与单元边界交点、裂尖点、裂纹拐点和裂纹交叉点处值构造Lagrange乘子场的插值。在含裂尖点的裂纹段,假设Lagrange乘子相同,即产生均匀的接触力。不含裂尖的裂纹段,Lagrange乘子呈线性变化,则Lagrange乘子场的插值可表示为:

式中:M1(ζ)=![]() ,ζ为裂纹面上的局部坐标。
,ζ为裂纹面上的局部坐标。
考虑插值得到的Lagrange乘子,式(2.12)的虚功方程用矩阵形式可表示为
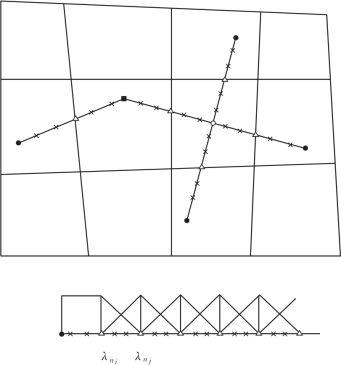
图2.3 Lagrange乘子示意图
![]()
式中:K和F为整体的劲度矩阵和荷载列阵;u为结点位移;λn和λτ为法向和切向Lagrange乘子列阵。
约束方程式(2.13)和式(2.14)用矩阵形式可表示为:
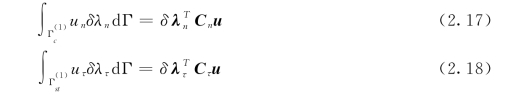
由式(2.17)和式(2.18)中的积分方程可得到Cn和Cτ。
根据虚功方程和约束方程的矩阵形式,假设裂纹面满足黏结接触条件,则系统的控制方程为:
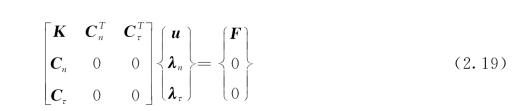
式(2.19)的最后一行对应于黏结接触条件。对于满足滑移条件的点,式(2.19)的最后一行用下式代替(www.daowen.com)
![]()
由控制方程式(2.19)可以看出,引入了Lagrange乘子以后,不仅增加了系统的求解规模,而且在控制矩阵中出现了零主元,增加了方程的求解难度。为此,Simo[129]借鉴罚函数法和Lagrange乘子法的优点,提出了求解摩擦接触问题的增广型Lagrange乘子法(在Lagrange乘子场中增加罚函数项),采用增量迭代法求解,Lagrange乘子的存在也避免了罚函数法罚因子过大而引起方程的病态。增广型Lagrange乘子的表达形式为:

式中:![]() 为法向和切向增广型的Lagrange乘子;En和Eτ为法向和切向罚因子,罚因子应选取稍大些值,以反应裂纹面间的接触,但过大的罚因子会造成劲度矩阵的病态,罚因子过小时又无法表示裂纹面间的接触不嵌入,通常选为材料弹性模量的102~105倍之间。
为法向和切向增广型的Lagrange乘子;En和Eτ为法向和切向罚因子,罚因子应选取稍大些值,以反应裂纹面间的接触,但过大的罚因子会造成劲度矩阵的病态,罚因子过小时又无法表示裂纹面间的接触不嵌入,通常选为材料弹性模量的102~105倍之间。
摩擦接触是高度非线性的,需要迭代求解。在上述增广型Lagrange乘子法中,通过反复的非线性迭代,直至迭代收敛,收敛时增广型Lagrange乘子的控制方程的解逼近于真实的接触约束力。
假设结构产生一个虚位移v,其虚功方程可以表示为
![]()
式中:u为满足位移边界条件的真实位移场函数,u和结构的虚位移v满足:
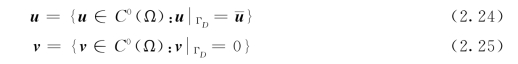
裂纹面的相对位移为uc=v+-v-,式(2.23)可以改写为
![]()
把增广型Lagrange乘子场代入式(2.26),可得
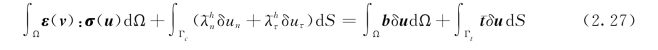
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







