裂纹体受压时，裂纹面由于压力的作用可能会引起裂纹的闭合，在闭合裂纹面上则需引入裂纹面的接触条件，避免裂纹面发生相互嵌入。考虑二维问题，可能发生接触的两个裂纹面记为，裂纹面间存在的接触力如图2.1（b）所示。为了系统地分析裂纹面接触条件的施加方法，在裂纹面上建立局部坐标系（见图2.2）。假设为小变形，设上、下裂纹面上接触点对的接触应力表示为pn和pτ；接触点对的位移为和

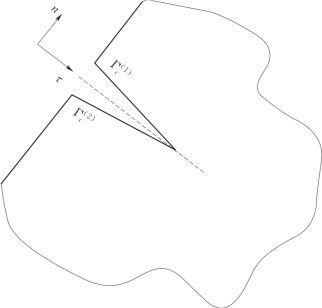
图2.2　裂纹面的局部坐标

裂纹面上接触点对的法向和切向相对位移可以表示为

对于弹性接触问题，裂纹面的接触力和相对位移之间的关系要满足接触不嵌入条件，则满足Coulomb定律的接触力和裂纹面相对位移的关系可以用下列等式和不等表示如下[127，128]：

式中：f为裂纹面间摩擦系数；un≥0表示接触面不发生相互嵌入；pn≤0表示发生接触时裂纹面间的应力为压应力；pn=0时，裂纹面沿法向发生分离；=0时，裂纹面沿切向发生接触滑移；时，裂纹面无滑动，处于黏结状态。

接触问题可描述为求区域内位移场，使得系统的势能达到最小。Lagrange乘子法是求解接触约束最小化问题的主要方法之一，通过引入Lagrange乘子将接触问题转化为无约束问题求解。接触状态有三种：张开、黏结、滑移。法向Lagrange乘子场λn表示当接触发生时迫使un等于零（裂纹面接触不嵌入）的压力，切向Lagrange乘子场λτ表示在黏结区迫使满足黏结条件的切向力。当裂纹面发生摩擦接触时，接触面分为黏结区和滑移区。在滑移区，接触应力满足Coulomb摩擦定律。(www.daowen.com)

应用Lagrange乘子法在裂纹面添加摩擦接触条件时可以导出三个方程：

（1）第一个方程是内外力的虚功必须等于零，即

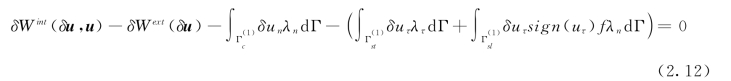
（2）第二个方程是接触不嵌入条件，即

（3）第三个方程是黏结条件，即

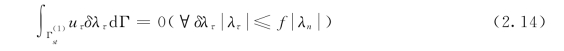
在式（2.13）和式（2.14）中，接触压力必须是压应力，即λn≤0。