1.MFD 模型

基于快速路通道的MFD 模型，可以对快速路的宏观交通流状态进行等级划分。文献[4]参考了拥堵感知调研的速度阈值划分结果，根据MFD 中散点分布位置，将快速路的宏观交通流状态划分为I～V 五个等级。这五个等级的流量、密度参数阈值如图8-3所示。该图中，交通流密度越大，对应的等级越高，拥堵越严重。

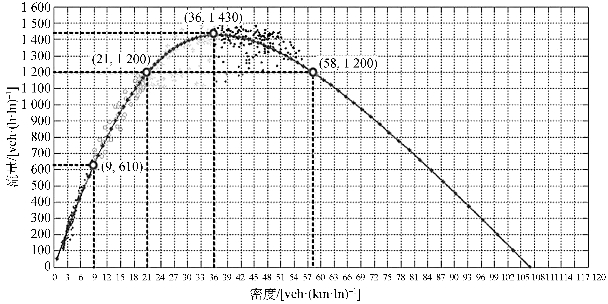
图8-3　基于MF D 的快速路交通流状态等级划分［4］

这五个等级下的交通流状态特征及拥堵风险如表8-5所列。

表8-5　五个等级下的交通流状态特征及拥堵风险［4］

(续表)

2.速度分布

文献[4]还研究了基于速度分布的交通流状态等级划分方法。这种方法需要采集快速路上的浮动车(主要指出租车等营运车辆)数据，由于浮动车数据覆盖范围广，所以能较好地反映快速路上绝大部分车辆的运行状况。

在任意一个时间间隔内，若快速路某路段的浮动车平均速度为vi，则其对应的单位里程行程时间为ti(单位为min/km)，二者满足ti=1/vi。不同路段的单位里程行程时间不同，因此存在单位里程行程时间随里程变化的概率密度函数f(t)。可以将单位里程行程时间均匀地划分成小段(如每隔6 s划分一段)，通过统计每一段上有多少路段里程落在上面，从而得到单位里程行程时间的里程比例分布。分别采用正态(Normal)、对数正态(Lognormal)、伽马(Gamma)和韦布尔(Weibull)四种常用分布进行曲线拟合(图8-4)，从而确定了快速路上车辆单位里程行程时间的里程比例分布服从对数正态分布函数：

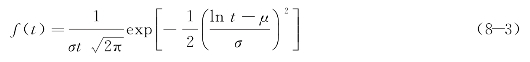
式中 t——车辆单位里程行程时间，min/km；

μ，σ——分别为快速路单位里程行程时间概率分布模型的平均值和方差，满足t ＞0，σ ＞0，-∞＜μ ＜+∞。

对于任意时间，μ和σ可以通过对所有车流单位里程行程时间的对数进行统计计算获得，分别为ln t的期望值和标准差，计算公式为

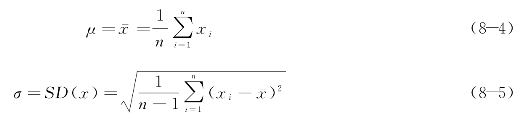
式中 xi——单位里程行程时间ti的对数，即xi=ln ti；

n——研究时段内快速路上单位里程行程时间的取值个数；(www.daowen.com)

x-，SD(x)——分别为研究时段内单位里程行程时间的对数的均值和标准差。

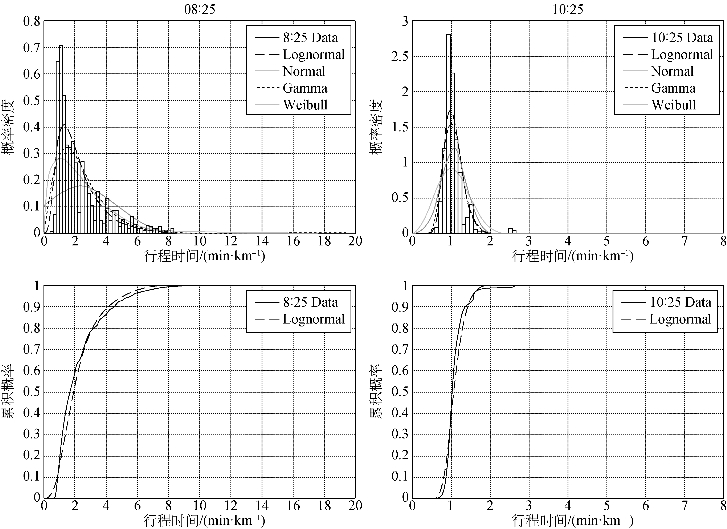
图8-4　单位里程行程时间概率分布［4］

在给出单位里程行程时间的里程分布的概率密度函数之后，累积概率分布函数可以表示为

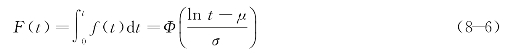
又因为快速路运行速度vi的累积概率分布F(vi)可表示为

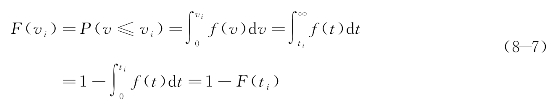
故快速路上车辆运行速度的累积里程概率分布函数为

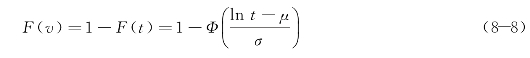
通过采集北京西三环快速路的浮动车数据，得到每隔10 min的车辆运行速度累积里程概率分布，3天共得到432条概率分布曲线，如图8-5所示(不同的灰度表示不同状态等级)。其中，横坐标表示车辆运行速度，且取值由高到低，对应单位里程行程时间由0向∞；纵坐标为运行速度的累积概率。图中不同灰度的线条落在坐标系的不同区域，这说明当快速路宏观交通流状态不同时，车辆运行速度的里程分布也不同。

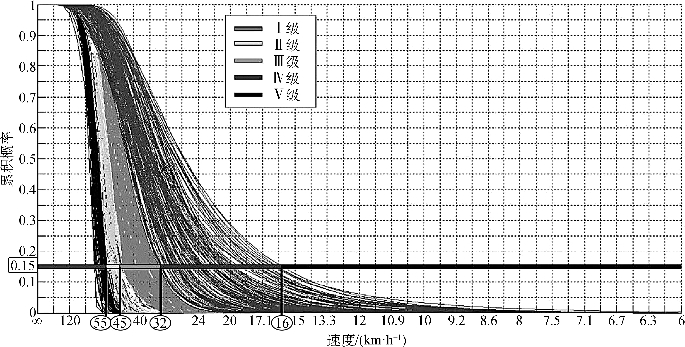
图8-5　基于速度分布的宏观交通状态等级对应速度阈值划分［4］

设曲线上的任一点的纵坐标取值为F(vi)，表示快速路上以小于(含)速度vi所完成的车辆行驶里程的总比例。定义F(vi)=15%为临界点，将其对应的速度值vi作为评价快速路宏观交通流状态的自变量，即该时间段内的车辆行驶里程中有85%的运行速度不低于vi。将vi作为评价快速路宏观交通状态的自变量，不同状态等级对应的速度阈值如图8-5所示(也可见表8-6)。这里五个等级的含义与表8-5相同。

当然，速度阈值的确定除了这种方法外，还可以直接参考相关标准。北京市地方标准《城市道路交通运行评价指标体系》(DB11/T 785—2011)[5]也将快速路交通流状态划分为了五级，相应的速度阈值见表8-6[6]。

表8-6　基于速度阈值的快速路交通流状态等级划分

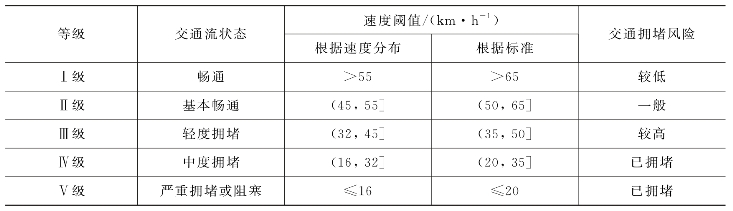
由此可见，相比于标准给定的速度阈值，根据速度分布统计方法得到的速度阈值在拥堵状态的判别和评估上更为保守一些，但总体差别不大。这里介绍的速度分布统计方法的好处是，具有更强的普适性，即对于不同城市的快速路，只需按照这个方法重新收集、统计和处理数据，就可以得到适用于该城市快速路的交通拥堵状态速度阈值划分标准。