Wardrop在1952年提出了经典的网络均衡分配的第一准则和第二准则，即用户均衡(User Equilibrium，UE)和系统最优(System Optimum，SO)。

1.用户均衡

Wardrop第一准则(UE)假设出行者都确切知道网络的交通状态并选择最短路径出行。在UE状态下，所有出行者都不会通过单方面改变路径来降低其行程时间。Beckmann等学者提出了与UE等价的数学规划表达式：

式中 A——路段集合；

R——起点集合；

S——终点集合；

K rs——OD 对(r，s)间的路径集合；

ta(ω)——路段a 的阻抗函数，是路段流量ω 的函数，常采用BPR(Bureau of Public Road)函数的形式：

t0——自由流状态下路段的行驶时间，h；

c——路段通行能力，pcu/h；

α，β——公式中的参数(常用值是0.15和4)；

xa——路段a 分配的流量，pcu/h；

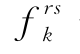——OD 对(r，s)间路径k 的流量，pcu/h，决策变量；

qrs——OD 对(r，s)间的总流量，pcu/h；

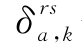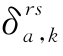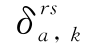——路段-路径关联变量，如果路段a 在OD 对(r，s)间的路径k上，则=1，否则=0。

上述模型中的三个约束条件分别为：式(7-11)表示OD 间各条路径上的流量之和等于OD出行量；式(7-12)表示任意路段的流量等于途经它的全部路径流量之和；式(7-13)表示路径流量非负。可以证明，上述模型的解满足所有使用路径的阻抗相等且最小，未被使用路径的阻抗都不小于使用路径的阻抗。在实际工程项目应用中通常采用用户均衡交通分配法。(www.daowen.com)

上述模型的求解通常采用Frank-Wolfe算法，步骤如下：

第一步，初始化。按照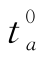=ta(0)，∀a，进行全有全无交通分配，得到各路段流量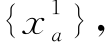，令n=1。

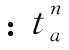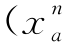第二步，更新各路段阻抗=ta)，∀a。

第三步，寻找迭代方向。按照更新后的{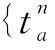}，执行全有全无分配，得到一组附加流量。

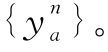第四步，确定移动步长。求解满足如下一维线性搜索问题的最优λ(可采用黄金分割法或二分法等)。

第五步，确定新的迭代点。

第六步，收敛性检验。如果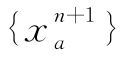满足规定的收敛准则[式(7-16)]则停止计算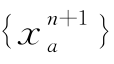，即为最优解；否则令n=n+1，返回第二步。

在得到UE交通分配结果后，就可以这个结果为目标，通过交通信息诱导等手段，引导网络向这一目标靠拢，尽可能地实现网络用户均衡。

2.随机用户均衡

随机用户均衡(Stochastic User Equilibrium，SUE)进一步考虑了用户对阻抗感知的随机性。在SUE中，路径选择概率与路径感知阻抗有关，路径感知阻抗是实际阻抗(和流量相关)与感知误差的和。如此反馈，达到SUE状态，这个关系也被称为SUE 条件。SUE 比UE 更具普适性，UE可被看作是SUE的一种特殊情形(即感知误差为0)。

3.系统最优

Wardrop第二准则假设，在SO 状态下，网络总出行成本(或平均出行成本)最小。SO 的数学规划表达式与UE具有完全相同的约束条件，唯一不同之处在于目标函数。SO 的目标函数可以等价写为

因此，可以简单修改UE问题的Frank-Wolfe算法，用路段边际行程时间替换ta(xa)，即可求解SO 交通分配模型。

无论UE还是SO，其目标都是尽可能降低路网的总体阻抗，只是侧重的角度略有不同而已。因此，UE和SO 都是较好的路网均衡状态，都有利于最大限度地防控交通拥堵风险。