在道路网络交通流状态的研究中，常常会引入宏观基本图(Macroscopic Fundamental Diagram，MFD)的概念。

与传统交通流基本图不同，交通流宏观基本图关注道路网络层面上交通流三参数(流量、密度、车速)之间的关系和性质。2007年，C.F.Daganzo和N.Geroliminis[8]通过研究日本横滨的数据发现，单个检测器数据的流量-占有率关系具有很大的离散性，见图7-1(a)。然而，将整个网络的所有检测器的流量和占有率集聚后，可以形成一个离散度很小的曲线，见图7-1(b)，并基于此验证了MFD 的存在性。由此引发了学术界对MFD 的广泛关注，并使其逐渐成为一个新的研究热点。

C.F.Daganzo和N.Geroliminis认为，MFD 具备三个基本性质：

(1)道路网内平均交通流量和平均交通密度(占有率)之间存在与交通流基本图类似的抛物线关系。

(2)网络平均流率与网络总输出流量之间存在稳定的线性关系。

(3)MFD 是网络交通流的固有性质，由网络基本设施形态及交通控制决定，而与交通需求无关。

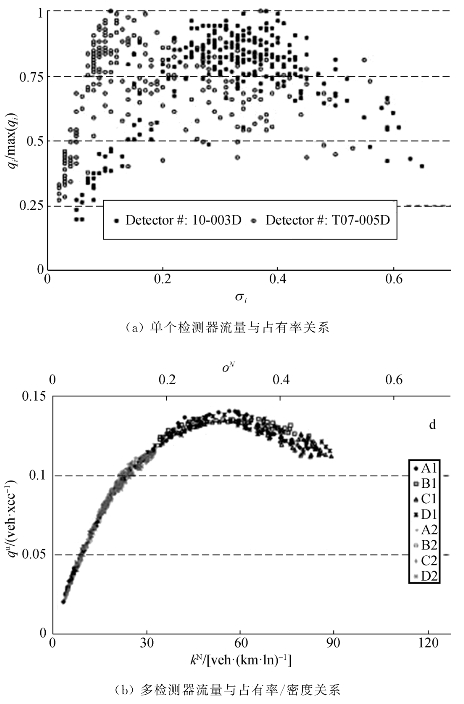
图7-1　道路网络MF D

MFD 反映了整个网络交通量与网络运行水平的普遍关系，其不仅仅描述了网络流量与占有率的关系，也反映出网络内车辆数和流出网络的车辆数之间的关系，以及车辆运行里程与运营时间之间的关系等。通过对MFD 的分析，C.F.Daganzo发现其基本曲线形式为抛物线，但在实际的分析中常简化为三角形或梯形。

此外，C.F.Daganzo在提出MFD 时指出，一个网络只有在其内部交通状态处于“同质性”时，即整个交通小区要么全部处于拥挤状态要么全部处于非拥挤状态，才存在离散度低的MFD。随后，大量学者就各种原因导致的网络“非同质性”对MFD 的影响展开了研究，探索了不同因素对MFD 离散度的影响。

现有研究表明，MFD 的影响因素主要包括四个方面：道路设施、交通条件、管控条件以及路径选择行为。本质上，所有影响因素皆因引发网络密度的改变，从而最终对MFD 产生影响，形成“滞回现象”[9]。所谓“滞回现象”就是流量与占有率的比例关系图为封闭曲线，而不是线性曲线。引起这种现象的主要原因为网络密度的不均匀性。进一步的研究指出，网络密度分布的不均匀是导致路网通行能力不高的主要原因，而网络密度均匀化能够提高网络的通行能力与整体性能[10]。

因此，基于MFD 的理论分析与实际验证，提升路网通行能力的核心方法是提升路网密度的均衡性。而要实现这一目标，主要有如下几种措施：优化路网结构、合理引导路径选择和实施可变车道等。

1.优化路网结构

研究表明，路网结构会影响MFD 的形状及网络密度的均匀化。

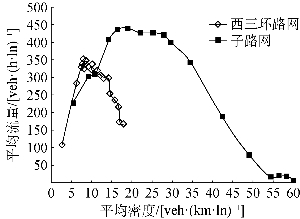
图7-2　不同路网平均流量-平均密度关系

文献[11]通过构建北京西三环路网及其子路网交通流的MFD 模型，研究了不同区域路网宏观交通状态的差异。对比两个不同范围的路网：第1个路网是西三环区域路网，区域内包含快速路、主干路、次干路和支路等不同等级和功能的路段；第2个路网为西三环子路网，仅包含快速路交通走廊及一定范围内的相交道路。分别向两个路网加载相同背景的交通需求，仿真得到路段的流量和密度，集成路网平均流量和平均密度，绘制两个路网的平均流量-平均密度关系，如图7-2所示。

显然，两个路网的平均流量-平均密度关系图不同。对于西三环大路网而言，路段数量多，等级差别大，且非干道型的次干路和支路比例较大，不同等级道路上车流状况差异大，集成后的路网平均流量、密度值偏小，得到的路网通行能力、阻塞密度均较低。然而，子路网范围小且大部分路段为快速路或主干路，路面交通状况差异小，因此路网平均流量及密度均偏高，通行能力、阻塞密度较高。

由此可见，对于不同规模和结构的路网而言，宏观交通状态差别较大。路网结构越均匀，各路段交通状态差异越小，路网整体性能越高。因此，从网络规划的层面考虑，应优化路网结构，引导交通出行向主干道、次干道、支路等道路均衡发展，协调各等级道路之间的功能，从而提高路网的实际服务能力。相关内容可参考本书6.1.2节。

2.合理引导路径选择

出行者不同的路径选择行为同样会对MFD 产生影响。

文献[11]选择INTEGRATION 模型中的个体反馈选择方式和分组反馈选择方式，分别进行了情景仿真。绘制两种路径选择方式下的路网车流密度时空分布图和平均流量-平均密度关系图，如图7-3所示。

图7-3　不同路径选择方式下平均流量-平均密度关系

由此可见，不同路径选择方式影响了路网MFD 的形状，改变了路网阻塞密度。当出行路径选择分组反馈方式时，运行中的大部分时间内，路网平均流量在通行能力处波动，之后随着路网密度增大，平均流量迅速下降；选择个体反馈方式时，路网平均流量达到通行能力后便呈现出持续下降趋势，但流量下降速度较慢，路网平均密度也持续升高，且阻塞密度远大于分组反馈方式。

由此可见，驾驶人路径选择方式是影响路网宏观交通状态的另一个重要因素，它不仅改变了路网内交通拥堵的时空分布情况，也影响了路网宏观交通状态。据此，交通管理者可结合路网宏观交通状态及变化规律，引导居民调整出行习惯，并通过实施先进的交通信息诱导策略引导驾驶人选择合理的出行路径，从而提高路网整体交通性能和服务水平。(www.daowen.com)

3.实施可变车道

可变车道通过临时改变某条车道的交通流方向，最大限度地利用未饱和车道的道路资源，以提高拥堵路段的通行能力。如图7-4所示，实施可变车道前，由东向西车道的车流密度远大于由西向东车道的车流密度，拥堵严重；实施可变车道即将由西向东的一条车道改为由东向西后，通过变换一条车道的方向，使由东向西车道的通行能力提高约50%，双向的密度也更加均匀。因此，对于双向交通流不均衡的情况，实施可变车道是提升网络密度均衡性的有效手段。

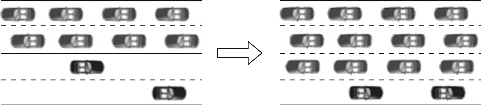
图7-4　可变车道示意图

对于单个路段的调整是很容易实现的，但是对于一个城市的交通网络来说，某时段内可能存在十几段或几十段双向流量不平衡的路段，而其中任一路段上车道方向的调整都会引起整个路网交通流量的变化，这些路段的调整是相互影响的。因此，不能孤立地着眼于一条路段的调整，而忽略其他路段，必须从系统角度，根据实际交通需求的变化来确定这些路段的车道调整方案，以达到交通网络系统性能指标最优。对路网层面而言，实施可变车道的目标可以定为：对于给定的道路网络、车辆位置和目的地，每个车道分配一定的交通流，使得网络效率最大化。

文献[12]将该问题视为最大的多物网络流问题，提出了整数线性规划和双层规划模型计算网络的通行能力。这里介绍整数线性规划模型。

将道路网络视为由边、节点组成的图G={V，E}，其中V 表示节点集合，E 表示边集合。在实施可变车道的条件下，该网络满足以下约束条件：

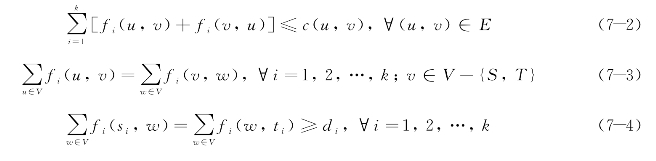
式中 i——路网中的某一条交通流(OD 对)，一共有k 条；

(u，v)——起点为u、终点为v 的边；

c(u，v)——边(u，v)的双向通行能力，pcu/h；

fi(u，v)——第i条交通流经过边(u，v)的流量，pcu/h；

u，v，w——节点；

si——第i条交通流的起点；

ti——第i条交通流的终点；

S——所有起点组成的集合；

T——所有终点组成的集合；

di——第i条交通流的交通需求，pcu/h。

式(7-2)表示任意一条边两个方向的流量不得超过这条边的双向通行能力，由于实施了可变车道，两个方向的通行能力可以灵活分配。式(7-3)表示除了起点、终点外的任一节点交通流的流入等于交通流的流出。式(7-4)表示各条交通流从起点流出的流量等于流入终点的流量，且必须达到或超过交通需求。

该模型的目标是最大限度地提高路网的总流量，即

试验表明，相比于没有重新配置车道，经过一定程度的重新配置车道(实施可变车道)，路网的通行能力有显著提高，同时进一步证实了路网通行能力的提升是由高频率的车道变换实现的。低频率的车道变换测试(每隔3～5 h配置车道一次)的结果显示，该种模式下路网通行能力可以提高约12%；在高频率的车道变换测试中，如果每隔2 h配置车道一次，路网通行能力可提升约33%；如果每隔1 h配置车道一次，路网通行能力增长更是高达72%。当然，频繁地配置车道会引起驾驶人的不适应，可实施性不强，但也足以表明，快速适应交通流情况的可变车道变换技术可有效提升道路网络的通行能力。

4.其他措施

有研究表明，还有一些别的因素会影响MFD 及路网密度。例如，交叉口左转交通流的存在会减小MFD 的最大值，因此对于左转流量大的交叉口而言，可以考虑设置左转专用相位、左转待行区和左转导流线，以提高左转车流的通行能力。在一些关键交叉口，甚至可以考虑采用禁左措施。还有研究探索了不同比例公交及私人小汽车出行对MFD 离散度的影响，发现小汽车出行比例越大，曲线离散度越大，这意味着网络密度不均衡性越大，因此为提升网络密度的均匀性，应提高公交出行比例，严控小汽车的出行比例。