交通事故的持续时间是评估事件对路网的影响范围和造成的交通延误的主要依据。交通事故持续时间可划分为四阶段,包括:事件检测时间、事件响应时间、事件现场清理时间和交通恢复时间,如图5-3所示。
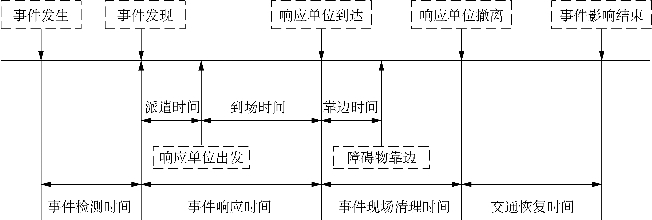
图5-3 交通事件持续时间分段
1.事件检测时间
事件检测时间指从事件发生至接到事件报警的时间段。
假设正常情况下,路段通行能力为C0,到达流量为Q0,由于发生了交通偶发事件,导致道路通行能力降为C'。定义事件状态下的高速公路路段通行能力折减系数为λ(λ 的取值可参照HCM2016给出的数值),则事件发生情况下的路段通行能力为
![]()
由线性交通流的Greenshields模型

求解得到

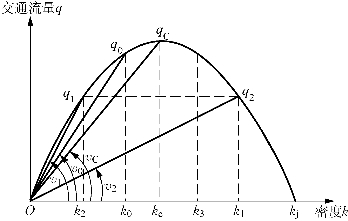
图5-4 事发点交通流量、密度及速度的关系
式中 v——车速,km/h;
k——密度,veh/h;
vf——自由流车速,km/h;
kj——阻塞密度,veh/h。
事件发生前路段交通状态为P0(k0,v0,q0),事件发生后,下游处的交通状态为P1(k1,v1,q1),上游处的交通状态为P2(k2,v2,q2)。密度基于线性交通流的偶发事件的事发点处的交通流量、密度及速度的关系如图5-4所示。
事发点的交通量q1=q2=λC0=λkjvf/4。由线性交通流模型给出的流量-密度-速度的基本关系式为q=kv=kvf(1-k/kj),令β=k/kj,则:
![]()
式中,qc表示最大流量。
解关于β 的一元二次方程得
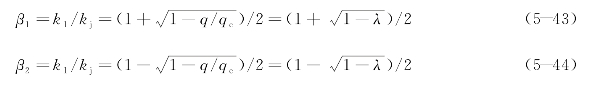
根据经典波速公式,即式(5-26)可知,事件发生后,向上游传播的集结波波速W1和向下游传播的消散波波速W2分别为
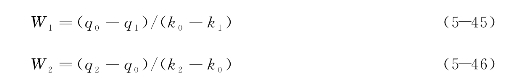
再根据以上公式进一步得出
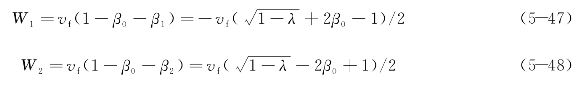
式中,β0=k0/kj。
设事件发生点与上游检测器的距离为L1,与下游检测器的距离为L2,若采用双截面检测法来检测事件,事件的平均检测时间MTTD(Mean Time to Detection)的计算如式(5-49)所示。
![]()
式中 T(A)——检测算法的反应时间,即当事件产生的集散波到达事件检测器时至被检测出的时间,s;
Te——其他影响因素产生的延误时间,s。
由此可知,事件的平均检测时间与事发点距离上下游检测器的距离、事件波的传播速度、检测算法的反应时间等因素相关。
2.事件响应时间
事件响应时间指最先参与清除过程的车辆类型中第一辆车的到场时间。
这里通过一个实例进行说明。采用华东地区某高速公路交警支队2006年的事件记录和接出警记录。事件数据集中包含545条事件数据,记录了事件处理过程中的报警时间、交警到场时间、车辆靠边时间、现场撤除时间以及事件特征和环境特征,包括:事件发生的日期、时间、当时的天气、事件类型、占据车道数、需要的救援车辆、报警方式、伤亡人数、当事车辆种类等。通过查阅相关接出警记录可以补充一些必要的信息,包括各种救援车辆的到场时间、事发地点的桩号等。
数据与处理包括有效数据的筛选、相关因子的确定及因子水平的划分。数据预处理后得到400条有效数据,随机选择其中40条数据作为检验数据,其余为训练数据。在描述事件特征的诸多参数中,部分参数是直接影响到场时间的因子,而另一部分为间接影响到场时间的因子或与到场时间无关的因子。在排除间接因子后,可利用散点图、盒状图、相关分析及方差分析来筛选直接因子。事件发生的时间、救援车种与到场时间的盒状图如图5-5所示。
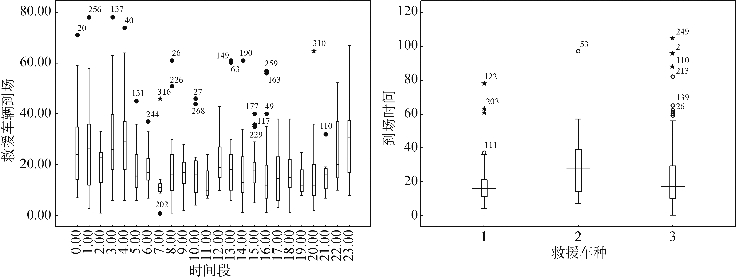
图5-5 事件发生时间、救援车种与到场时间的盒状图
由图5-5可知,事件发生的时间、救援车种与到场时间之间存在联系,并且可以直观判断,夜间事件的到场时间大于白天事件的到场时间,涉及吊车的到场时间要长于救护车和拖车。通过直接影响因子分析,影响到场时间的因子主要有两个:事发时间段和救援车辆种类。为了区分不同时段对到场时间的影响,将影响相近的时间段归类,得到相关因子水平如表5-1所列。
表5-1 相关因子水平及其描述

由于最终确定的相关因子只有两个,且因子水平只有七类,故采用到场时间的范围预测而非常见的值预测,否则只能求出有限多个预测值,无法满足后续研究和实际应用的需要。相应的预测方法应为概率方法或分类方法而非参数回归方法。七类因子水平下到场时间分布频率的直方图如图5-6(a)所示。
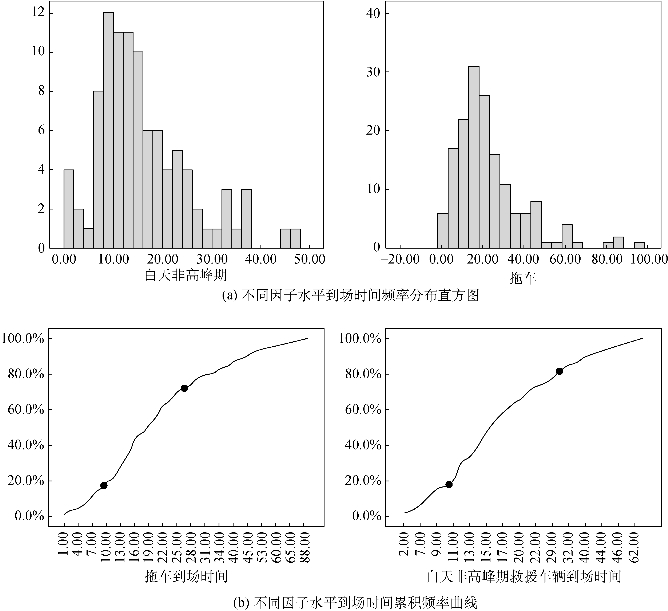
图5-6 不同因子水平到场时间(https://www.daowen.com)
图5-6(a)显示在所有因子水平下的到场时间频率都具有形如威布尔分布或对数正态分布的曲线形式。威布尔分布的累积分布函数如式(5-33)所示。

式中 m——形状参数;
a——尺度参数。
然而,相关研究成果尚未发现到场时间服从何种分布。考虑到场过程并非连续单一的线程,而是由若干子过程构成的,每一个子过程的运作方式和影响因素又不尽相同,故不采用分布曲线拟合的方式来进行预测,仅将分布曲线作为参考。由分布函数可以看出,诸如威布尔分布或对数正态分布的累积分布曲线通常含有一个拐点,拐点一侧自变量范围较小,但累积频率较大,这一侧往往是样本值的常见覆盖范围,另一侧则相反。部分因子水平下到场时间的累积频率曲线如图5-6(b)所示。
由图5-6(b)可以看出,每条曲线含有两个拐点,约60%~80%的样本值都在这两个拐点之间,而两个拐点之间的时间范围往往在20 min左右。通常情况下,可以采用多项式拟合累积频率曲线P=a+a1t+a2t 2+a3t 3+…+ant n,并求二阶导数以获取拐点位置。根据样本数据计算所得的各因子水平下该区间的上下限及相应到场时间的均值如表5-2所列。
表5-2 不同因子水平拐点区间上下限及其均值
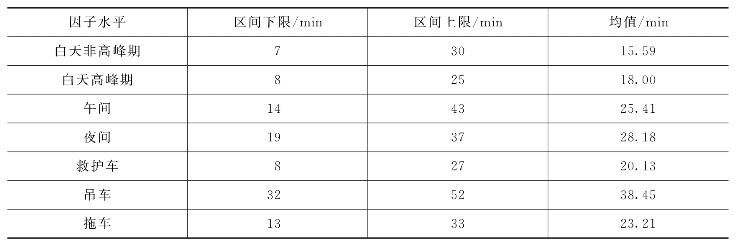
由表5-2可知,吊车到场时间主要分布在32 min到52 min之间,如果事件发生在白天非高峰期,则可认为其到场时间累积频率曲线上限拐点右侧部分是由吊车贡献的,而相应的下限拐点左侧部分则大多数由救护车贡献。基于这样的想法,将时间段因子水平与救援车辆因子水平拐点上下限进行组合,得到到场时间预测区间如表5-3所列。
表5-3 到场时间预测区间
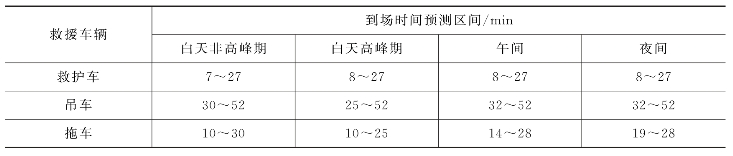
将剩余40条数据组成的样本检验组来对比实际值与预测值,如图5-7所示,检验数据有80%以上的样本都落在预测区间之内,说明该模型能够有效地预测事件的到场时间。
3.事件现场清理时间
根据前文事件响应时间的新定义,基于救援车辆的清除时间可定义为:交通事件发生后,从第一次序救援车辆到场至当事车辆靠边或被清除的时间。这个定义考虑了真正实施现场清理工作的时间节点问题,更加紧密地同交通事件影响范围的研究相结合。本节采用基于人工神经网络的TSK 型模糊逻辑系统来进行清除时间预测。
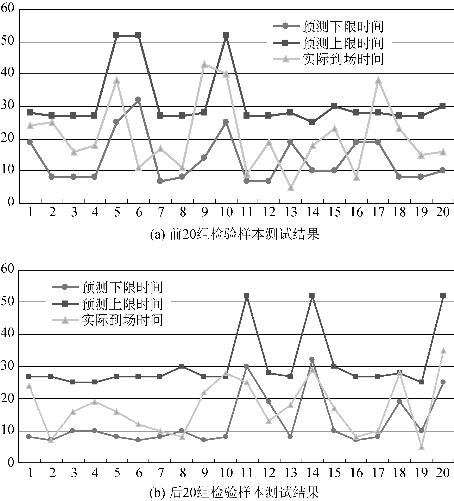
图5-7 模型预测值与实际值的对比
数据预处理应根据人工神经网络——TSK 模糊逻辑建模的特点进行。本节利用MATLAB提供的ANFIS方法进行建模。数据预处理主要包括两方面:去噪和降维。通过数据预处理过程,最终筛选出200条有效数据,同时将影响因子合并成三类,这样就极大地减少了模糊规则的数量,也减少了模糊模型的计算工作量。
建立TSK 模型时,最重要的是初始FIS结构的确立。因为人工神经网络训练不会改变模型的结构,只会改变参数的值,因此初始模型结构即为最终模型结构。令P,V,E 为模型三个语言变量的论域。根据样本数据可得三个论域取值范围分别为[0,6],[0,9],[1,10]。采用三个模糊集表征因子水平由低到高的变化,同时设定三个模糊集间的算法为和取(and method),则可以确立模型的整体结构,如图5-8所示。
可以看出,三个输入变量通过模糊化和逻辑推理后,得到输出变量的33 个模糊集。最终通过这些模糊集的加权线性叠加,将输出变量清晰化(defuzzification),使之综合为一个输出值。模糊集是由模糊变量和隶属函数决定的。在ANFIS方法中隶属函数的参数是通过人工神经网络训练得到的,因此只需手动选择隶属函数的类型。常见的隶属函数形式有三角隶属函数、梯形隶属函数和高斯隶属函数。本文选择更为平滑的高斯隶属函数,其表达式如下:
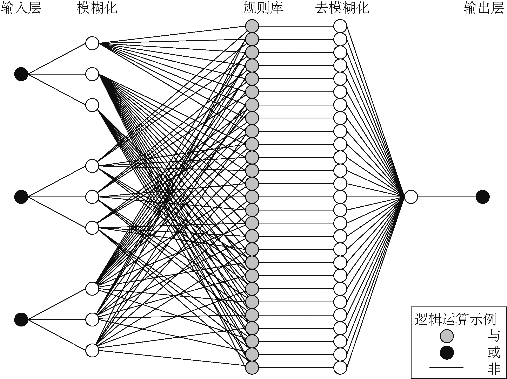
图5-8 模型整体结构
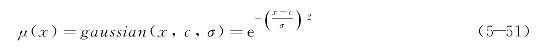
式中,c 表示隶属函数的中心;σ 决定了隶属函数的宽度。ANFIS方法的重要步骤是采用自适应算法拟合隶属函数的参数值。将样本数据按清除时间由小到大进行排序,按各行选取法选取训练数据,其余作为检验数据,取最大训练次数为50次,即可用训练数据对初始FIS进行训练。通过多次试算,最终得到一个相对精确的清除时间预测模型。模型训练误差随训练次数的变化如图5-9所示。
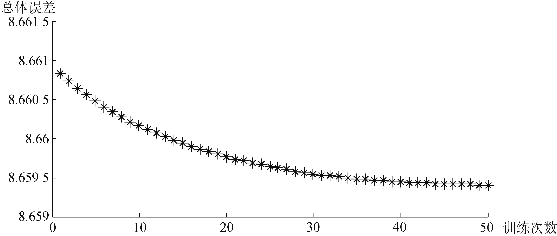
图5-9 模型训练误差收敛过程
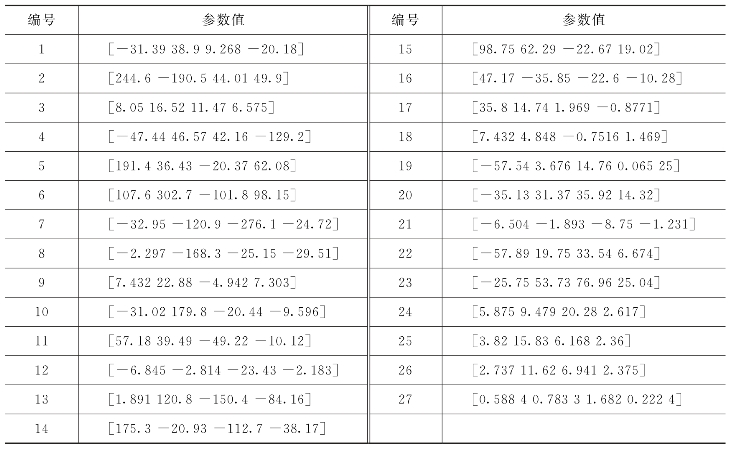
由图5-8可以看出,尽管误差收敛过程非常缓慢,但随着训练次数的增加,总体误差是呈减小趋势的。这说明训练数据中输入变量和输出变量之间确实存在一个模糊关系,可以通过输入值大致地推断输出值。表5-4列出了预测模型中输入变量隶属函数的参数值。输出函数参数值见表5-5所列。
表5-4 输入变量隶属函数参数值
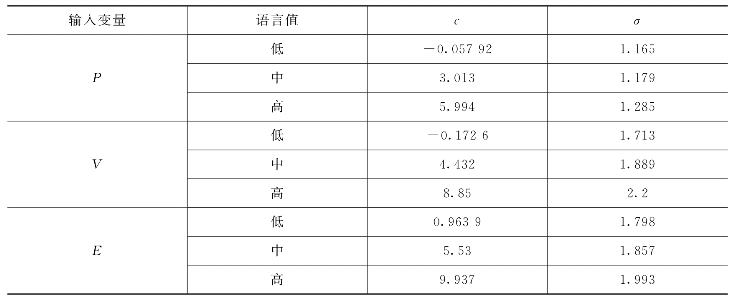
表5-5 输出函数参数值
由此可得,当交通事件的当事人员、当事车辆和救援车辆特征已知时,即可用上述TSK 模糊逻辑推理模型预测事件的清除时间。ANFIS是一种基于已有数据的建模方法,建立的模糊系统模型的预测结果能否很好地模拟这些数据是检验此模型的最好方法。对预测模型进行检验,得到样本值和预测值的散点图,如图5-10所示。其中,菱形代表清除时间样本值,星形代表模型预测值。
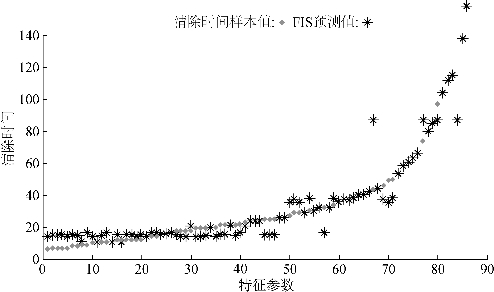
图5-10 清除时间样本值与预测值散点图
可以看出,当样本值随事件当事人员、当事车辆和救援车辆特征参数变化时,预测值能够很好地模拟这种变化趋势,并且在清除时间不太短时取得了较好的预测效果。然而,当清除时间小于20 min时,预测效果并不理想。样本值越低,误差越大。经研究分析,出现这种情况的原因主要有两点:
(1)清除时间本身是一个具有较强随机性的变量,它唯一的确定性限制规则是所有参与清除的人员都试图尽快地结束清除工作。然而,清除过程的任意环节都包含随机误差,甚至事件记录人员对于事件处理起始和结束点的理解也是误差来源之一。当事件清除时间较长时,随机误差与样本值的比值尚未达到产生严重偏差的地步,但清除时间较短时,这个误差值往往是无法忽视的,甚至会超过样本值本身。此时,对于清除时间的预测不再具有实际意义。当然,短时间内事件对于路网的交通影响通常也较小。
(2)在事件记录和计算建模过程中,部分事件特征信息丢失。为了简化模型,降低计算工作量,选取的只是对清除时间具有显著影响的变量因子,而其他非显著因子则被忽略。对于短时间事件来说,每一个因子的影响都可能会被放大,这也是造成误差偏大的重要原因。
4.交通恢复时间
交通恢复时间的定义为从事件处理完毕到事件对路网的影响完全消散的时间。
根据确定性排队理论,在得知前几个阶段的持续时间后,可以推算出交通恢复时间。如图5-11所示,当事件发生后,可以认为前两个时间段内交通状况不发生变化,即在事件检测时间段和事件响应到场时间段内,事件上游车辆到达和离去的流率不变,故可以合并为一个时间段T1来考虑。此处简化过程直接给出交通恢复时间结束时刻的计算公式,如式(5-35)所示[10]。
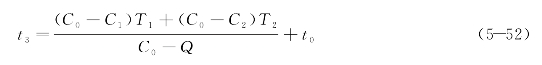
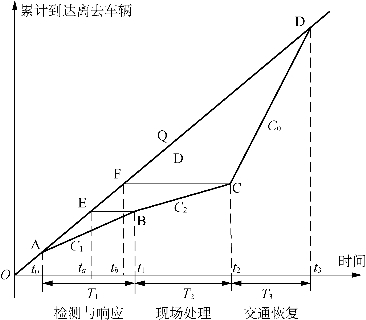
图5-11 事件上游车辆到达离去曲线图
此时,交通恢复时间T3的预测式为
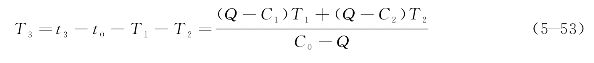
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







