交通波理论是基于模拟流体连续方程而建立的一种车流连续方程，用水流的起伏状态比拟道路上运行的车流变化。与水波的起伏波动相同，当车流密度产生变化时，车流将以不同的密度进行传播，就会形成交通波动现象[7]。交通事故发生后，事故地点前后的车流密度在此后一段时间内持续发生改变，进而产生车流的集结与消散，这一过程可以用交通波理论进行分析。

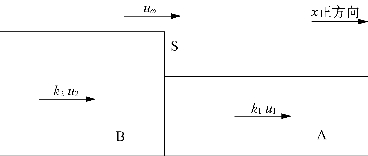
图5-2　两种密度的车辆运行状况

假设一个路段上有两个相邻的不同的交通流密度区域(k1和k2)，如图5-2所示，用垂直直线S分割这两种密度，称S为波阵面，设S速度为uω，A 段的车流平均速度为u1，密度为k1；B段的车流平均速度为u2，密度为k2，并规定交通流按照图5-2的x 正方向流动速度为正，反之为负。

由流量守恒可知，在时间t内通过界面S的车辆数N 可以表示为

整理可得：

由q=ku 可知：

代入式(5-19)得：

这里分为两种情况，交通波均向着与车流速度相反的方向传播，即uω＜0：

(1)q2＜q1且k2＞k1，波阵面经过之处车流密度增大，流速降低，称作集结波。

(2)q2＞q1且k2＜k1，波阵面经过之处车流密度减小，流速加快，称作消散波。

需要注意的是，将交通事故影响下交通波传播模型应用于道路全断面，得到的是各个车道的平均影响状况。

一般交通事故所诱发的交通波传播可分为四个过程：交通波三次集结和一次消散。第一个过程为事故发生后到拖挂车或警务车到场。在此过程中，由于事故发生占用一定数量的车道，事故点道路通行能力下降，车流开始拥挤。定义事故未影响到的车流状态为0状态，即发生前车流状态；事故发生后受到影响的车流状态为1状态。那么事故发生后产生的第一列集结波为ω01，向车流上游传播，其波速为(为了简化，此后将所有交通波波速uωij记为ωij)

第二个过程为事故处理阶段，从拖挂车或警务车抵达现场到事故处理完毕。在此过程中，事故点的道路通行能力进一步受到影响。定义此时车流状态为2状态，则第二列集结波ω12向上游传播，波速为

第三、第四个过程为交通恢复阶段，从事故处理结束到交通完全恢复。在第三个过程，事故车辆占用的车道被释放，事件点处道路通行能力得以恢复，交通消散波开始向上游传送。定义此时车流状态为3状态，消散波ω23的波速为

在第四个过程中，当ω23完全覆盖前两列集结波时，到达集结波影响的最远处。此后0状态与3状态相遇，q3＜q0且k3＜k0，则产生交通波ω03，且ω03＞0，即交通波向前传播使得车流逐渐向最初的0状态恢复。当ω03传播至事故发生点时，算作交通完全恢复。集结波ω03的波速为

由此，交通波传播速度基本模型为

式中 qi，qj——分别为状态i，j 的流量；

ki，kj——分别为状态i，j 的密度。

交通波传播速度模型中有流量和密度两个参数，而许多统计研究表明车流密度和速度之间存在一定的关系，通过q=ku 的转换关系可以将其转换为流量-密度关系，这样交通波传播速度模型中的流量可以被密度代换，进而实际检测数据中仅收集车流密度数据即可进行相关计算。

常用的速度-密度模型有：Greenshields线性模型、Greenberg模型和Underwood模型。(www.daowen.com)

(1)Greenshields模型：

式中 uf——自由流速度；

kjam——阻塞密度。

代入q=ku 可得

(2)Greenberg模型：

式中，um为流量最大时对应的车速，称为最佳车速。

代入q=ku 可得

(3)Underwood模型：

式中，km为流量最大时对应的密度，称为最佳密度。Underwood模型适用于密度较低的自由流。在研究交通偶发事件影响时，车流状况一般不为自由流，因此此处该模型不予考虑。

上述三个模型中，交通波理论较多使用的是Greenshields模型。为了便于推导，将密度进行标准化处理，令

式中，ηi为i车流状态的标准化密度，同式(5-28)一起代入式(5-26)可得

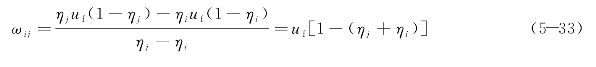
据此可以推导出传统的停车波模型和启动波模型。

假定车队以区间平均车速u1行驶，在交叉口停止线遇到红灯停车，此时k2=kjam即η2=1，有

当车辆启动时，k1=kjam即η1=1，且由于刚启动，车速u2=uf(1-η2)，相对于uf可以忽略不计，故有

对于传统的停车波和启动波模型，杨少辉等[4]在2008年利用北京城市快速路实际交通数据进行验证后发现，使用了Greenshields速度-密度关系的停车波模型与实际数据误差较大。其原因在于Greenshields模型本身有缺陷，不适用于描述交通流的拥挤状态和临界状态。而Greenberg速度-密度关系适用于交通流密度较大的拥挤状况。因此，在交通拥挤状况下使用Greenberg速度-密度关系对交通波传播速度模型进行修正，发现与实际数据拟合得较好。孙宇星等[5]通过北京城市快速路的多个检测器得到数据，拟合出了基于Eide分段指数模型的曲线，且其分段点密度分界值为25 pcu/km，当车流密度高于该分界值时，使用指数模型，相较于Greenshields模型误差明显减小。综合以上结论，为了更好地描述不同交通流密度状况下事件影响的交通波传播状况，我们针对不同密度的交通流相遇产生的交通波采用不同的速度-密度关系来标定其速度传播模型：以25 pcu/km 为界，以上算作高密度车流，对应使用Greenberg速度-密度模型；以下算作中低密度车流，对应使用Greenshields速度-密度模型。

将两种速度-密度模型，即式(5-28)和式(5-30)分别代入交通波速度基本公式，即式(5-26)，同样为了便于推导，对密度进行标准化处理，当高密度交通流与高密度交通流相遇产生交通波时有

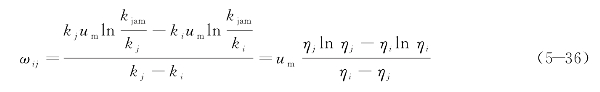
当高密度交通流与低密度交通流相遇时有

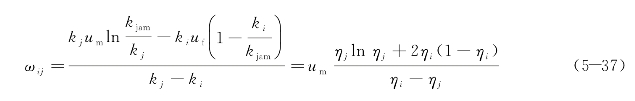
当两股中低密度交通流相遇产生交通波时，均使用Greenshields模型，则传播速度模型直接使用传统模型，见式(5-16)。