城市道路交通服务水平是根据通行能力和交通需求比较来评价的。当通行能力大于交通需求时，道路畅通；当通行能力小于交通需求时，道路上会发生交通拥堵。在交通需求一定的情况下，因道路养护作业而使道路通行能力降低导致了拥堵风险。因此，城市道路拥堵风险评估可从养护作业道路的通行能力计算入手。从1981年到现在，国内外提出的有关施工作业区通行能力的估计模型可分为以下五类。

1.函数模型

基本表达式：

式中 C——估计的通行能力，pcu/h；

C基——基本通行能力，pcu/h；

fi——影响因素修正系数。

1)C.Abrams和J.Wang模型[28]

C.Abrams和J.Wang是最初将施工作业区通行能力量化的研究者。他们考虑的因素是在1965年版HCM 的基础上(重型车、车道宽度、侧向净宽)增加了一个施工作业区因素，并将施工作业区的基本通行能力值定为2 000 vphpl(vphpl：vehicles per hour per lane，每小时每车道交通量)。

式中 TF——重型车修正系数；

WCF——车道宽度和侧向净宽修正系数；

WZF——此研究中确定的施工作业区通行能力修正值，vphpl。

2)R.A.Krammes和G.O.Lopez模型[14]

该模型估计的是短期施工作业区，引入一个新的基本通行能力值1 600 pcphpl(pcphpl：pcu per hour per lane，每小时每车道交通量)。模型包含了许多新因素，如工作活动类型、强度、匝道、开放车道数量等。该模型后来被HCM 2000引用。

式中 I——施工作业区作业类型、强度和位置的修正值，pcphpl；

R——匝道修正值，pcphpl；

fHV——重型车修正系数；

N——短期工作区内开放车道数。

3)A.F.Al-Kaisy和F.L.Hall模型[26]

此模型新考虑了天气状况和光线状况，还包括一个非加性相互作用效果的修正系数。A.F.Al-Kaisy和F.L.Hall指出驾驶人构成和重型车对通行能力的影响程度较大。

式中 fHV——重型车修正系数；

fd——驾驶人构成修正系数；

fw——工作强度修正系数；

fs——封闭车道位置(左或右)修正系数；

fr——雨天修正系数；

fl——光线条件修正系数；

fi——非加性相互作用效果的修正系数。

4)K.Heaslip模型[29]

K.Heaslip等人的研究分为两个阶段：一是仿真模型，使用CORSIM(Version 5.1)为各种不同的工作区场景建立一个综合的数据库，然后基于仿真数据和现有文献中的数据，提出了一个预测长期施工作业区通行能力的模型，考虑了三种施工作业区布设；二是用现场采集的数据来评估和改善分析模型。

式中 fl——光线条件修正系数；

fd——驾驶人构成修正系数；

fr——雨天修正系数；

Cunadj——不可调整的通行能力，vphpl；

VR——匝道交通量。

2.回归模型

1)J.L.Memmott和C.L.Dudek模型[30]

此模型增加了一个风险估计因子，具体见式(4-16)：

式中 CERF——通行能力估计风险因子；

a，b——研究中引入的两个系数。

2)T.Kim，D.J.Lovel和J.Paracha模型[16](www.daowen.com)

多元回归模型，基于2000年从12个施工作业区采集的现场数据，为车道位置和工作强度引入了哑变量；第一次考虑了重型车与坡度两个因素的联合作用对通行能力的影响。

式中 NUMCL——关闭车道数；

LOCCL——关闭车道的位置；

HV——重型车比例；

LD——施工作业区距开放车道的横向距离，km；

WL——施工作业区长度，km；

WIH——重工作强度；

WG——坡度。

3.经典宏观交通流模型

1)R.F.Benekohal行驶速度模型[31]

该模型认为工作强度、车道宽度和侧向净宽能够降低车辆速度。首先，计算工作区车辆的运行速度，然后基于流量-速度关系来计算流量。

式中 Uo——运行速度，mph^[1]；

FFS——自由流速度；

Rwi——工作强度引起的速度的减少；

Rlw——车道宽度引起的速度的减少；

Rlc——侧向净宽引起的速度的减少；

Ro——其他因素引起的速度的减少。

2)W.A.Sarasua模型[20]

使用宏观交通流的典型方法分析交通特性，基于速度-密度的线性关系假设，推导出流-速-密和车头时距的关系。

式中 Cb——基本通行能力；

I——工作活动类型、强度，施工作业区长度和位置的修正系数；

fHV——重型车修正系数；

N——开放车道数。

3)H.Ramezani模型[32]

H.Ramezani等[32]提出了三种估计施工作业区通行能力的方法。

第一种是h-n模型。该模型是对车头时距的优化。在交通流没有达到饱和时，最大15 min流率低估了其通行能力。把这个15 min分为两部分：充分利用时间和未充分利用时间。用充分利用时间来计算流率。

第二种是基于所有在排车辆的模型。

式中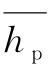， 是所有在排车辆的平均车头时距。

第三种是基于中长排队情况的模型。

式中， 是在排车辆超过四辆的车队的平均车头时距。

4.神经网络模型

1)A.Karim 和H.Adeli模型[33]

他们提出了一种自适应计算模型来估计施工作业区的通行能力、排队长度和延误，考虑了11种因素：车道数、开放车道数、施工作业区布局、施工作业区长度、车道宽度、重型车比例、坡度、速度、工作强度、黑暗因素和临近匝道。该模型集合了交通流理论的数学严谨性和神经网络分析的自适应性。径向基功能神经网络模型从影响因素学习映射，对通行能力进行估计。排队长度和延误是在通行能力的基础上使用交通流模型得到的。

2)H.F.Adeli和F.ASCE模型[21]

H.F.Adeli等提出一种新型的模糊神经逻辑模型来估计施工作业区的通行能力，在A.Karim 的基础上将黑暗因素进行了展开：施工作业区位置、施工作业区持续时间、测量时间、测量日期、天气状况、路面状况、驾驶人构成。该模型具有良好的泛化性能，当只有部分数据可得时，表现出很强的优越性。有助于开发智能决策系统来进行场景分析，从而制定交通管理计划。

5.分类均值模型

J.Weng等[34]基于决策树模型考虑了16种影响因素，从现有文献和实地采集了182组数据，分为三个部分：训练数据、核查数据和评估数据。他们将训练数据根据施工作业区场景的特征进行分类，划分方法是决策树方法，使得每一类数据之间的差异性最大。最终得到了一棵最大树深是16，叶子数也是16的最佳生成树。每个叶子节点对应一个通行能力值，取值是每组数据的平均值。该模型对长期和短期施工作业区都适用。