城市交通与公路交通既有相似之处，也有许多不同的特征。由于公路和城市道路所处位置不同，所服务的人群不一样，提供的功能也有所差异，因而公路交通流与城市交通流就存在着不同的特征。从驾驶人组成来看，在公路上专业司机较多，而在城市中尤其是大城市，私家车占了一定的比例，私家车的驾驶人一般来说本身即是车主，还拥有其他的工作，从驾车技术方面来说，与职业驾驶人有一定的差别。从车辆组成来看，城市道路上多为小客车，而公路上货车所占比例较大。因此，城市交通流车辆换算时以小客车为标准车，公路交通流车辆换算时一般以货车为标准车。由于不同类型的机动车动力性能不同，有时甚至差别很大，因此不同的交通组成必然会反映出不同机动车的性能特点，使得公路与城市道路上的交通流有一些差别。

另外，在城市道路系统中，由于交通流运行过程中受到信号灯的周期性阻滞作用，所以交通流具有典型的时变性、非线性和间断性特点[9]。城市道路上大量平面交叉口的存在，使得交通流受相交道路车流或信号灯控制的影响非常大[10]。所以，若按照交通设施对交通流的影响来划分的话，交通流可以分为非间断交通流(或称连续交通流)和间断交通流。城市道路(除快速路外)多属于间断流设施，因为存在很多信号控制交叉口，车辆不能连续地行驶，往往走走停停。由于城市道路交通流存在间断性这一特点，除了速度、流量与密度等宏观交通流特征外，行程时间也常被用来表征城市道路的拥堵状况。

1.自由流车速分布

自由流车速是交通流理论中一个很重要的参数，它具有相对的稳定性。自由流车速不仅是对连续流进行通行能力研究和道路服务水平分析的基础，同样对于承载间断交通流的城市干道交通功能的研究也具有重要意义。在HCM2016中，自由流速度是指给定的交通设施在低交通量情况下的车辆平均速度，此刻驾驶人按照期望速度行驶，且不受控制延误的影响。基于这样的定义，本节研究的城市道路自由流车速是指不受交叉口排队、进出交通等因素影响的自由行驶车辆的速度，其主要取决于道路条件、车辆性能、驾驶人行为特性等。在忽略车辆性能、驾驶人等因素的影响下，通过采集城市干道上足够多的自由流车速样本并进行分析，以反映城市道路的功能、质量和服务水平[11]。

1)车速分布拟合方法——Kolmogorov-Smirnov检验

Kolmogorov-Smirnov检验(K-S检验)基于累积分布函数，用以检验某个经验分布是否符合某种理论分布或比较两个经验分布是否有显著性差异。单样本的K-S检验是用来检验一个数据的观测经验分布是否是已知的理论分布。当二者间的差距很小时，推断该样本取自已知的理论分布。作为零假设的理论分布一般是一维连续分布F(如正态分布、均匀分布、指数分布等)，有时也用于离散分布(如泊松分布)，即H0：总体X 服从某种一维连续分布F。

检验统计量为

H0真，Z 依分布收敛于Kolmogorov分布，即当样本取自一维连续分布F 时，

当F 是连续分布时，随机变量K 的分布不依赖于F。

2)实例分析

选取2012年上海市城市次干道自由流车速的调查数据进行分析。在天气状况良好的条件下，在北京西路上选择车流密度小，且不受下游车流影响的两个路段，于22∶00后进行自由流车速的调查。

将调查所得的107个样本数据按照5 km/h的组间距进行分组，计算组中值，统计各组频数，并计算频率，结果见表2-1，绘制的自由流车速频数分布直方图如图2-4所示。

表2-1　车辆速度分布统计表［11］

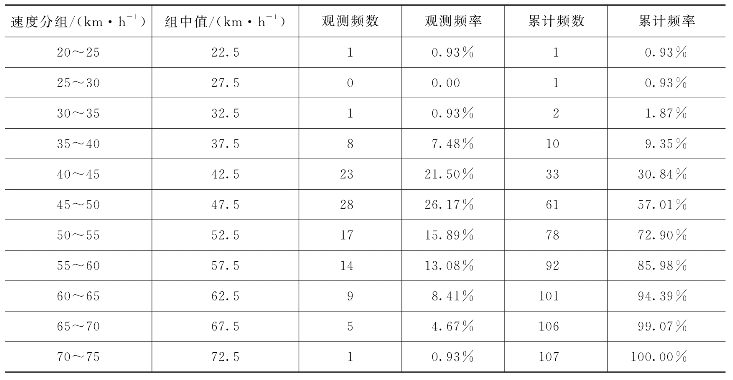
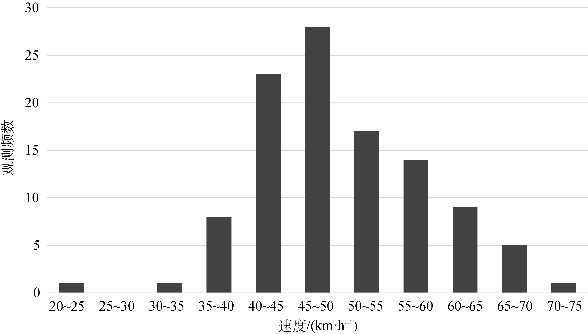
图2-4　自由流车速频数分布直方图

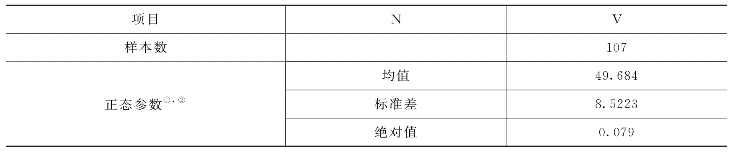
根据K-S检验原理，检验结果见表2-2。

表2-2　单样本K-S 检验

(续表)

注：①检验分布为正态分布。
②根据数据计算得到。

由表2-2可以看出，参与检验的样本数有107个，双尾检验计算得到显著水平P=0.525，取显著水平α=0.05，P ≫α，说明该组自由流车速服从正态分布。

2.基本图模型

1)Van Aerde模型

Van Aerde模型为传统路段交通流基本图模型之一。1995年，Michel Van Aerde推导了经典的四参数单一结构连续模型。该模型具体公式为

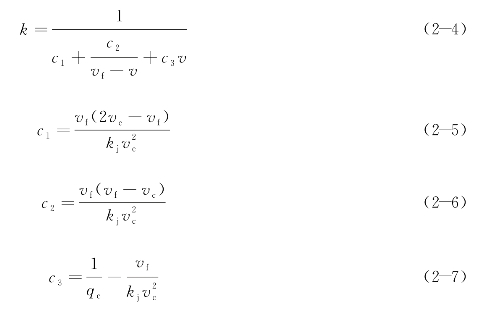
式中 k——交通流密度，pcu/km；

v——交通流速度，km/h；

qc——通行能力，pcu/h；

vf——自由流速度，km/h；

vc——临界速度，km/h；

kj——阻塞密度，pcu/km；(www.daowen.com)

c1，c2，c3——模型的三个中间变量。

交通量的特征参数(通行能力qc、自由流速度vf、阻塞密度kj和临界速度vc)是Van Aerde单一结构模型的基础，可用于计算c1，c2，c3。Van Aerde模型的关系曲线形式如图2-5所示。

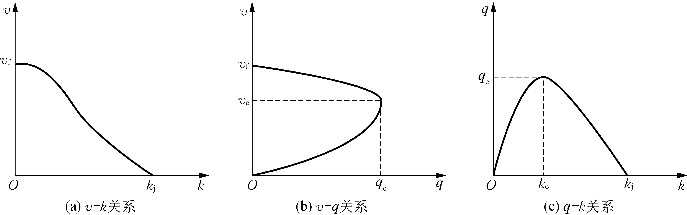
图2-5　Van Aerde模型关系曲线

Van Aerde单一结构模型较为简单，易于标定。常用的其他交通流基本图模型，如Greenshields模型和Pipes模型是其特殊形式。

建立交通流模型的基本方法有两种[12]：

(1)通过理论分析建立理论模型，即通过对交通流进行机理分析以确定关系模型，再利用实测数据来标定模型参数。这种方法有较强的理论支撑，但是由于实际道路条件、交通条件差别很大，交通流的随机性又比较强，参数间的关系复杂，根据经典的理论模型，难以标定其中的参数。

(2)根据实测数据建立经验模型，近年来的交通流模型大多基于实测数据建立。由实测数据直接分析得到的交通流模型与数据的拟合度较高，但是由于经验性太强，没有比较完善的理论说明。

以上两种方法各有利弊，为了扬长避短，可先根据实测数据的分布建立模型，但在建模的同时须遵循基本的交通流理论。因此，首先根据实测交通参数关系图确定所选择模型的大体形态；其次，利用多个经典交通流模型拟合选定最优的模型形式。

2)实例分析

(1)相关参数标定

为了研究城市道路交通流基本图模型，至少需要收集速度、密度、流量三类数据中的两类，然后还需要进行自由流速度、通行能力和临界速度的标定。依托北京市交通信息采集系统以及流量调查，获取2013年北辛安路(次干路)速度和流量数据。

对基于Van Aerde模型所获取的流量与速度数据呈现出来的交通流特征参数(自由流速度、通行能力、临界速度)进行标定，模型标定特征参数值如表2-3所列。

表2-3　基于RTMS数据和FCD的参数标定结果

注：①数据来源于远程交通微波传感器。
②数据来源于浮动车。

通过对表2-3进行分析，可以有如下发现：

①对于检测路段一，基于RTMS的自由流速度达到70 km/h、临界速度达到51 km/h，高于基于FCD 的自由流速度值66 km/h和临界速度值36 km/h。

②对于检测路段二，基于RTMS的自由流速度达到76 km/h、临界速度达到61 km/h，高于基于FCD 的自由流速度值66 km/h和临界速度值43 km/h。

以上两个现象是基于RTMS的速度为时间平均速度，基于FCD 的速度为空间平均速度。而在干扰因素较多的城市道路上，时间平均速度更是明显高于空间平均速度，HCM2016中也提到：在同一场景下，时间平均速度总是高于空间平均速度。

另外，在两个检测路段上，FCD 速度随流量的增大导致的下降快于RTMS速度，这是因为FCD 速度为平均行程速度，能够体现路段内车辆与车辆之间的相互干扰。

(2)模型拟合

分别利用线性模型、对数模型和指数模型对平均速度与平均密度散点图进行拟合，拟合结果如表2-4所列。

表2-4　平均速度与平均密度关系的三种模型拟合结果①

注：①岳园圆：《基于多源数据的北京市多层次交通流基本图研究》，硕士学位论文，北京交通大学，2015年。

单从三个模型曲线拟合的判断系数来看，R 2 都大于0.90，尤其是线性模型和指数模型，R 2均达到0.98以上，相比较而言，对数模型与实际数据的偏离较大。另外，线性模型在中密度时，略高于实测数据，在高密度时又略低于实测数据；指数模型在低、中、高密度时均能较好拟合实测数据。根据以上分析，最终选择适用于小密度状态下的Underwood指数模型作为平均速度与平均密度模型，模型表达式为

式中 vf——自由流速度，km/h；

km——最佳密度，pcu/km。

根据q=vk，推导平均流量-平均密度关系模型和平均流量-平均速度关系模型，分别为

根据以上模型，对次干路交通流三参数基本图进行拟合，得到基本图模型为