I.4.1 平稳随机过程的相关函数与功率谱密度函数的解

3.4节阐述了地震作为随机过程的振动反应，并详细推导了地面输入为随机白噪声S0时单自由度平稳过程的解，其结果如下：

（1）输出相对位移（yt）、相对速度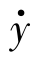t）和绝对加速度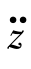t）的相关函数的解为

式中，ω0，ξ分别为单自由度系统的固有圆频率和阻尼比。

（2）输出对应的均方值。

将τ=0代入Ryy（τ），Ry·y·（τ）与）可得到相对位移y（t）、相对速度与绝对加速度的均方值。

（3）输出相对位移y（t）和绝对加速度的功率谱密度函数为

式中，ω0为单自由度系统的固有圆频率，ω为圆频率成分，ξ为单自由度系统的阻尼比，为单自由度系统基础输入加速度功率谱密度函数。

I.4.2 平稳随机过程的谱参数求解

设式（I.26）中为平稳随机过程白噪声功率谱密度函数，将（I.26）的输出相对位移y（t）的功率谱密度函数Syy（ω）代入式（I.5）后得

令无量纲u=ω/ω0，代入式（I.27）得

设

将式（I.29）代入式（I.28）得

另外可明显得到λ0和λ2为

将λ0，λ1和λ2代入式（I.11）得形状系数q为

当ξ很小时可近似得到q与成正比的参数。

I.4.3 非平稳随机过程的相关函数与功率谱密度函数的解

仍设输入在t=0时突加一个白噪声S0的阶跃函数，非平稳随机过程反应y（t）自相关函数的解为，

式中，t1，t2是非平稳随机过程中两个时间点，p=Ryy（τ）是由式（I.22）中给出的平稳随机过程反应y（t）的自相关函数，同理可得(www.daowen.com)

根据上式，也可得到y（t）和均方差为

式中，

该两值是平稳随机过程输出y（t）和的均方值。从式（I.34）、式（I.35）可清楚看出，当t1，t2→∞时，其相关函数的反应趋向于平稳随机过程的解。

图I.2是以ω0t为无因次横坐标画出无因次反应y（t）对应不同阻尼比的方差值ψ2［y（t），t］之间的关系曲线，从图中可清楚看出，从非平稳过渡振动转移到平稳反应时，阻尼比ξ越大，其过渡时间越快趋近于平稳随机过程。

图I.2　单自由度系统对白噪声激励的位移反应均方差

将式（I.34）Ryy（t1，t2）代入式（I.18）并积分后可得到反应功率谱密度函数Gyy（ω，t）为

式中，p= ω0，ω0和ξ为单自由度系统固有圆频率与阻尼比，ω为功率谱密度Gyy（ω），的频率成分，H（jω）为单自由度系统的传递函数。

I.4.4 非平稳随机过程的谱参数求解

利用式（I.38）代入式（I.20）对ω积分后求得λ0（t）为

这与式（I.36）的ψ2［y（t），t］的结果相对应，当系统阻尼比很小ξ≤0.10时，式（I.41）可近似变为

同理可求得近似解为

式中，ωu为输入函数中圆频率ω成分的上限值。

去除式中发散项后的结果可表示为

将式（I.44）代入式（I.8）后得到非平稳随机过程下功率谱密度函数的形状扩展系数为

由式（I.45）可清楚看出形状扩展系数q（t）是ω0和阻尼比ξ的函数，图I.3显示，不同阻尼比ξ=0.10，0.01，0.001时，q（t）随着ω0t的增大而同步减小，也就说明反应y（t）（或）从宽频带随机过程逐步转变为窄频带随机过程，即逐步变成为接近固有圆频率ω0的窄带共振过程。

图I.3　反应y（t）的Gyy（ω，t）形状扩展系数q（t）变化

当时间t→∞时，式（I.44）和式（I.45）得到的是平稳随机过程下的功率谱参数λ0，λ1，λ2和q。