设一随机时程x（t）的平均值为零，且是平稳的随机过程，在第2章中所定义的双边功率谱密度（PSD）函数为S（ω），与对应的自相关函数之间成傅里叶变换与反变换关系。

通常采用定义为正域（ω≥0）内的单边PSD函数G（ω），把G（ω）=2S（ω）关系代入式（I.1）得

式（I.2）中自相关函数R（τ）取τ=0，则等于x（t）的均方值。

为此，定义G（ω）的积矩为

当取k=0，1和2时分别为

λ0是表示G（ω）所包含的全部面积，等于x（t）的均方值ψ2［x（t）］，ω1则是G（ω）的面积距离原点ω=0处的重心矩，ω2为G（ω）的面积对于原点ω=0的回转半径。

再引入表征G（ω）形状扩展程度的无量纲参数：

对每一个谱矩存在一个特征频率ωk，表征为

这些特征频率形成一个有序的数列ωk≤ωk+1（k=0，1，2，…），表征其特征时，将ω1称为平均频率，ω2称为均方根频率，而ωs称为标准差频率，定义为

式（I.6）则可表示为

根据施瓦兹不等式可知(www.daowen.com)

即满足0≤q≤1。

这里参数q的物理意义为：如果G（ω）只在1个圆频率ω0处有峰值，而在其他圆频率ω处为0时，即表征为一个正弦波，则G（ω）=δ（ω-ω0），式（I.10）变为=1，代入式（I.9）得q=0。由此可看出，当q取小值接近于0时，x（t）表征为一个窄带噪声的随机过程，反之取q=0.35～1较大值时，x（t）变为一个宽带噪声的随机过程，所以通常将q称为PSD的形状系数。将式（I.9）变为式（I.10）变为

如果将G（ω）用面积作G（ω，t）dω归一化处理，且将G（ω）/λ0模拟为ω的概率密度函数时，则ωs可视为是ω的标准偏差比。同理，由图I.1所示，ω1可视为G（ω）在频域ω上的平均值，ω22可视为是G（ω）在频域上的均方值，ωs则可认为是G（ω）对于ω1的回转半径。

图I.1　谱参数物理意义

而

也可视为G（ω）的形状参数，ωs/ω1为G（ω）/λ0的变化系数。上述参数作为时间域内的物理意义又有以下关系。

（1）λ0=ψ2［x（t）］，即x（t）平均值为0的均方差值。

（2）λ2=∫∞0 ω2G（ω）dω=ψ2［x·（t）］，即x·（t）平均值为0的均方差值。

（3）ω2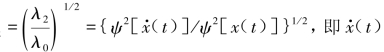和x（t）的标准偏差比值。