H.3.1 随机振动过程PSD定义的不同格式

随机振动过程的PSD在数学上定义为自相关函数的傅里叶变换，因此对给定的随机振动过程在应用不同的傅里叶变换格式时，能获得不同的PSD估计公式。对应式（H.18）～式（H.20）格式，所得到PSD与自相关函数R（τ）之间的关系分别定义为下列的3种不同的格式：

其傅里叶反变换得到R（τ）为

式中，S（ω）为双边功率谱密度函数；ω为圆频率；R（τ）=E［x（t）x（t+τ）］为随机函数x（t）的自相关函数，E［x（t）x（t+τ）］为x（t）x（t+τ）的期望值，E［x（t）x（t+τ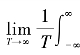）］=x（t）x（t+τ）dt。

对于离散化数据处理方法，PSD的估计公式也有典型的不同形式离散公式：

式中，k，r分别为频域和时域上的离散数，xr为时程x（t）用离散时间r表征的幅值。

可见，不同的傅里叶变换格式会产生不统一的双边功率谱密度函数S（ω）估计结果，在核电厂抗震设计与振动分析中，PSD作为描述随机过程强度的统计参数之一，会造成分析结果出现严重的偏差。

H.3.2 随机振动中PSD的物理定义

从国内外有关资料或标准可知，在随机振动领域中PSD的物理定义正如2.4.4节中所述，单边自功率谱函数G（f）定义为随机信号数据x（t）通过中心频率为f、带宽为Δf的窄带滤波器后，获得时间历程x（t，f，Δf）的均方值，当带宽Δf趋向于零，平均周期T趋向无穷大时，其均方值ψ2（f，Δf）的极限称为随机信号x（t）的单边功率谱密度函数（PSD），其数学表达式为

G（f）为单边功率谱密度函数，对应式（H.22）中的双边功率谱密度函数S（ω）存在关系：

式中，ω=2πf。

H.3.3 PSD不同计算格式与相关函数R（τ）之间关系的解析

对于任意实随机信号函数x（t），在有限周期T范围内的平均功率，（即x（t）的均方值ψ2）可表示为

（1）若x（t）的傅里叶变换式设为X（ω），由于X（ω）有不同的变换格式，取式（H.18）格式代入式（H.27）进行分析。

应用傅里叶变换的时移定理性质可知

代入式（H.28）后可得

（2）同理，取式（H.19）格式代入式（H.27）进行分析。

而时移定理形式变为(www.daowen.com)

代入式（H.31）后可得到

（3）同理，取式（H.20）格式代入式（H.27）进行分析。

而时移定理形式变为

代入式（H.35）后可得

（4）对傅里叶变换3种不同格式作比较后得到结果式（H.30）、式（H.33）和式（H.36）3个等式，可清楚看出，分别比较等式两边后均可得到下述关系式：

应用式（H.26）关系式，对应单边功率谱密度函数G（f）可表示为

也就是说，无论采用哪种傅里叶变换格式，对应功率谱密度函数S（ω）［或G（f）］与相关函数R（τ）之间的傅里叶变换关系是唯一的。

（5）如果假定傅里叶变换的基本格式的通用形式与时移定理形式可表示为

当m分别取1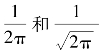，时，可与式（H.18）～式（H.20）3种变换格式相对应。

将式（H.39）代入式（H.28）后，得

由此可见，同样可获得式（H.37）和式（H.38）的结果，也就是说，无论采用何种傅里叶变换格式，PSD函数与自相关函数R（τ）之间的关系是唯一的。说明在式（H.22）中第一个表达式S（ω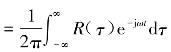）才是正确无误的。

H.3.4 PSD不同计算格式与随机信号x（t）之间关系的解析

同理，将式（H.39）代入式（H.28）后可得

比较两边并再利用（H.39）中反变换可得到S（ω）：

从式（H.42）也可清楚看出，无论采用哪一种傅里叶变换格式，其得到的PSD与信号x（t）之间关系的结果也是唯一的。但要特别引起注意的是，因x（t）与X（ω）之间傅里叶变换格式并不是唯一的，则S（ω）与X（ω）的关系也存在3种不同的表达式。

对于G（f）的离散形式应为

式中，h为信号x（t）的离散后等时间间隔。