傅里叶变换的原始概念是从周期性函数展开为三角级数演变而来，如果一个以T为周期的函数x（t）在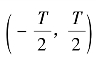）上满足狄利克雷条件，即

（1）除去有限个第一类间断点处，处处连续。

（2）分段是单调，且单调区间的个数有限。

则x（t）的傅里叶级数可用近似表达式记为

若在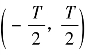上处处收敛，且在xT（t）的连续点处级数式（H.1）收敛于x（t），其中

设xT（t）在时程t上均值为零时，则式（H.3）中a0≡0。为了求解方便，常利用欧拉公式：

将xT（t）的傅里叶级数改写为复数形式，将式（H.4）代入式（H.3）后，则式（H.1）式的xT（t）变为

则得到xT（t）可用傅里叶级数的指数形式表示为

这里系数Ck对应ak和bk用（H.3）代入得

可以合成为一个表达式为

将式（H.9）代入式（H.7）后得

如设函数x（t）在实轴上处处有定义，如x（t）在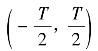区间的一部分独立出来，并按周期T向左和向右拓展所获得的x（t）如图H.1所示，如记x（t）所形成的周期函数为xT（t）。当T越大，则xT（t）与x（t）相等的范围则越大。当T→∞时，则以T为周期的函数xT（t）的极限值转化为x（t），即

也说明任何一个非周期函数x（t）均可看成以T为周期的函数xT（t）时，取T→∞条件下转化而来的。利用式（H.10）和式（H.11），得

图H.1　xT（t）与x（t）函数之间的关系

如果记XT（ωk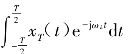）=(www.daowen.com)

则式（H.12）变为

图H.2　频率域ω上的频率分割

式（H.13）中，当k取正整数时，ωk所对应的点认为均匀分布在整个频率轴ω上，如图H.2所示。

若频率域ω上相邻两个点之间的距离以Δωk表示，即

Δωk=ωk-ωk-1=kω-（k-1）ω=ω=2π/T

（H.14）

将T=2π/Δωk代入式（H.13），则

当T越大时，Δωk就越小，当T→∞时，Δωk→0，这时可以在ω轴上直接用连续变量ω来代替离散变量Δωk，记X（ω）为

将式（H.16）代入式（H.15），则可转换成在整个频域［-∞，∞］上的广义积分，记为

记式（H.17）为傅里叶变换的基本格式时，X（ω）称为x（t）的傅里叶正变换，式（H.17）中的x（t）则称为X（ω）的傅里叶逆变换。

如将式（H.17）的变换记为第二种格式时可以表示为

则按同样的方法，可推出其他两种常见的（第一种和第三种）傅里叶格式为

可清楚地看出对于一种时程x（t），可以得到3种不同的傅里叶变换格式X（ω），对X1（ω），X2（ω）和X3（ω）表达式之间的数值关系为

式（H.18）～式（H.20）是傅里叶变换的3种基本格式，对数学上应用也许不存在什么问题，但是应用到振动或地震分析领域中，将会引起随机过程中的PSD估计产生非唯一性问题，出现此现象可作如下的解析。