G.4.1 参数

一端固定的悬臂梁，上部自由端处有一个单向间隙元（见图G.2），间隙元刚度为KG，梁上与间隙元之间接触处的碰撞刚度为Ki，其参数如表G.1所示。

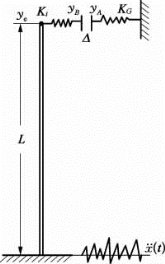
图G.2　考题模型

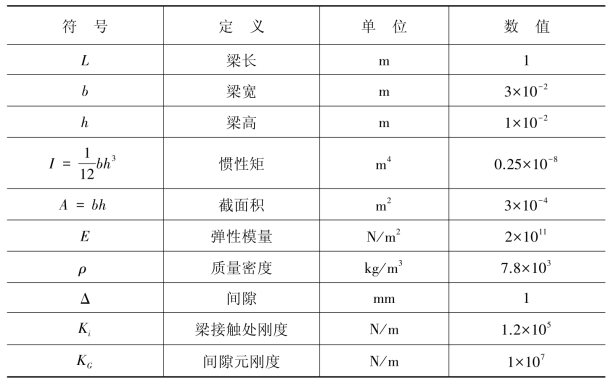
表G.1　参数表

作用在梁基础固定处的地震水平加速度时程设为一个正弦脉冲时程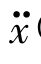t）为

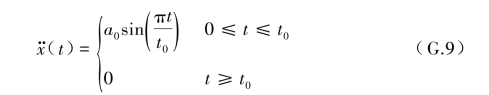
梁的初始t=0时y0==0

G.4.2 模态特征值

梁的固有圆频率ωj与振型函数φj可查表5.5.2中一端固定一端自由边界条件的数据。其梁的固有圆频率ωj和固有频率fj为

其梁的模态振型为

φj=Bjsin λjx+Cjcos λjx+Djshλjx+Echλjx

（G.11）

将表G.1所列梁的参数代入式（G.10）和式（G.11），并参照表5.5.2计算前4阶振型的结果如表G.2所示。

表G.2　梁的特征值与振型常数值

G.4.3 模态叠加法计算结果(www.daowen.com)

为了比较模态叠加法与直接积分法的计算结果，该考题应用ANSYS大型结构分析程序中梁单元和碰撞间隙单元进行计算。其参数均用表G.1所列数据代入，模态叠加法所计算的固有频率与振型均与表G.2所列理论解析解十分接近。两种方法采用时间积分步长Δt取10-6 s，模态截止频率取400 Hz时可满足式（G.8）的收敛条件。

两种方法的最大位移和间隙处碰撞力最大峰值如表G.3所示。

表G.3　两种方法计算结果比较

梁自由端水平位移、速度yi和间隙处碰撞力FG的时间历程曲线图分别如图G.3～图G.5所示。

图G.3　梁自由端处位移y（t）

（a）模态叠加法；（b）时间历程法

图G.4　梁自由端处的速度（t）

（a）模态叠加法；（b）时间历程法

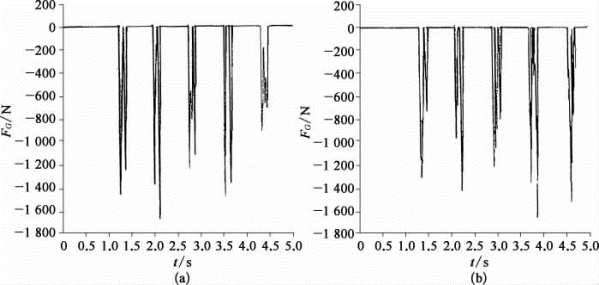
图G.5　间隙元处的碰撞力FG（t）

（a）模态叠加法；（b）时间历程法

从表G.3和图G.3～图G.5所示曲线可清楚看出：

（1）两种方法计算结果的规律和数值十分相近。

（2）梁自由端处由于单向间隙元的刚度十分大，在间隙元方向上的运动受阻使其位移量十分小，而反方向由于无阻碍为自由运动，造成梁自由端水平位移基本上为单向运动波形。

（3）由于间隙元处的碰撞刚度KG十分大，同时梁自由端位移运动受阻而产生一个高频多次接触回弹的脉冲撞击力波形。

（4）从两种方法所耗时CPU运算时间可看出，其模态叠加法比直接积分法的总运算时间要少一个量级。