E.3.1 考题1——等频变幅（1）

该考题是主频f0不变而振幅有周期变化，其频谱图除主频f0外，还会出现低于或高于主频f0的其他周期性频率成分（k=1，3，5，…）的信息。验证加速度、速度和位移谱值ak和bk是否正确，以考核积分程序的正确性。以3个不同主频f0作为考题，该类型加速度波形在FFT变换中特别注意低频滤波的范围，防止失去最低频率对位移幅值的贡献。

加速度时程（见图E.1）为

式中，

图E.1　加速度时程

由式（E.12）可得

将式（E.1）中用ωk=kω代入后得到

其系数ak和bk为

将式（E.11）的a（t）代入式（E.15）后并运用式（E.12）和式（E.13），经运算后可得ak和bk为

代入式（E.9）得到速度为

代入式（E.10）得到位移为

如已知：A=10 m/s2，f0=2 Hz，T=1 s，f=1 Hz，n=f0/f=2，m=0.5。

可按式（E.14）～式（E.18）求得加速度、速度和位移上各阶频率fk对应的系数幅值，如表E.1所示，其主频为f0=2 Hz的幅值为b2。

表E.1　各阶频率对应加速度、速度和位移的系数幅值

表E.1中，主频f2=2 Hz时，其低频f1=1 Hz对位移d1的贡献是主要的成分，所以需注意对最低频率滤波值的控制。

E.3.2 考题2——等频变幅（2）

同E.3.1中考题1，其参数改变为

A=10 m/s2，f0=10 Hz，T=1 s，f=1 Hz，n=f0/f=10，m=0.5。

其结果如表E.2所示，其主频为f0=10 Hz的幅值为b10。

表E.2　各阶频率对应加速度、速度和位移的系数幅值

表E.2中，主频f10=10 Hz时，其低频f1=1 Hz对位移d1的贡献比d10高得多，而成为最主要的成分，所以需注意对最低频率滤波值的控制。

E.3.3 考题3——等频变幅（3）

同E.3.1中考题1，其参数改变为

A=10 m/s2，f0=20 Hz，T=1 s，f=1 Hz，n=f0/f=20，m=0.5。

其结果如表E.3所示，其主频为f0=20 Hz的幅值为b20。

表E.3　各阶频率对应加速度、速度和位移的系数幅值

（续表）

表E.3中，主频f20=20 Hz时，其低频f1=1 Hz对位移d1的贡献比d20高一个量级，而成为最主要的成分，所以需特别注意对最低频率滤波值的控制。

E.3.4 考题4——具有真实低频成分的信号

对于两频率十分接近的正弦波（或余弦波）相乘后，会出现极低频与高频的波形相叠加（见图E.2）。其频谱图上极低频率上幅值对速度与位移的影响将成为主要的。所以要特别注意对极低频率滤波的范围，防止失去主要低频位移的幅值。

图E.2　加速度时程

加速度时程为

式中，ω1=2πf1，ω2=2πf2。

如：A=10 m/s2，f1=20 Hz，f2=20.5 Hz。

代入式（E.19）得

a（t）=5［cos 2π（0.5）t-cos 2π（40.5）t］

v（t）=+1.591 5sin 2π（0.5）t-0.019 65sin 2π（40.5）t

d（t）=-0.506 6cos 2π（0.5）t+7.721 5×10-5cos 2π（40.5）

其结果如表E.4所示。

表E.4　各阶频率对应加速度、速度和位移的系数幅值

E.3.5 考题5——相近频率的分辨能力

对于两频率十分接近的正弦波（或余弦波）相加后，会出现极低频率的拍波（见图E.3）。其频谱图上呈现十分接近的两频率的幅值图。该考题主要考虑两个十分接近频率之间的频率成分和幅值是否能被分辨出来。

加速度时程为

式中，ω1=2πf1，ω2=2πf2。

图E.3　加速度时程

如：A=10 m/s2，f1=20 Hz，f2=20.5 Hz。

代入式（E.20）得

a（t）=10［sin 2π（20）t+sin 2π（20.5）t］

v（t）=-0.079 58cos 2π（20）t-0.077 64cos 2π（20.5）t

d（t）=-6.332 6×10-4sin 2π（20）t-6.027 74×10-4sin 2π（20.5）其结果如表E.5所示。

表E.5　各阶频率对应加速度、速度和位移的系数幅值

E.3.6 考题6——多频谱矩形波

矩形波是无限个正弦（或余弦）波的谐波的组合，该考题考核主频f0（k=1）以及高阶（kf0）频率（k=3，5，7，…）对应的幅值精度。特别要注意对矩形波进行FFT后，防止频率混淆所产生低频成分的渗入。

加速度时程为

图E.4　加速度时程

按式（E.14）、式（E.15）展开成傅氏级数：

其傅里叶系数为

式中，ω0=2πf0，k=1，3，5，…

如：A=10 m/s2，f0=20 Hz，T=1/f0=0.05 s，代入式（E.23）求得其结果如表E.6所示。

表E.6　各阶频率对应加速度、速度和位移幅值

E.3.7 考题7——平均值不为零

该考题是平均值不为零的正弦波曲线展开为傅里叶级数后将出现刚体运动的系数项，对于该类时程必须预先做低频的滤波处理，将刚体运动时程去除，或预先将加速度时程（见图E.5）平均化处理，以确保得到的曲线是正确的。

图E.5　加速度时程

加速度时程为

a（t）=A|sin ω0t| 0≤t≤T

（E.24）(www.daowen.com)

按式（E.14）、式（E.15）展开成的傅氏级数为：

其中第一项平均值不为零，表征加速度为常数的刚体运动，在交变时程信号中可以将基频2f0以下的低频部分滤去。其傅里叶系数为

式中，ω0=2πf0，k=1，3，5，…

如：A=10 m/s2，f0=20 Hz，T=1/f0=0.05 s，代入式（E.26）求得其结果如表E.7所示。

表E.7　各阶频率对应加速度、速度和位移幅值

E.3.8 考题8——等幅变频

该题是与E.3.1等频变幅相反的等幅变频考题（见图E.6）。其频谱图上除两个主频f1和f2外，还会出现低于或高于主频f1，f2的其他频率成分的信息。验证加速度、速度和位移谱值ak和bk是否正确，以考核积分程序的正确性。该类型加速度波形在FFT变换中应特别注意低频滤波的范围，防止失去最低频率对位移幅值的贡献。

图E.6　加速度时程

加速度时程为

式中，

按式（E.14）、式（E.15）展开成傅氏级数的系数为

加速度、速度与位移分别由式（E.14）、式（E.17）和式（E.18）计算。

如：A=10 m/s2，f=1 Hz，T=1 s，f1=10 Hz，f2=20 Hz，n1=f1/f=10，n2=f2/f=20，代入式（E.29）整理后得到

求得结果如表E.8所示。其中主频为f10=10 Hz和f20=20 Hz的幅值为b10和b20。

表E.8　各阶频率对应加速度、速度和位移幅值

（续表）

表E.8中，主频f10=10 Hz和f20=20 Hz时，其低频f1=1 Hz对位移d1的贡献比d10和d20高得多，d2的贡献与d10和d20达同一量级。所以需特别注意对最低频率滤波值的控制。

E.3.9 考题9——等幅扫频（1）

等幅扫频波是频率随时间按一定规律变化的等幅正弦波（余弦波），虽按式（E.1）～式（E.5）不能得出理论解，但可以求得数值解，再按式（E.9）和式（E.10）求得速度和位移。频谱在包含扫频范围内的频率成分外，还要注意扫频周期T对频率成分的影响，如果T十分短，则扫频时程趋向于带宽的白噪声。这里列举3个不同扫频频宽的例子，以供相互比较。

加速度时程为

a（t）=Asin ωt 0≤t≤T

（E.31）

式中，ω=2πf；f=f0×10αt，为随时间t变化的扫频频率；t为时间；T为扫频一次的周期；α为扫频速率，是一个定常数；f0为扫频的起始频率，fn为扫频的结束频率。

对f=f0×10αt取10为底的对数变成

按式（E.32）可得结束时间tn，即等于扫描周期T。

如α=1 s-1时其扫频为1/3倍频程递增的速率，即两个相隔频率比为fi/fi-1=21/3≈101/10，其对数为如：f0=10 Hz，T=1 s，fn=100 Hz的扫频间隔如表E.9所示。

lg（fi/fi-1）=lg 21/3≈0.1

（E.34）

表E.9　10～100 Hz扫频频率与时间的关系

加速度扫频时程如图E.7所示。

E.3.10 考题10——等幅扫频（2）

同E.3.9中考题9的式（E.31）～式（E.33），其参数改变为

A=10 m/s2，α=2 s-1，T=1 s，f0=1 Hz，fn=100 Hz

如已知：A=10 m/s2，α=1 s-1，T=1 s，f0=10 Hz，fn=100 Hz。

加速度扫频时程如图E.8所示。

E.3.11 考题11——等幅扫频（3）

同E.3.9中考题9的式（E.31）～式（E.33），其参数改变为

A=10 m/s2，α=3 s-1，T=1 s，f0=0.1 Hz，fn=100 Hz

图E.7　等幅扫频（1）加速度时程

图E.8　等幅扫频（2）加速度时程

加速度扫频时程如图E.9所示。

E.3.12 考题12——人工随机信号

式（E.1）与式（E.7）适用于随机信号的积分处理方法，加速度a（t）可用人工随机信号表示：

图E.9　等幅扫频（3）加速度时程

式中，ωk=2πfk；φk为0～2π内的随机数；Δf=（fH-fL）/N为中心频率fk的带宽，fH为进行FFT所设置的高端频率值，fL为进行FFT所设置的低端频率值（可取fL≡0）；fk≡fL+）Δf。

速度v（t）和位移d（t）可按式（E.9）和式（E.10）得到。

人工随机信号表达式a（t）是否正确，可按如下方法验证。

随机信号功率谱密度函数G（f）的傅里叶变换的自相关函数为

而R（τ）的定义为

将式（E.35）代入式（E.38）后整理可得

当τ=0时，R（τ）则为

比较式（E.37）、式（E.38）和式（E.40）可知

离散化表示为

式（E.41）的含义为随机信号a（t）的均方值，如R（0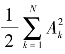）、与频域上）Δf值相等的话，则可验证功率谱密度G（f）反演后的时程式（E.35）所表征的a（t）是正确的。

［例］ 带宽的白噪声（见图E.10）

图E.10　带宽白噪声功率谱密度

设：G0=1（m/s2）2/Hz

f1=10 Hz

f2=100 Hz

B=f2-f1=90 Hz

其相关函数R（τ）理论解为

R（0）=G0B=90（m/s2）2

对应的自相关函数如图E.11所示。

图E.11　对应的自相关函数

由式（E.35）得到的加速度时程a（t）按式（E.41）求时程均方值是否满足下式的要求。