D.3.1 固体动力学基本方程

假设固体质点运动位移十分小，可忽略大变形的非线性项，则其弹性位移表征的动力学方程可表示为式中，u为质点位移矢量，u=uxi+uy j+uzk；ρs为固体密度；λ，μ分别为拉梅弹性系数，λ=　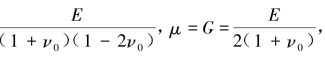，E，ν0分别为弹性模量和泊松比；G为剪切模量。

质量力为

Fs=Fsxi+Fsy j+Fszk

（D.23）

当只考虑重力场加速度g时，

Fs=gk

（D.24）

应力分量σij与应变分量εij在小形变条件下的关系为

σij=λdiv u（δij）+2μεij

（D.25）(www.daowen.com)

应变为

式中，δij=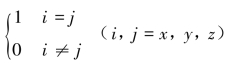　

D.3.2 相似关系推导

方程式（D.22）中有7个参量：位移、尺寸、时间、质量力、弹性模量、密度和泊松比。实物与模型之间的比例关系设为Cu，Cl，Ct，CFs，CE，Cv0，Cρ s。如模型试验中的质点波动和实物中固体运动相似，必须使模型和实物的固体元运动和本构关系均满足式（D.22），则可得到

由上式整理后可得到两个基本相似关系，其物理意义为：

（1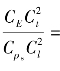），该准则表征相应固体微元的弹性力与非定常运动惯性力1的比值相等。

（2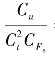）=1，该准则表征相应的固体微元非定常运动的惯性力和质量力CFs的比值相等。

由此可得到两个相似准则：

由于固体中声音传播速度cs=，所以

式中，f为频率参数，满足Cf=（Ct）-1。