D.2.1 流体动力学基本方程

假设为牛顿黏性流动的流体，其基本N-S动力方程为

其流体质量平衡方程为

式中，V=Vxi+Vy j+Vzk，Vx，Vy，Vz分别为流体微元在坐标x，y，z 3个方向（i，j，k）上的速度；P为流体微元的总压力；Ff=Fxi+Fy j+Fzk，Fx，Fy，Fz为流体微元在坐标x，y，z 3个方向（i，j，k）上的质量力，当只考虑流体微元在重力加速度g下的质量力时，Ff=gk；ρf，νf为流体密度和运动黏性系数；t为时间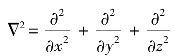；为拉氏算子；gradP=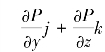为梯度；divV=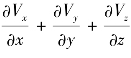为散度。

D.2.2 流体动力学方程的分解

根据流体运动的特征，流体动力学方程中的流体微元在理论上可假设为两部分：

（1）总体平均流动状态下假设为不可压缩的黏性流体微元。

（2）流体流动状态（或不流动）下假设为可压缩、无黏性的微幅波动微元。

第（1）部分流体微元类似流体流动作用在固体表面上的湍流、漩涡脱落压力脉动、液体的晃动或波浪运动。第（2）部分流体微元表征为在流体中传播的声波动，其波动假设为微幅脉动。

在式（D.1）中流体微元速度V和压力P可分解为平均流动微元和微振幅微元两部分，即

由于波动速度v和压力p是附加在平均流体速度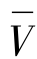 和压力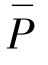上的一个小量，即

将式（D.3）代入式（D.1）和式（D.2），考虑到式（D.4）的假设条件，并略去高阶小项后可得到

（1）流体总体平均微元运动方程和质量平衡方程为

（2）流体微元质点波动方程为

对于方程式（D.6）中假设小振幅波动的可压缩条件可满足：

式中，cf为声波在流体中传播的速度，K为流体微元体积压缩模量，则式（D.7）可转化为

代入式（D.6）中的第2式得

对式（D.6）中的第1式微分后，忽略高阶小项得到

式（D.10）与式（D.5）组成流体运动与波动相耦合的方程。(www.daowen.com)

如在无流动条件下则为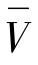≡0，方程（D.10）可退化为通用的声波动速度v所表示的方程：

或者用波动压力p表示的方程：

D.2.3 相似关系的推导

1）流体总体平均微元运动

针对流体流动方程（D.5）中共有7个基本量：平均速度、尺寸、时间、质量力、压力、密度和黏度。实物与模型之间的比例关系设为相应的Cl，Ct，CFf，CP，Cρf，Cνf。如模型试验中的流体运动和实物中流体运动相似，则必须使模型和实物的流体微元均满足式（D.5），将7个基本参数代入式（D.5）后，可得到

由上式整理后可得到4个基本相似准则，其物理意义为：

（1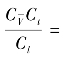）1，该准则表征相应流体微元牵连运动的相对惯性力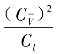和非定常绝对惯性力的比值相等，通常称为斯特劳哈尔数。

（2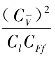）=1，该准则表征相应的流体微元牵连运动的相对惯性力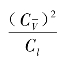和质量力CFf的比值相等，通常称为弗劳德数。

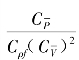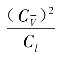（3）=1，该准则表征相应的流体微元的压力和相对惯性力的比值相等，通常称为欧拉数。

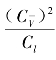（4）=1，该准则表征相应流体微元相对惯性力和黏性力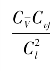的比值相等，通常称之为雷诺数。

2）流体质点波动

针对流体质点波动方程式（D.10）中有5个基本量：平均流速波动流速v、尺寸L、时间t和声速cf。如模型试验中的流体波动和实物中流体波动相似，则必须使模型和实物的流体微元均满足式（D.10），将5个基本参数代入式（D.10）后，可得到

由上式整理后可得到2个基本相似准则：

（1）=1，该式与式（D.14）完全相同，即为斯特劳哈尔数。

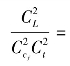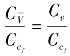（2）1，如满足全相似Cv=1条件下则得到：Cv=CL/Ct关系，该式可变换成条件，即通常称之为马赫数。

汇总式（D.14）～式（D.17）和式（D.19）、式（D.20）后可得到流体运动和波动共5个相似准则：

若要在模型试验中都满足式（D.21）所有的相似准则是十分困难的，但可根据试验的要求，选择主要的相似准则给予满足，对于次要的相似准则给予放宽。