反应谱是一族理想化的线性、单自由度、有阻尼所组成振动子上求得的最大反应曲线，其反应可包括加速度、速度或位移。该最大反应曲线反映了当振子在其对应楼面处有特定的地震运动输入时，建立一族楼面反应与振动子自然频率（或周期）的函数关系。

图B.1　单自由度振子模型

单自由度振子模型由质量m、弹簧刚度k与阻尼c组成（见图B.1），其基础输入为运动的位移x（t），其振子质量上输出运动位移为z（t）。其动力平衡方程为

设z（t）相对于基础的相对位移y（t）为

y（t）=z（t）-x（t）

（B.2）

代入式（B.1）后得相对位移y（t）下的动力平衡方程为

令ω0=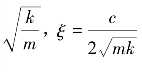(www.daowen.com)

式（B.3）可转化为

式中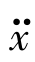，为基础上输入的加速度时程，ω0为振子的无阻尼自振圆频率（或称自然圆频率），ξ为振子的阻尼比。

并设初始条件t=0时的相对位移和速度为

由此振子动力方程式（B.4）可求得含初始条件的通解以及从方程右端求得其特解，经整理后表示为

直接利用式（B.4），振子质量上求得的绝对加速度可表示为

在t时刻上取绝对加速度的最大峰值的绝对值为再以振子的自然圆频率ω0（或f0）和阻尼比ξ为自变量，作出与ω0和ξ的函数关系曲线，可定义为绝对加速度反应谱A（ω0，ξ）：

实际上，A（ω0，ξ）就是表征当地震加速度输入时的单自由度体系反应的最大值，作为该体系的阻尼和固有频率的函数而求得反应谱来判断设计抗震能力。